这是一篇关于回溯算法的详细的入门级攻略(真的就只是入门级)。
一定要看最后的总结呀~
# 回溯的含义
回溯本质上是搜索的一种方式,一般情况下,该搜索指深度优先搜索(dfs)。且实现上使用递归的方式。
# 从 “全排列” 开始
全排列是回溯最经典的应用之一,我们以全排列做基本示例,先来理解最简单的回溯是如何执行的。
# LeetCode 46. 全排列
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入样例
3
输出样例
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1解释:输入样例为输入的整数 n。输出样例为 1~n 的三个数字 (1,2,3) 的所有排列方式。
# 简单的思路
先把这道题当做脑筋急转弯,我们很容易就可以想到简单的思路:分别把不同的数字放到每个位置上。
例如:
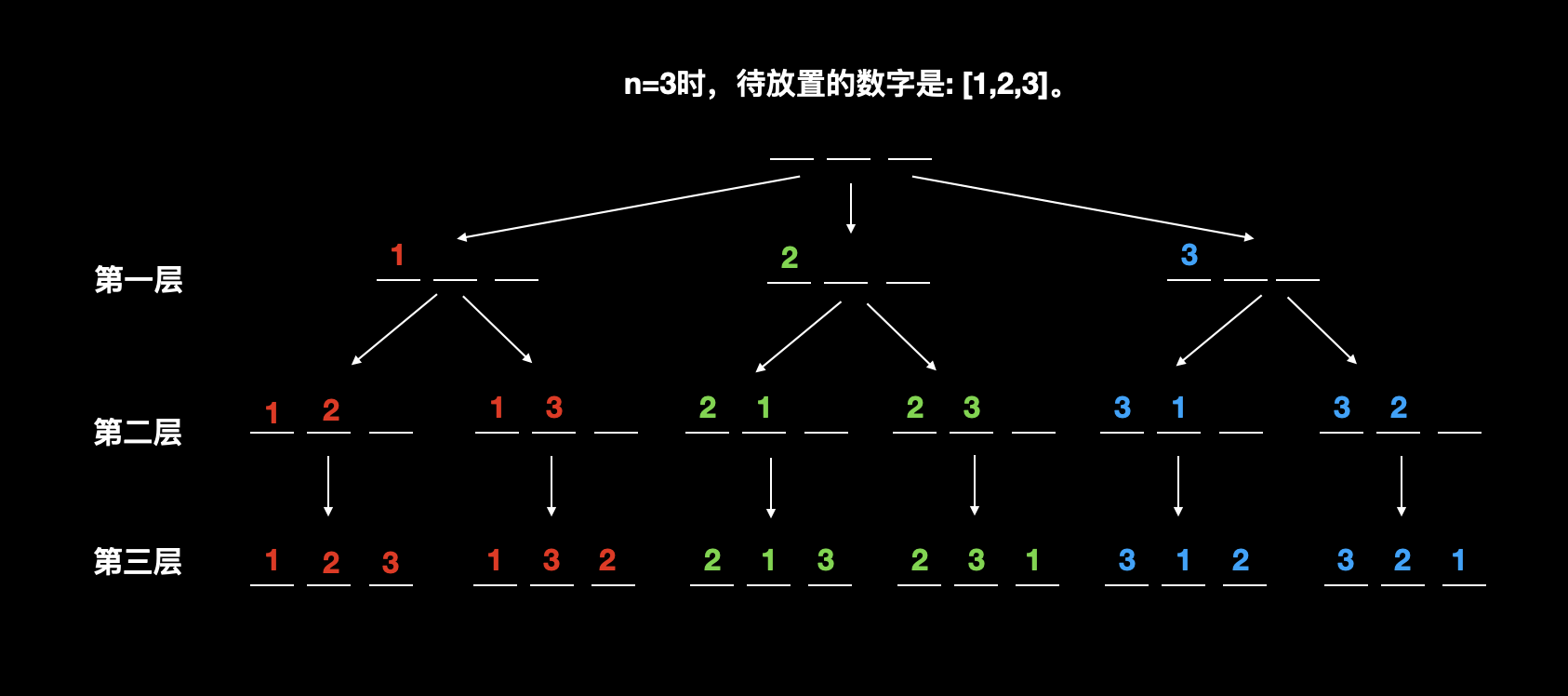
1 2 3,总共三个数,所以有三个位置,我们把1放在第一个位置,那么第二个位置可以放2或3,无论第二个位置放哪一个,第三个位置都只能放另外一个,而当三个位置都放完就找到了一个完整的排列方法;- 以此类推的,如果第一个位置放 2,那么第二个位置有两种放置方式;
- 如果第一个位置放 3,那么第二个位置同样有两种放置方式;
- 我们把这一放置的过程用可视化图形表达出来,会形成一种树的形式:
![]()
# 回溯是在做什么?
请仔细研究一下上面的放置思路,其中有一个隐藏的关键点:从第一层向下搜索到第三层,找到一个结果之后,需要重新回到第一层;再从第一层延伸到第二层的其他分支。 也就是说,需要沿着如下图的红色箭头指向顺序搜索。
想要用代码实现这一搜索过程,这一关键点是需要想清楚的:如何在搜索出一个结果之后,让代码可以往回搜索呢?
# Code
往回搜索其实就是回溯的过程,先来看下全排列中的代码实现:
class Solution { | |
public: | |
vector<vector<int>> res; // 存储所有排列方法 | |
vector<bool> st; // 存储数字是否被用过 | |
vector<int> path; // 存储当前排列方法 | |
// 使用递归的实现搜索,其中 u 表示当前已经排列的个数 | |
void dfs(int u, vector<int>& nums) { | |
// 如果已经排列的数字个数和总数字个数相等,说明已经完成一次排列 | |
// 把当前的排列方法放入最终结果,并 return。 | |
if (u == nums.size()) { // ① | |
res.push_back(path); // ② | |
return; // ③ | |
} | |
// 枚举数字 | |
for (int i = 0; i < nums.size(); i ++ ) { // ④ | |
// 没有使用过的数字参与排列 | |
if (!st[i]) { // ⑤ | |
path.push_back(nums[i]); // ⑥ | |
st[i] = true; // ⑦ | |
dfs(u + 1, nums); // ⑧ | |
st[i] = false; // ⑨ | |
path.pop_back(); // ⑩ | |
} | |
} | |
} | |
vector<vector<int>> permute(vector<int>& nums) { | |
for (int i = 0; i < nums.size(); i ++ ) st.push_back(false); | |
dfs(0, nums); | |
return res; | |
} | |
}; |
接下来是本文重中之重,我们来看一下上面的代码的完整的执行流程,以此来了解为何这样写就能完成回溯。
- 首先,要明确的几个关键角色:
u: 可以理解为 “目前使用了几个数字”、“目前处于树的第几层” 等等;res: 保存最终结果(所有路径);path: 保存当前的路径,保存的是值,比如 nums [0],nums [1] 等;st(state): 存储数字是否被使用过,上面代码直接存储的下标(也可以存储值),因此下面分析中 st 也是以下标为准;nums: 数组,既保存需要排列的数字,如n=3,nums=[1,2,3]。
- 明确递归函数的含义,递归函数最重要的就是其表达的含义,而在上面代码中,递归函数 dfs 的含义是深度优先搜索,当搜索到一个结果之后,就把结果加入到结果 res。
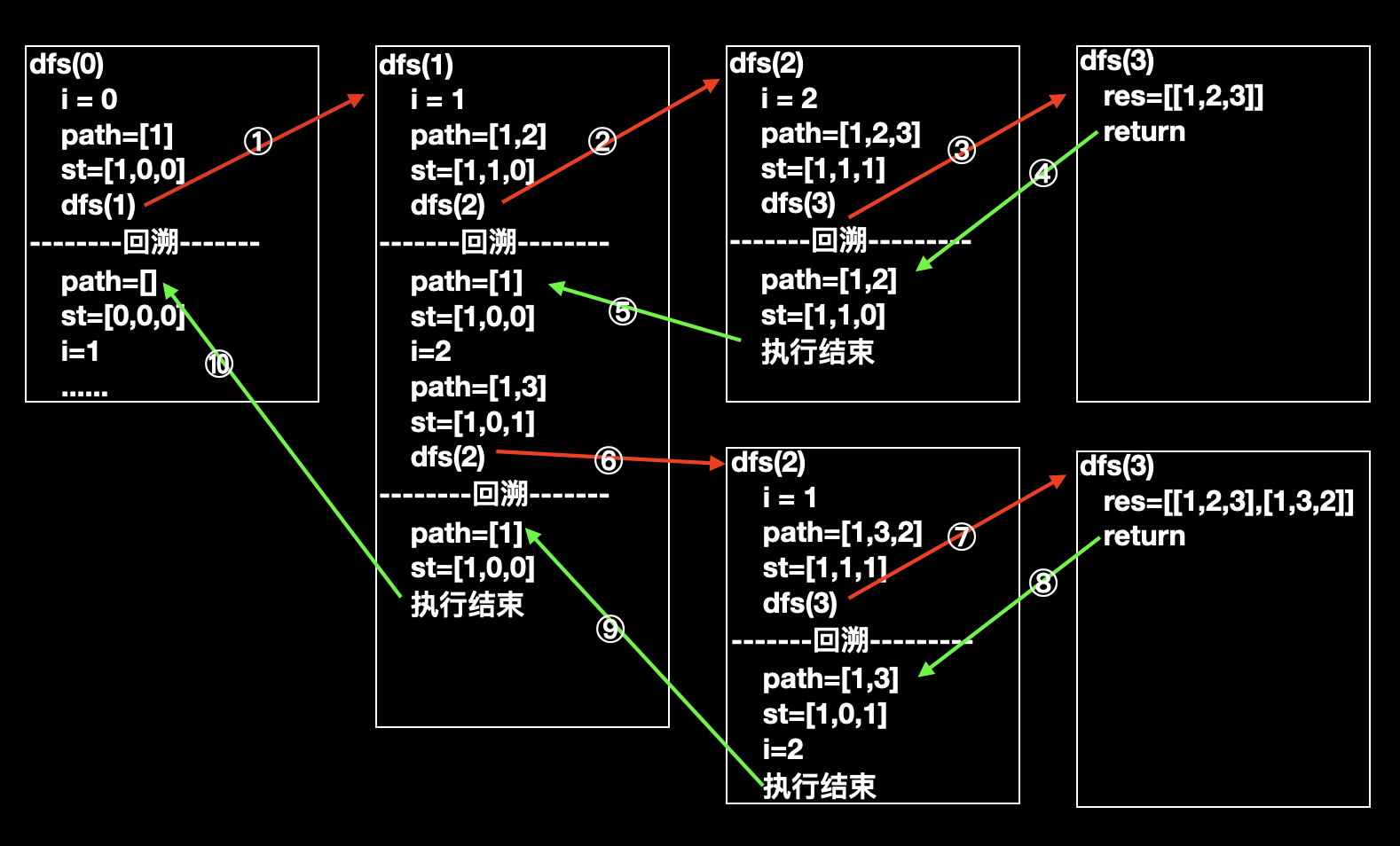
- 最最最最重要的,我们来看一下回溯的执行过程:











最最最最重要的,执行过程中的全部变化如下:
![]()
从图中 path 的变化,可以明显的看出,其实代码的执行顺序正好对应了上面图中的搜索顺序。
理解回溯(或者说递归),至关重要的一点:当一个函数让出执行权后,执行权又重新回来,函数当前的变量状态应该和让出前一致。
以上面的 dfs (1) 为例,在第 ② 步 (不是代码 ②),递归到 dfs (2) 时候 dfs (1) 的变量
i的值是 1,那么在第 ⑤ 步回到 dfs (1) 的时候,dfs (1) 的变量i的值仍然是 1,并且从 ** 递归处(代码 ⑧)** 继续向下执行。
# 总结个 “板子”
根据上面 “全排列” 的解法,我们可以总结出一个回溯问题的通用思路,下面用伪代码来描述:
res; // 存放结果 | |
path; // 存放当前的搜索路径 | |
st; // 判断元素是否已经被使用 | |
//u 表示递归处于哪一层 | |
void dfs(u) { | |
if 结束条件 { | |
res.push_back(path); | |
return; | |
} | |
for 循环 { | |
// 剪枝 | |
// do something~~ | |
dfs(u + 1); // 递归,进入下一层 | |
// 回溯,撤销 do something~~ | |
} | |
} |
下面我们就用这种方法,来批量的解决一堆回溯相关问题。
# 使用 “板子” 解决同类型题目
充分理解回溯的思路,那么就可以扩展到相同类型的题目上。
# LeetCode 47. 全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
# 思路及实现
全排列的经典扩展,给出的序列 nums 可能包含重复的,那么就需要考虑一个问题:如何避免重复数字换序后,计算为新的排列方式。
其实解决的办法很简单:跳过重复的数字。
举个例子:当前 nums 为 [1,1,2],为了便于观察我们给重复的 1 做上标记来进行区分,得到 ,那么就会出现 , 是同一种排列。
为了避免这种情况,以最左边的 为准,如果出现重复的就跳过去,那么当排列出 ,就不会再排列出 。
# Code
实现上还有一个小细节需要注意下,给出的 nums 可能是乱序的,所以要先排序一下,以方便跳过相同的数字。
因为是搜索的全排列,所以排序不会对结果产生影响。
class Solution { | |
public: | |
vector<vector<int>> res; | |
vector<int> path; | |
vector<bool> st; | |
vector<vector<int>> permuteUnique(vector<int>& nums) { | |
sort(nums.begin(), nums.end()); | |
st = vector<bool>(nums.size()); | |
// path = vector<int>(nums.size()); | |
dfs(nums, 0); | |
return res; | |
} | |
void dfs(vector<int> &nums, int u) { | |
if (u == nums.size()) { | |
res.push_back(path); | |
return; | |
} | |
for (int i = 0; i < nums.size(); i ++ ) { | |
if (!st[i]) { | |
// 剪枝。如果出现重复数字,并且重复数字已经被用了,就跳过。 | |
if (i && nums[i - 1] == nums[i] && !st[i - 1]) continue; | |
st[i] = true; | |
path.push_back(nums[i]); | |
dfs(nums, u + 1); | |
path.pop_back(); | |
st[i] = false; | |
} | |
} | |
} | |
}; |
# LeetCode 39. 组合总和
给你一个 无重复元素 的整数数组 nums 和一个目标整数 target ,找出 nums 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
nums 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
# 思路及实现
初步看题目,发现与全排列高度相似,但又有些许不同:
- 元素可以重复使用;
- 结束条件不在是所有数字全部使用,而是当前路径之和为 target;
那么,实现上我们要解决的一个重要难点就是:如何让元素可以重复使用呢?
首先,为了逐步增大路径,先给 nums 排个序。
因为数字可以重复使用,所以用来判重的 st 也就没必要使用了。
最重要的是使元素重复使用,我们引入一个新的参数
start,它表达的含义是每次递归从 start 开始搜索。这样有什么效果?举个例子就清晰了,我们当前枚举到了 i=2,那么我们把
i当作参数start传到下一层,下一层又会从start开始枚举,不就重复使用 i=2 了嘛?请读者将上面,加粗的描述多读几遍,细细体会一下
start是如何解决本题最大难点的。st 与 start 的区别是什么?或者说分别在什么时候使用?
在全排列中,因为每个数字只能使用一次,所以我们用了 st 数组,把使用过的数字标记一下,这样在下一层遇到的时候,就可以跳过使用过的。
例如:当前
i=0,st=[1,0,0],下一层重新从0枚举到3,当枚举到0的时候,发现st中0已经被使用过了,因此跳过了0,继续循环,得到i=1。所以 st 可以用来判重。
在该问题中,因为数字可以重复使用,所以用来判重的
st显然就没有存在的必要了。而为了计算重复元素,我们引入 dfs () 的新参数 start,每次从 start 开始枚举,这样每次把当前 i 的值传给 start,那么下一层还是从当前 i 枚举的。但是这里引申出一个重要的问题:下一层递归不从 0 开始重新枚举,不会枚举不全吗?答案是:不会的,一个重要原因是提前将 nums 从小到大,排好了序,所以从较小的数开始枚举,一定是一直枚举较小的数,直到较小的数也会超过 target 或者 较小的数加起来等于 target。
这样,对于较小的数来说,我们已经全部放入了 path,较小的数的使用个数不能再增多了(只能减少),所以也就没有枚举较小的数的必要了。
举个例子:
nums = [2,3,6,7], target = 7,假设 nums 已经排序好,那么我们一定是一直枚举最小的数2,直到再枚举最小的数2也会超过 target。那就是
[2,2,2],此时下一个2会使总和超过 target,所以直接回溯,再枚举3,得到结果之一[2,2,3]。我们发现当前路径
path达到[2,2,2]时,合法路径中,能容纳的最小数 2 已经到上限了,无法再增多了,而为了配合后面比他大的数,它只能慢慢减少,直到算法结束~~总结一下,start 可以控制下一次枚举的开始位置。
把当前的思路带入到 “板子” 中,会发现实现很简单。
# Code
class Solution { | |
public: | |
vector<vector<int>> res; | |
vector<int> path; | |
vector<vector<int>> combinationSum(vector<int>& nums, int target) { | |
sort(nums.begin(), nums.end()); // 至关重要的排序 | |
dfs(nums, 0, target, 0); | |
return res; | |
} | |
//dfs 的参数多加一个 start | |
void dfs(vector<int>& nums, int u, int target, int start) { | |
// 当前路径和正好等于 target 时,说明找到了一个合法路径。 | |
if (target == 0) { | |
res.push_back(path); | |
return; | |
} | |
for (int i = start; i < nums.size(); i ++ ) { | |
// 剪枝。如果超过 target,直接开始回溯。 | |
if (target < nums[i]) return; | |
// do something~~ | |
path.push_back(nums[i]); | |
target -= nums[i]; //target 减少 | |
// 递归。注意 start 处传的参数,是当前的 i,所以下一层递归也会从这个 i 开始, | |
// 这样就达到了重复使用数字的目的。 | |
dfs(nums, u + 1, target, i); | |
// 撤销 do something | |
target += nums[i]; | |
path.pop_back(); | |
} | |
} | |
}; |
# LeetCode 40. 组合总和 II
给定一个候选人编号的集合 nums 和一个目标数 target ,找出 nums 中所有可以使数字和为 target 的组合。
nums 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
# 思路及实现
对比上一道题(组合总和),本题有两个关键点:
数字不可以重复使用
只要读者认真理解了上面一题
start的含义,想必很快就能解决这个问题 (就很快啊~)。还记得在上一道题我们讲了start的作用吗?我们为了让数字可以重复被使用,所以在start位置传了当前枚举的数字i,这样下一层枚举也会从i开始。那么显然,对于这个问题的该关键点,只要把 start 位置的传参改成i+1就可以了。结果不能出现重复
细心的小同学,可能已经发现了,“诶?这个问题不是在全排列 2 中解决过嘛?”
没错,直接把全排列 2 中的那个剪枝拿过来就可以了(“拿来” 主义狂喜~)。
# Code
为了节省码字时间和文章空间,本题就不放完整代码了,正好读者可以自己试试能不能写出来。
下面写出两个关键点的实现,其余的代码和上一题 “组合总和” 完全相同。
for 循环 { | |
// 剪枝。全排列 2 的思路:对于重复数字直接跳过就可以啦。 | |
if (target < nums[i]) return; | |
if (i > start && nums[i - 1] == nums[i]) continue; | |
// do something~~ | |
// 递归。数字不可以重复使用。 | |
dfs(nums, u + 1, target, i + 1); | |
// 撤销 do something~~ | |
} |
# LeetCode 77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
# 思路及实现
对比其它题目,本题有两个关键点:
递归结束条件,不在是排列完 n 个数,而是排列完 k 个数
解决该问题,很简单,直接换一下递归结束条件即可。
从示例中可以看出,最终结果中,数字相同的组合即便顺序不同也不能存在,比如:[1,2],[2,1] 属于一种。
这个问题其实也不难,思考一下,其中的搜索顺序是从前往后搜索,而对于已经搜索完的位置是不需要重复搜索的,注意体会上一句话,为什么搜索完的位置不需要重复搜索呢?
以
n=4,k=2为例,显然,会先搜索出由1开头的 [[1,2],[1,3],[1,4]](搜索够两个数就回溯了,比如搜索出 [1,2],就回到 [1],然后搜索出 [1,3]),现在,请注意,当我们搜索由2开头的路径的时候,不需要再搜索 [2,1] 了,同时 [2,2] 也是不合法的,因为每个数字只能用一次,也就是从2的下一个数3开始搜索就可以了。那么,如何能让递归搜索的时候,搜索下一个数呢?
很显然,这就对上了组合总和中所讲的
start的作用。
# Code
同样给出部分与其他题目不同的地方的实现,读者可以自己补充全 (好像基本也全写出来了 😅)。
void dfs(int u, int n, int k, int start) { | |
// 递归结束条件 | |
if (k == 0) { | |
.... | |
} | |
for (int i = start; i <= n; i ++ ) { | |
k -= 1; | |
path.push_back(i); | |
dfs(u + 1, n, k, i + 1); | |
path.pop_back(); | |
k += 1; | |
} | |
} | |
//dfs 函数初始化 | |
dfs(0, n, k, 1); |
# LeetCode 78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
# 思路及实现
对比其他题目,本题有一个明显与其他题目不同的关键点:
没有明显的递归终止条件
在上一道题(77. 组合)中,递归终止条件由题目给出,既 k=0 时候,递归终止。而递归终止也就意味着,把当前路径 path 放到最终结果 res 中。
而本题,没有这个条件,怎么办?选择什么样的时机把当前路径 path 放到最终结果 res 呢?
认真观察给出的示例,可以得到答案:
每次递归都把 path 放到 res
如果认真观察,我们本文中讲过的每一道题目,其实递归中止(或者叫开始回溯)的方式都有两个:
- 明显的是:满足递归终止条件之后的 return。
- 不明显的是:每当 for 循环全部执行完毕之后,递归也会终止。
而本题就要使用不明显的结束循环的方式进行回溯。
上图中的 dfs (0),表示下一次搜索的位置,也就是 start。并且从上图中也能较清晰的看出,我们把每次递归到下一层的数字都存到当前路径,自然而然的就得到了所有子集,既 [1],[1,2],[1,2,3],[1,3],[2].... 。
# Code
实现方面就非常的简单了,只要把递归结束条件去掉就行了。
void dfs(vector<int>& nums, int start) { | |
res.push_back(path); | |
for (int i = start; i < nums.size(); i ++ ) { | |
path.push_back(nums[i]); | |
dfs(nums, i + 1); | |
path.pop_back(); | |
} | |
} |
# 把 dfs 搜索扩展到其他类似题型
# LeetCode 22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
# 思路及实现
对比其他题目,本题变化就比较大了,以至于可能无法一眼看出,本题需要用回溯来搞定,这是因为我们要先找出其中括号生成的规律。
- 为了使括号合法,我们应该先生成左括号。(这看起来似乎是一句废话,却是后面规律的基础。)
- 根据题目条件:总共需要生成 n 对括号,我们可以知道左括号的生成个数小于等于 n。换一句话说,只要左括号的数量没有达到 n,我们就可以生成左括号。
- 根据题目条件:有效的括号组合,我们可以知道,右括号的数量应该总是小于等于左括号的数量。
- 综上,我们可以得到递归的终止条件:当有 n 个左括号,并且右括号的数量与左括号相等(即也是 n 个)即说明我们找到了一种组合方式。
# Code
class Solution { | |
public: | |
vector<string> res; | |
vector<string> generateParenthesis(int n) { | |
dfs(0, 0, "", n); | |
return res; | |
} | |
//l, r 分别表示左右括号数量,cur 表示当前的字符串 | |
void dfs(int l, int r, string cur, int n) { | |
// 递归结束条件 | |
if (l == n && l == r) { | |
res.push_back(cur); | |
return ; | |
} | |
// 左括号数量不够 | |
if (l < n) dfs(l + 1, r, cur + "(", n); | |
if (r < l) dfs(l, r + 1, cur + ")", n); | |
} | |
}; |
# 本题需要注意的点
为何不需要撤销操作呢?
注意看,我们选择路径用的是 cur 并非是全局变量,而是每个函数的独有参数。
例如:当我们递归到 dfs (2, 0, "((", n) 的时候本层的参数 cur 就是 "((",这是已经固定的,等我们在回溯到第二层的时候,cur 依旧是 "(("。
本题使用的依旧是不明显的回溯方式,即循环结束回溯。
本题通过最后一行代码进行递归,所以回溯的时候,也是连续回溯的。即:“((()))” 会直接回溯到 “((” 才开始下一轮递归。
因为当 “((()))” 回溯到 “((())” 的时候,会发现 “((())” 对应的函数也执行结束了,那么就会又回溯到上一层,直到回溯到一个没有直接执行结束的函数,从这个函数开始下一轮递归。
# LeetCode 200. 岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和 / 或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
# 思路及实现
乍一看这题好像和前面的题没有什么关系,但其实理解题意后会发现,这也是一道搜索题目。
首先理解一下本题的题意:
横竖连接起来的 1 (陆地) 表示岛屿(斜着不行),而 0 表示海水,问有多少个岛屿。
通过示例来看,其实就是问由 1 横竖连接起来的块有几个,示例中是 1 个,既,如下图所示。
那么,如何来进行判断呢?通过本小节的标题,其实读者应该也能判断出来,主要还是按照顺序搜索。
具体的:
- 我们从左上角开始搜索,遇到 1 就说明找到了一个岛屿,并且开始 dfs。
- dfs 时向四个方向扩展,而可以扩展到的 1,就说明是与当前岛屿是一体的,因此把他们变成海水(0),避免 组成当前岛屿的陆地 被重复搜索。
- 用这种搜索方式,我们就可以找到所有的岛屿。
# Code
class Solution { | |
public: | |
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1}; | |
int numIslands(vector<vector<char>>& grid) { | |
int res = 0; | |
int n, m; | |
n = grid.size(), m = grid[0].size(); | |
for (int i = 0; i < n; i ++ ) { | |
for (int j = 0; j < m; j ++ ) { | |
if (grid[i][j] == '1') { | |
res ++ ; | |
dfs(i, j, grid); | |
} | |
} | |
} | |
return res; | |
} | |
void dfs(int x, int y, vector<vector<char>>& grid) { | |
int n, m; | |
n = grid.size(), m = grid[0].size(); | |
grid[x][y] = '0'; // 搜索过的陆地变成海水,防止再搜索 | |
// 向四个方向搜索 | |
for (int i = 0; i < 4; i ++ ) { | |
int a = x + dx[i], b = y + dy[i]; | |
// 跳过出界的格子 | |
if (a < 0 || a >= n || b < 0 || b >= m) continue; | |
// 跳过海水 | |
if (grid[a][b] == '0') continue; | |
// 向下搜索 | |
dfs(a, b, grid); | |
} | |
} | |
}; |
# LeetCode 51. N 皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]解释:如上图所示,4 皇后问题存在两个不同的解法。
# 思路及实现
n 皇后问题,也是特别经典的回溯问题,我可以按行进行搜索,对于每一行的每个格子,都判断它能不能放棋子。
# 用全排列的思路进行分析
请注意,这个搜索场景是不是和基础的全排列十分相似呢?
全排列中按照 每个数字 进行搜索,用每个数字和剩下的数字排列。
而 n 皇后用 行 进行搜索,对每行的每个格子都判断是否能放棋子。
而两题的区别也是比较明显的:
- 在全排列中非重复的数字就可以被扩展到,因此我们用一个数组 st 来存储数字是否被用过;
- 而在 n 皇后中需要这个格子的所在列以及所在正反对角线没有皇后才可以扩展到,这就意味着我们需要三个用来判重的数组,分别存储当前格子所在列及正反对角线是否被占用,以此来判断当前格子能不能放棋子;
进一步分析,就来到了本题最难的点:如何放置一个棋子之后,把该棋子的正反对角线也全部置为已经占用呢?
要解决这个问题,我们先看一下对于某一列是如何置为被占用呢?
直接用一个判重数组 (col) 就可以了,比如:col [1],就表示第二列已经被占用了,假设当前是第 3 行,下次递归到第 4 行,在第 4 行判断第二列的时候,也要用 col [1],发现已经是 true,既被占用。
用伪代码表示这一过程:
vector<bool> col; | |
dfs(u) { | |
for (int i = 0; i < n; i ++ ) { | |
col[i] = true; | |
dfs(u + 1); | |
} | |
} |
到了对角线这里,可以使用 行坐标+列坐标(即u+i) 来判断对角线位置是否被占用,我们把棋盘放在坐标系上: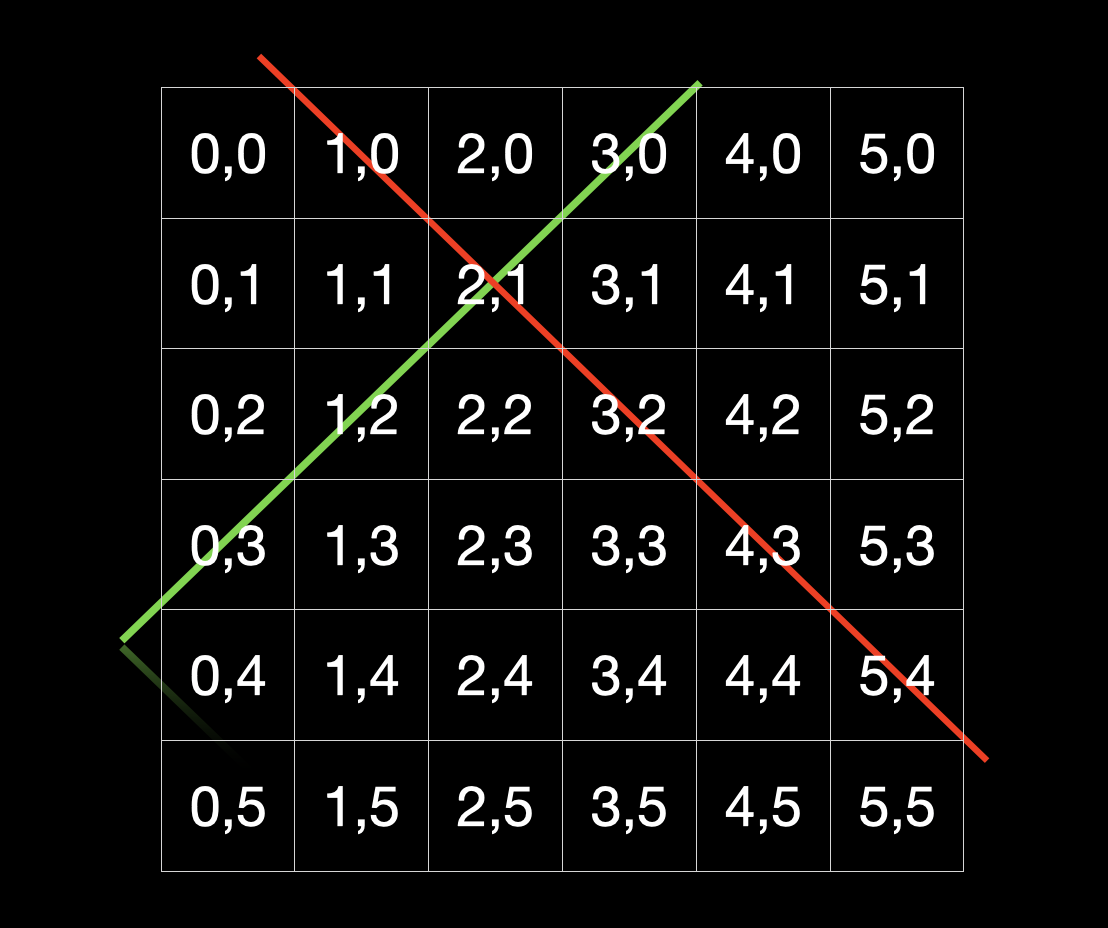
当我们选择点 x (2,1) 放棋子的时候,那么它的两条对角线就不能再放了,用红绿色线标识过点 x 的两条对角线,可以直观的看到其中绿色对角线的横纵坐标之和总是相等的;而红色对角线的坐标之差总是相等的。
然后把三个判重数组带入到板子中,替换掉 st 数组。
# Code
class Solution { | |
public: | |
vector<vector<string>> res; | |
vector<string> path; | |
vector<bool> col, dg, udg; | |
int n; | |
vector<vector<string>> solveNQueens(int _n) { | |
n = _n; | |
col = vector<bool>(n); | |
dg = udg = vector<bool>(n * 2); | |
path = vector<string>(n, string(n, '.')); | |
dfs(0); | |
return res; | |
} | |
// 其中 u 表示枚举 行 | |
void dfs(int u) { | |
// 结束条件 | |
if (u == n) { | |
res.push_back(path); | |
return ; | |
} | |
// 循环 列 | |
for (int i = 0; i < n; i ++ ) { | |
// 判重 | |
if (!col[i] && !dg[u + i] && !udg[u - i + n]) { | |
path[u][i] = 'Q'; // 放棋子 | |
// 其中 u-i+n 是为了避免出现负数,其中 n 是多少无所谓。 | |
col[i] = dg[u + i] = udg[u - i + n] = true; | |
dfs(u + 1); // 递归 | |
// 回溯 | |
col[i] = dg[u + i] = udg[u - i + n] = false; | |
path[u][i] = '.'; | |
} | |
} | |
} | |
}; |
# AcWing 165. 小猫爬山
翰翰和达达饲养了 N 只小猫,这天,小猫们要去爬山。
经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了(呜咕 >_<)。
翰翰和达达只好花钱让它们坐索道下山。
索道上的缆车最大承重量为 W,而 N 只小猫的重量分别是 C1、C2……CN。
当然,每辆缆车上的小猫的重量之和不能超过 W。
每租用一辆缆车,翰翰和达达就要付 1 美元,所以他们想知道,最少需要付多少美元才能把这 N 只小猫都运送下山?
输入格式
第 1 行:包含两个用空格隔开的整数,N 和 W。
第 2..N+1 行:每行一个整数,其中第 i+1 行的整数表示第 i 只小猫的重量 Ci。
输出格式
输出一个整数,表示最少需要多少美元,也就是最少需要多少辆缆车。
数据范围
1≤N≤18,
1≤Ci≤W≤10^8
# 思路及实现
先来看下基本的题意:有 n 只小猫重量是 Ci,有称重量为 W 的缆车,问我们要用多少辆缆车,才能装下所有的小猫。
从本题的数据范围来看,N 特别小而 Ci 和 W 特别大,所以使用回溯枚举出所有搜搜方式来解决。
而搜索问题,我们就要考虑搜索顺序了。
从题意上来看,对于每只小猫咪都可能有两种决策:
如果不会超重,就可以放到一个已有的缆车里,递归放下一只猫咪;
如果已有缆车都不能放,选择一辆新的缆车,递归放下一只猫咪;
使用这两种放置方式,最终我们会枚举出所有的放置方式,自然也就能找到使用缆车最少的那种方式。
接下来,我们如何找到使用最少缆车的方案呢?
(为了区分递归中的过程和结果,下面把搜索过程中产生的方案称为路径,把所有猫咪全安排好后的产生的结果称为方案,每个方案都是使用的缆车数。)
可以把 “使用缆车个数” 作为递归参数,每次在递归的时候判断如果当前路径大于等于当前最优方案,那么就可以直接回溯了,这样当我们枚举完所有猫咪,如果还没回溯,当前路径自然就是新的最优方案了。
请注意,既然在第二步已经设置了剪枝:大于当前最优方案直接回溯,那么我们可以进行进一步剪枝,既把猫咪按照重量从大到小排序。
思考一下,为什么可以这样呢?在最初的全排列中,我们就已经知道不断的递归回溯,最后会形成递归树,而树的分支越少就证明搜索的越快。
那么当我们设置了,当前路径大于等于当前最优方案就回溯的时候,我们只要按照最大重量的猫咪开始搜索,这样占用的缆车承重就是比较大的,所以剩余的承重就变小了,可选择的猫咪也就变少了,树的分支也就变少啦~
# Code
#include <iostream> | |
#include <algorithm> | |
using namespace std; | |
typedef long long LL; | |
const int N = 20; | |
int cat[N], sum[N]; //sum 存储每个缆车的重量 | |
int n, w; | |
int res = N; | |
void dfs(int u, int k) { | |
// 当前路径大于等于当前最优方案, | |
// 没必要再搜索了直接回溯 | |
if (k >= res) return ; | |
// 搜索完所有小猫咪而没有回溯 | |
// 当前方案则比最优方案更好。 | |
if (u == n) { | |
res = k; | |
return ; | |
} | |
// 枚举每辆缆车,注意这里枚举的是缆车,而不是猫咪。 | |
for (int i = 0; i < k; i ++ ) { | |
// 如果说放当前猫咪不会超重,就放到缆车 i。 | |
if (cat[u] + sum[i] <= w) { | |
sum[i] += cat[u]; | |
dfs(u + 1, k); | |
sum[i] -= cat[u]; | |
} | |
} | |
// 新开一个缆车, | |
sum[k] = cat[u]; | |
dfs(u + 1, k + 1); | |
sum[k] = 0; | |
} | |
int main () { | |
cin >> n >> w; | |
for (int i = 0; i < n; i ++ ) cin >> cat[i]; | |
sort(cat, cat + n); | |
reverse(cat, cat + n); | |
dfs(0, 0); | |
cout << res << endl; | |
return 0; | |
} |
# 总结
回溯问题的本质就是一种全搜索,我们一般称之为爆搜,简言之就是暴力的搜索出所有可能的情况,从而找到一种需要的结果。
我们在基础例题全排列中,给出了一个较为通用的模板,在实际应用当中,读者应熟练应用该模板,根据不同的题目灵活完成模板的每个步骤。比如:
- 全排列中要求每个数字不能重复使用,我们就使用一个数组来进行判重;
- 组合总和中数字可以重复使用,就用 start 参数来做标记,每次从上一层最后被搜索的数字开始搜索;
- 组合中要求 k 个数字的不同组合,因此在递归结束条件中,只要搜索到 k 个数,就开始回溯;
- 括号生成中的搜索使用了 “不明显的回溯”,即函数执行结束回溯;
- 岛屿数量中因为只需要一路向下搜索(递归),搜索完整个图就可以了,而不需要回溯。
- N 皇后是非常经典的题目,根据其规则,我们要把判重数组扩充到三个;
- 小猫爬山中至关重要的是搜索的顺序以及剪枝;
另外,回溯的时间复杂度一直没有提到,这是因为回溯问题因为要搜索出所有可行的方案,所以时间复杂度很高,会达到 O (n!),而通过不同的剪枝,又会极大降低时间复杂度,因此回溯问题的时间复杂度会随着剪枝和数据范围的变化而变化。
但是,可以肯定的是,因为基础时间复杂度很高,所以需要使用回溯的问题数据范围一般都很小,读者可以关注一下上面题目中的数据范围,例如:小猫爬山的 N 只有 18。
也因此,当遇到数据范围较小的问题时,我们可以考虑一下是否可以使用回溯,暴力的求出所有可能的方案,从其中找到答案。
面对回溯问题,我们一般需要考虑的是:
- 确定递归结束的条件(何时开始回溯?)
- 通过什么样的顺序搜索?
- 是否需要回溯(考虑是否使用了全局变量更新状态)?
- 是否需要剪枝?
- 前面四步考虑清楚,尝试着带入到模板就可以啦~~
ENG