首页 算法 数学

# 组合数

从 n 个不同元素中取出 k 个元素的所有不同组合的个数，叫做从 n 个不同元素中取出 k 个元素的组合数，记做：CnkC_{n}^{k} 。

从 n 个元素取出 k 个元素，用公式表示可以写为：Cnk=n!k!(n−k)!C_{n}^{k} = \frac{n!}{k!{(n-k)!}} 。

# 问题

给定 n 组询问，每组询问给定两个整数 a，b，请你输出 Cabmod109+7C_{a}^{b} \bmod 10^9+7 的值。

对于该问题可能会有不同的数据范围，但是无论那种数据范围，肯定不能直接用阶乘求，不然很容易就会超时。

# 数据范围较小

具体的：
1 ≤ n ≤ 10000,
1 ≤ b ≤ a ≤ 2000

该范围下，可以使用类似动态规划的思路。从定义进行分析，其中CnkC_{n}^{k} 表示的从 n 中选出 k 个，很容易可以想到，如果我们枚举每个 n 中的数，那么对于当前数，都有两种可能性 。

  1. 选择当前数。那么，我们已经选出了 k 中的一个数，此时 k 剩下 k-1 ，而 n 因为遍历了一个数，所以总数还剩下 n-1 。所以最后变成了Cn−1k−1C_{n -1}^{k - 1} 。
  2. 不选当前数。那么，因为已经遍历了当前数，所以总数还剩下 n-1 个。而当前数没有被选择，所以需要选择的 k 个数，还是 k 个不变，所以最后变成了Cn−1kC_{n-1}^{k} 。

如果直接从动态规划的思路来看，就是：

  1. 状态定义：使用 C(i,j) 表示从 i 个数中选出 j 个的所有方案数。
  2. 状态转移：对于当前的第 i 个数，有选和不选两种情况，如果选就是从 C(i-1, j-1) 转换而来，不选就是从 C(i-1,j) 转换而来。

# 举例

在 10 个苹果中选择 2 个，问有几种方案呢？

这时候，如果我们遍历所有的 10 个苹果。那么对于第一个苹果，无论选不选，苹果总数都剩下 9 个；而如果选择了这个苹果，那么还需要被选择的就剩下了一个，如果不选，还需要被选择的就依然是两个。

# Code

输入样例：
3
3 1
5 3
2 2
输出样例：
3
10
1

在这种做法下，我们需要两层遍历，所以时间复杂度是O(n2)O(n^2) ，也就是 10610^6 。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2010, mod = 1e9 + 7;
int c[N][N];
int init() {
    for (int i = 0; i < N; i ++ ) {
        for (int j = 0; j <= i; j ++ ) {
            // 当没有需要选择的数字是，本身就是一种方案；
            if (!j) c[i][j] = 1;
            // 状态转移方程；
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
        }
    }
}
int main() {
    init();
    int n;
    scanf("%d", &n);
    while (n -- ) {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", c[a][b]);
    }
    return 0;
}
# 数据范围提高
具体的：
1 ≤ n ≤ 10000,
1 ≤ b ≤ a ≤ 100000
该范围下，O(n2)O(n^2) 的时间复杂度会超时，因此需要换种解法，通过公式来解。
还记得公式是由阶乘组成的吗？阶乘最后的结果是比较大的数，而大数的除法操作是非常不方便的，因此可以考虑使用逆元把除法变成乘法。
再回顾下组合数公式：Cnk=n!k!(n−k)!C_{n}^{k} = \frac{n!}{k!{(n-k)!}} 。
假设 fact[i] 为i!mod109+7i! \bmod 10^9+7 ； infact[i] 为(i!)−1mod109+7(i!)^{-1} \bmod 10^9+7 ，即 i 的阶乘的逆元。
那么我们就能把除法转换为乘法逆元，即：n!k!(n−k)!=fact(n)∗infact(n)∗infact(n−k)\frac{n!}{k!{(n-k)!}}=fact(n)*infact(n)*infact(n-k)
因为模数109+710^9+7 是质数，所以我们可以根据费马小定理，用快速幂求出逆元。
# Code
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9+7;
int fact[N], infact[N];
// 快速幂
int qmi(int a, int k, int p) {
    int res = 1;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}
void init() {
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i ++ ) {
        fact[i] = (LL)fact[i - 1] * i % mod; // 求阶乘
        // 阶乘 快速幂求逆元
        infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
}
int main() {
    init();
    int n;
    scanf("%d", &n);
    while (n -- ) {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", (LL)fact[a] * infact[a - b] % mod * infact[b] % mod);
    }
    return 0;
}
# 数据范围较大
给定 n 组询问，每组询问给定三个整数 a,b,p，其中 p 是质数，请你输出 CabmodpC_{a}^{b} \bmod p 的值。
数据范围：
1≤n≤201\le n \le 20,
1≤b≤a≤10181\le b \le a \le 10^{18},
1≤p≤1051\le p \le 10^5
该范围下数据非常大，达到了101810^{18} ，因此前面两种做法不再适用。这里需要使用卢卡斯（Lucas）定理。
# 卢卡斯（Lucas）定理
对于非负整数 a,b 和质数 p，有：
Cba≡Camodpbmodp∗C[a/p][b/p](modp)C_{b}^{a}\equiv C_{a \bmod p}^{b \bmod p}*C_{[a/p]}^{[b/p]}(\bmod p)
此处应该有该公式的证明，可是我还不会。
在组合数中两个数 a 和 b 非常大且模数是质数的时候可以使用 lucas 定理。
在 lucas 中有两部分关键计算：
  1. 一部分是CamodpbmodpC_{a \bmod p}^{b \bmod p} 。因为amodp{a \bmod p} 和 bmodp{b \bmod p} 都一定是比 p 更小的数，所以我们就可以用普通的求组合数方式的方式来求。
  2. 第二部分是C[a/p][b/p]C_{[a/p]}^{[b/p]} 。因为a/pa/p 和b/pb/p 依然是比较大的两个数，那么可以继续用 lucas 定理，直到 a 和 b 小于 p。
现在问题变成了，如何计算CamodpbmodpC_{a \bmod p}^{b \bmod p} ？
在上节中，我们预处理出 1~N 中所有的数的阶乘和逆元，来实现快速求解公式，即预处理是O(Nlogn)O(Nlogn) 的时间复杂度。但是在该范围下，这个时间复杂度妥妥的超时。
因此，必须换一个方式求组合数CabC_{a}^{b}。
  1. 我们将CabC_{a}^{b} 的公式展开：
Cab=a!b!(a−b)!=a∗(a−1)∗(a−2)∗...∗(a−b+1)∗(a−b)∗...∗1(a−b)∗(a−b−1)∗...∗1∗b!C_{a}^{b}=\frac{a!}{b!{(a-b)!}}=\frac{a*(a-1)*(a-2)*...*(a-b+1)*(a-b)*...*1}{(a-b)*(a-b-1)*...*1*b!}
  1. 在上面的公式中，很明显有一个公共部分，即(a−b)∗(a−b−1)∗...∗1(a-b)*(a-b-1)*...*1 ，我们把上下的公共部分削去，剩下：
Cab=a∗(a−1)∗(a−2)∗...∗(a−b+1)b!C_{a}^{b}=\frac{a*(a-1)*(a-2)*...*(a-b+1)}{b!}
  1. 因此，我们直接递减的先乘以 a ，再除以 b ，最后如此重复 b 次即可（因为 a~a-b+1 总共 b 次计算）。
  2. 用伪代码表示：
    res = 1;
    for (int i=a, j=0; j<=b; i --, j ++ ) {
        res = res * i % p;
        // 除以 b% p 相当于乘以 b 的逆元，因为 p 是质数，所以
        // 可以用快速幂求 b 的逆元。
        res = res * qmi(j,p-2) % p;
    }
# Code
输入样例：
3
5 3 7
3 1 5
6 4 13
输出样例：
3
3
2
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
int p;
// 快速幂
int qmi(int a, int k) {
    int res = 1;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}
int C(int a, int b) {
    int res = 1;
    for (int i = a, j = 1; j <= b; i --, j ++ ) {
        res = (LL)res * i % p;
        res = (LL)res * qmi(j, p-2) % p;
    }
    return res;
}
LL lucas(LL a, LL b) {
    if (a < p && b < p) return C(a, b);
    // 直接套用 lucas 公式
    return (LL)C(a % p, b % p) * lucas(a/ p, b / p) % p;
}
int main() {
    int n;
    cin >> n;
    while (n -- ) {
        LL a, b;
        cin >> a >> b >> p;
        cout << lucas(a, b) << endl;
    }
    return 0;
}
# 数据范围不大，但是结果非常大
1≤b≤a≤50001\le b \le a \le 5000
输入 a,b，求 CabC_{a}^{b} 的值。注意结果可能很大，需要使用高精度计算。
再次回顾一下组合数的公式：Cab=a!b!(a−b)!C_{a}^{b} = \frac{a!}{b!{(a-b)!}} 。
可以看到不仅有高精度乘法还要计算高精度除法，非常的麻烦～～
因此，我们可以先分解质因数，分解质因数之后只需要用到高精度乘法。
因为我们可以用 分子(a!) 里面的 质因数P的个数 减去 分母(b!*(a-b)!) 里面的 质因数p的个数 ，剩下的就是CabC_{a}^{b} 中 质因数p的个数 。
而分母中无论是 b! ，还是 (a-b)! 都一定是小于 a! 的。所以我们只要分解出 a! 的质因数，再找到哪些质因数出现在CabC_{a}^{b} 中，最后求出出现的这些质因数的个数，把所有的质因数再乘起来就算出了最终CabC_{a}^{b} 的结果。
假设 a! 分解质因数为：p1α1∗p2α2∗p3α3∗...∗pkαk{p_1^{\alpha 1} * p_2^{\alpha 2} * p_3^{\alpha 3} * ... * p_k^{\alpha k}} 。
现在，问题来到了，如何求出 a! 分解质因数后，每个质因数 p 的个数呢？
其实就是 1~a! 中p,p2,p3,...,pkp,p^2,p^3,...,p^k 的倍数的个数。
如何理解这句话呢？我们不妨来看个例子。比如我们想求出来 12! 中有多少个质因数 2，我们不必计算出 12! 到底是多少。
  1. 首先，我们都知道其中 2、4、6、8、10、12 是 12 以内的 2 的倍数，共有 6 个。所以，目前这 6 个数各提供一个 2。
  2. 再看，数字 4 中似乎存在两个 2，我们并没有算另一个 2。所以要把另一个 2 也计算出来。并且 12 中有三个数都是 4 的倍数，也就是说除了 4 本身，还有它的 2 倍 (8)、3 倍 (12) 都可以提供第二个 2。那么此时，又多找出了 3 个 2，其中 4,8,12 各提供一个。现在是 9 个。
  3. 最后，我们知道数字 8 是 2 的三次幂，也就是说在 1~12 的所有数字中，8 可以提供出第三个 2。那么除了 8 以外还有其他数字能提供第三个 2 吗？在 12 以内是没有了，所以算上 8 提供的第三个 2，现在总共是 10 个 2。
  4. 最后总结一下，是怎么找到这 10 个 2 的。我们用 12/2 找到 6 个，又用 12/(2^2) 找到 3 个，最后又用 12/(2^3) 向下取整找到了最后一个。用通用公式表示一下这个过程就是：在 n! 中找到质因子 p 的个数的方法是:np+np2+...+npk\frac{n}{p} + \frac{n}{p^2} + ... + \frac{n}{p^k} （其中每个分数都向下取整，且pk≤np^k \le n ）。
# Code
输入样例：
5 3
输出样例：
10
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N], cnt; // 存储质数和个数
int sum[N]; // 存储最终 C (a,b) 中的每个质数的个数
bool st[N];
// 线性筛。找出 1~n 中的所有质数
void get_prime(int n){
    for (int i = 2; i <= n; i ++ ) {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ ) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}
// 高精度乘法的模板
vector<int> mul(vector<int> a, int b) {
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ ) {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t) {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}
// 计算出 n! 中质数 p 出现的次数
// 这里有个脑筋急转弯，除以 p^2 等于连续除以两个 p
int get(int n, int p) {
    int res = 0;
    while (n) {
        res += n / p;
        n /= p;
    }
    return res;
}
int main() {
    int a, b;
    cin >> a >> b;
    get_prime(a);  // 步骤一，分解质因数求出 1~a 的所有质因子
    // 步骤二，求出 C (a,b) 中每个质因子的个数。
    for (int i = 0; i < cnt; i ++ ) {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    // 步骤三，使用高精度乘法把所有的质因子乘起来。
    vector<int> res;
    res.push_back(1);
    for (int i = 0; i < cnt; i ++ ) {
        for (int j = 0; j < sum[i]; j ++ ) {
            res = mul(res, primes[i]);
        }
    }
    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");
    return 0;
}
# 实际应用
给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。
输出的答案对 109+7 取模。
# 举个例子
给出 3 个 0 和 3 个 1，满足条件的序列有以下 五 个：
  1. 000111；
  2. 001101；
  3. 001011；
  4. 010011；
  5. 010101；
# 题目分析
本题看上去比较无厘头，所以我们可以把题目转换一下，变成另一个问题：给出一个坐标系，问从一个点走到另一个点总共有多少种走法。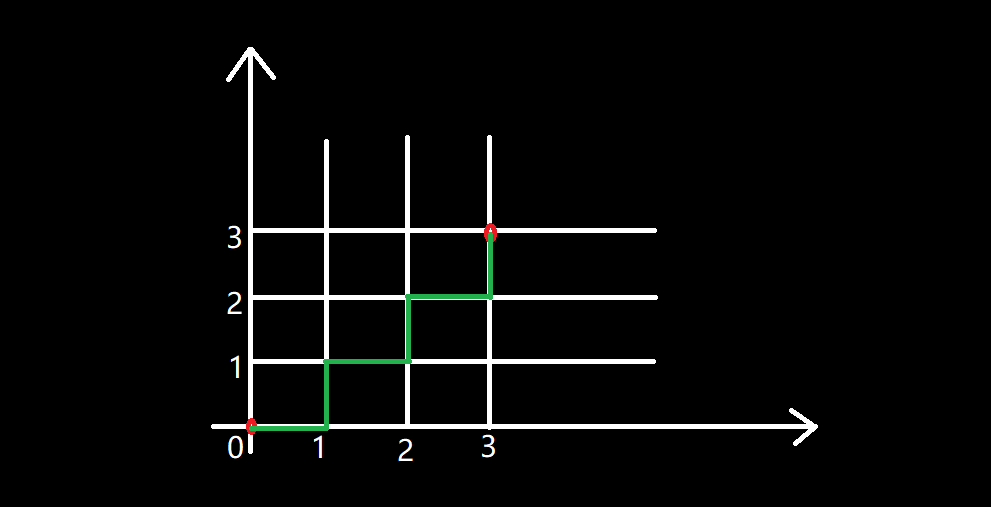
我们计算坐标从点 (0,0) 走到点 (3,3) 的方案，假设向右走一格表示 0，向上走一格表示 1，则图中绿色路径的方案可以表示为：010101，是一种合法方案。
用这种方式，我们把所有的合法方案都可以一一对应到一种路径上。那么，如何判断一个方案是否为合法方案呢？我们依旧可以通过坐标系表示出来。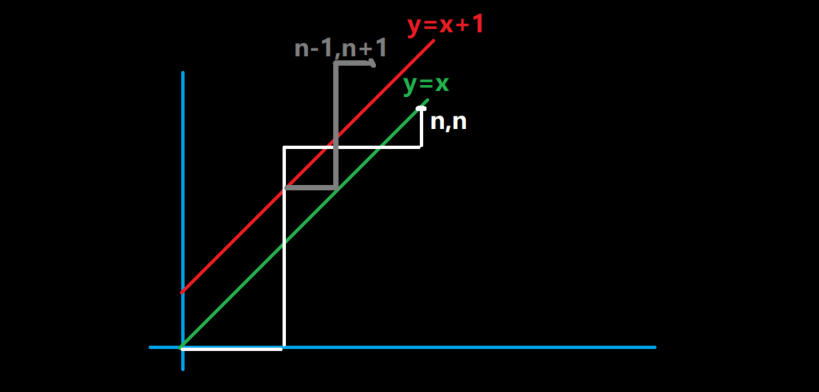
在绿线及以下表示合法，触碰红线表示不合法。其中白色线表示一条从 (0,0) 走到 (n,n) 的路径，因为触碰了红线，所以是不合法路径。
从图中可以看出，任何一条不合法路径（白色路径），必然对应一条从 (0,0) 走到 (n-1,n+1) 的路径（灰色路径）。这是因为灰色路径与白色路径是关于红线对称构造的。
进一步的，我们可以得到一个推论，即：任意不合法的路径都可以映射为一条到 (n-1,n+1) 的路径。（认真观察一下不难想到，这是因为点 (n-1,n+1) 与 (n,n) 是关于红线对称的。）
此时，我们就能想到所有的合法路径，其实就是用总的路径个数减去不合法的路径个数。
那么，总的合法路径个数怎么求呢？其实就是总共需要用 2n 步走到点 (n,n) ，那么向上走的步数就是 n 步，这不就是组合数嘛，从 2n 步中选出 n 步向上走，那么总方案数是C2nnC_{2n}^{n} 。
不合法方案数是什么呢？
所有的不合法方案一定是往右走 n-1 步，剩下的都往上走，所以不合法方案数都是从 2n 步中选出 n-1 步往右走的方案，也就是C2nn−1C_{2n}^{n-1} 。
合法的总方案数就是
C2nn−C2nn−1=(2n)!(n!)∗(2n−n)!−2n!((n−1)!)∗((2n−(n−1))!)=(2n)!(n!)∗(n)!−(2n)!∗n((n−1)!)∗((n+1)!)=(2n)!∗(n+1)n!∗(n+1)!−(2n)!∗(n+1)n!∗(n+1)!=(2n)!∗(n+1)−(2n)!∗n(n+1)!n!=(2n)!∗(n+1−n)(n+1)!n!=(2n)!(n+1)!n!=1n+1∗(2n)!n!∗n!=C2nnn+1\begin {array}{c} C_{2n}^{n}-C_{2n}^{n-1} & = & \frac {(2n)!}{(n!)*(2n-n)!}- \frac {2n!}{((n-1)!)*((2n-(n-1))!)} \\ & = & \frac {(2n)!}{(n!)*(n)!}- \frac {(2n)!*n}{((n-1)!)*((n+1)!)} \\ & = & \frac {(2n)!*(n+1)}{n!*(n+1)!}- \frac {(2n)!*(n+1)}{n!*(n+1)!} \\ & = & \frac {(2n)!*(n+1)-(2n)!*n}{(n+1)!n!} \\ & = & \frac {(2n)!*(n+1-n)}{(n+1)!n!} \\ & = & \frac {(2n)!}{(n+1)!n!}= \frac {1}{n+1}*\frac {(2n)!}{n!*n!} \\ & = & \frac {C_{2n}^{n}}{n+1} \end {array}
该公式有一个通用的名字，叫做卡特兰数，并且是很多组合数求解方案的通用解法。
# Code
输入样例：
3
输出样例：
5
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int mod = 1e9 + 7 ;
// 快速幂板子，用来求逆元
int qmi(int a, int k, int p) {
    int res = 1;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}
int main() {
    int n;
    cin >> n;
    int a = 2 * n, b = n;
    int res = 1;
    // 2n 的阶乘
    for (int i = a; i > a - b; i -- ) res = (LL)res * i % mod;
    // 快速幂求逆元  b 的阶乘的逆元
    for (int i = 1; i <= b; i ++ ) res = (LL)res * qmi(i, mod - 2, mod) % mod;
    // 在乘上 n-1 的逆元
    res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;
    cout << res << endl;
    return 0;
}
END
 
 更新于   阅读次数  次
请我喝[茶]~(￣▽￣)~*
A Cat Without Sugar 微信支付
微信支付
A Cat Without Sugar 支付宝
支付宝