manacher 算法是非常巧妙的算法，它与 KMP 的思想一样，都是利用已知的条件避免重复工作。该算法只有一个作用就是求解最长回文串的问题。

# 问题描述

给定一个长度为 n 的由小写字母构成的字符串，求它的最长回文子串的长度是多少。

示例：

输入：a b c b a b c b a b c b a

输出：13

回文串的含义是无论从前往后读，还是从后往前读，这个字符串都是一样的。

# manacher 算法

在 O (n) 的时间复杂度下求出给定字符串中的最长回文子串。

# 步骤一：转换

回文串可能有两种形式，偶数串和奇数串，在奇数串中一定有一个字符将左右两边分隔，从而形成对称的左右串。

但是在偶数串中没有这样一个字符，因此转换的目的就是把原字符串，转换为奇数串。此时转换后的奇数串中的回文串一定能在原字符串中找到与之对应的。

转换的方式就是用不在字符串中出现的字符 (下面用的是 "#")，将每个字符串中字符都分开，并用两个特殊字符放在首尾表示开始和结束。

为什么这样做一定能保证原串是奇数串呢？注意对比加工前后的字符串长度。任何整数先乘 2 都会变成偶数，再加一，一定会变成奇数。

原串：初始字符串。

新串：加工后字符串

加工后长度 = 初始串长度 * 2 + 1

原串与新串中的回文串对应关系如下：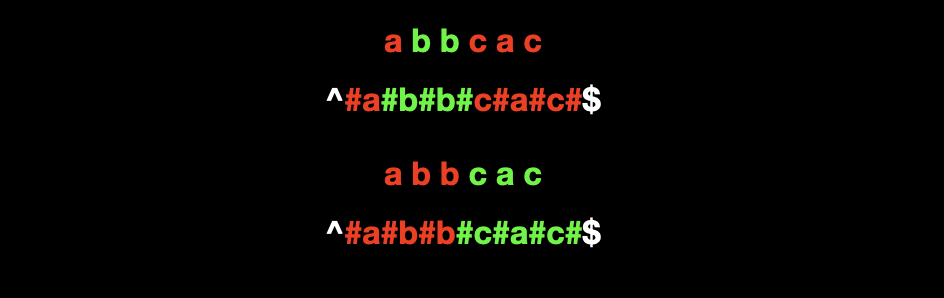

从图中的对应关系中可以看出，在原串中偶数个数的回文串 "bb"，在新串中的对应串也是奇数。

回文串的半径：以奇数串中心字符为准，向两侧可以延伸的最大长度（包括中心字符）。回文串 "#b#b#" 的半径是 3。回文串 "#c#a#c#" 的半径是 4。

根据回文串半径的定义，我们可以发现一条重要性质，原回文串的长度等于新串中与其对应的回文串的半径减一。（比如原串中的回文串 "bb" 的长度等于新串中与其对应的回文串 "#b#b#" 的半径 3，再减一，也就是 2。）

在拥有了这条重要性质之后，我们知道了原回文串的长度可以通过新回文串的半径得到，那么我们枚举新串中每个字符的回文串半径就可以找到最大的半径从而得到原串中的最大回文串。

p [i]：表示以字符 s [i] 为中心的最大回文串的半径（包含字符 s [i] 本身）。

# 步骤二：从左向右扫描

在维护时候，我们要维护一个当前右边界最靠右的回文串，假设当前的最靠右回文串的右边界为 mr (max_right)，中点为 mid。

靠右串：枚举到目前为止右边界最靠右的回文串。

mr：当前靠右串的右边界点。

mid：当前靠右串的中点。

枚举的当前点 i 会有两种情况：

1. 当前点 i 在回文串中，也就是 mid 右边，mr 左边（注意点 i 不可能在 mid 左面，因为枚举到点 i 的时候，mid 已经被枚举过了）。此时可能会存在两种情况。

第一种情况，以点 i 的对称点 j 为中心的回文串在靠右串内部。这种情况如下图所示。

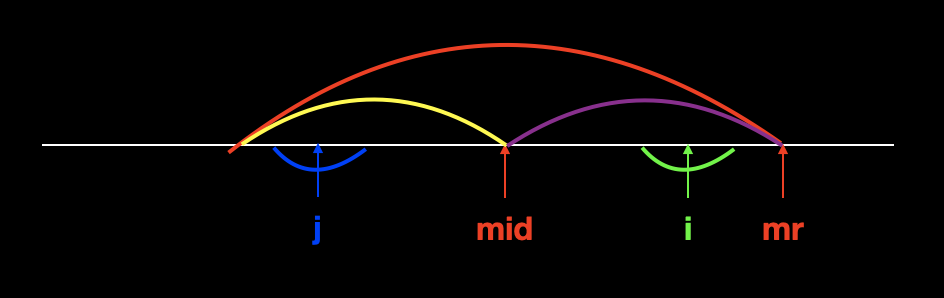
红色表示整个靠右串；

黄色紫色表示左右两边对称；

绿色表示当前点 i ；

蓝色表示的是点 i 的对称点 j ；

因为黄色紫色是对称的，所以有点 j 和点 i 是对称的。又因为以点 j 为中心的蓝色回文串都在靠右串的内部，所以以点 i 为中心的绿色回文串也一定在靠右串内部正好与其对称，也就有了 p [i] = p [j] 。

第二种情况，以点 i 的对称点 j 为中心的回文串延伸到靠右串外部。这种情况如下图所示。

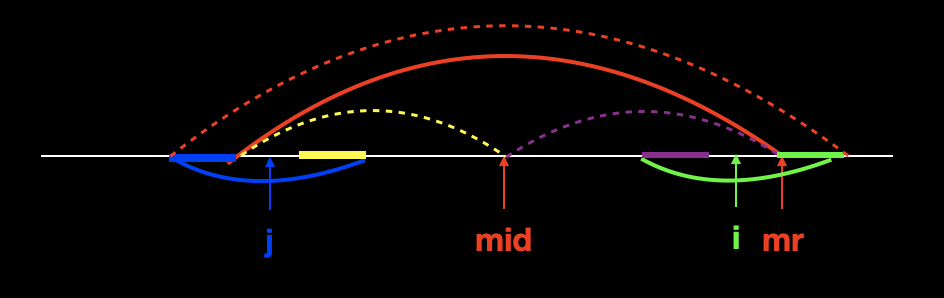
可以看到在这种情况中，以 j 为中心的蓝色回文串的左边一部分延伸到了靠右串的外部，因此作为 j 的对称串 i ，也有一部分延伸到了外部。

此时，因为绿色串以 i 为中心对称，所以加粗紫色部分与加粗绿色部分对称；因为虚线黄色与虚线紫色对称，所以加粗紫色部分与加粗黄色部分对称；因为蓝色串以 j 为中心对称，所以加粗蓝色部分与加粗黄色部分对称；最终我们推出结论，加粗绿色部分与加粗蓝色部分是对称的。

而通过最终结论和靠右串的定义，我们发现以 mid 为中心的靠右串竟然是虚线红色，这与事实不符（前面我们定义实线红色表示靠右串）。

所以，我们可以根据最终结论确认，以点 i 为中心的回文串右边界最大只能到 mr，此时就有了 p [i] = mr - i 。

综合一下上面的两种情况，我们可以发现，** 当点 i 处于靠右串内部，我们可以利用对称性，找到已知的对称点 j ，当 p [j] 完全在靠右串内部时候，p [i] 直接等于 p [j]；当 p [j] 延伸到靠右串外部，p [i] 就无法延伸到外部，因此只能是 mr - i ； 当 p [j] 踩在靠右串左边界的时候，p [i] 可以向外延伸。** 所以有以下结论：

p[i] >= min(p[j], mr - i)

2. 当前点 i 在靠右串外部。

此时无法利用已知条件的对称性，因此只能从 1 开始扩展，也就是 p [i] >= 1。

# Code

通过步骤二的分析，我们发现可以利用对称性，确定 p [i] 的下界，然后扩展点 i 两边的元素，如果相同就继续扩展，直到扩展到不相同为止，这样就求出了最终的 p [i]。

def manacher(s):

    s = '^#'+'#'.join(s)+'#$'

    # 每个字符自己都是回文串 初始化长度为 1.

    p = [1]*(len(s)-1)

    # 初始化 mid mr

    mid, mr = 1, 1

    # 循环时候无视掉首尾的占位字符

    # 因为我们设定首尾占位符不同 后面的 while 循环到首尾会自动停止

    for i in range(2, len(s)-1):

        # i 在靠右串内部

        if i < mr - 1:

            # mid = (i + j) / 2 推出 j = mid * 2 - i

            p[i] = min(p[mid * 2 - i], mr - i)

        # p [i] 是半径；i - p [i] 是左边；i + p [i] 是右边

        while s[i - p[i]] == s[i + p[i]]:

            p[i] += 1

        # 以 i 为中心的回文串的右边界超过了当前的右边界 则更新 mid mr

        if i + p[i] > mr:

            mid, mr = i, i + p[i]

    return max(p) - 1

print(manacher(input()))

# 时间复杂度分析

整体时间复杂度为 O (n)。主要是因为 while 循环最多只能执行一次，我们分几种情况进行讨论。

1、当 p [j] 完全在靠右串内部时候，p [i] 直接等于 p [j]，因此无法扩散，while 只能循环一次；

2、当 p [j] 延伸到靠右串外部时候，p [i] 只能取到 mr - i ，此时 while 依旧只能循环一次；

3、当 p [j] 正好踩在靠右串左边界的时候，p [i] 也正好取到靠右串的右边界，此时我们不知道右边界的下一个字符是否构成回文，因此进行扩展，而每次扩展右边界都会被增大，这个右边界最大会被扩展到 n。

综上所述，while 循环最多执行 n 次，整体复杂度是 O (n) 的。