# LeetCode 373. 查找和最小的 K 对数字

给定两个以 升序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。

定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。

请找到和最小的 k 个数对 (u1,v1),  (u2,v2)  ...  (uk,vk) 。

示例 1:

输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释：返回序列中的前 3 对数：[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
示例 2:

输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释：返回序列中的前 2 对数：[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]

示例 3:

输入: nums1 = [1,2], nums2 = [3], k = 3
输出: [1,3],[2,3]
解释：也可能序列中所有的数对都被返回:[1,3],[2,3]

提示:
1 <= nums1.length, nums2.length <= 105
-109 <= nums1[i], nums2[i] <= 109
nums1 和 nums2 均为升序排列
1 <= k <= 1000

# 题目分析

先来简单看一下题意：
给出两个整数数组，两个数组的所有数字两两组合，变成一个新的数组，返回新的数组中 和最小 的 k 个元素。

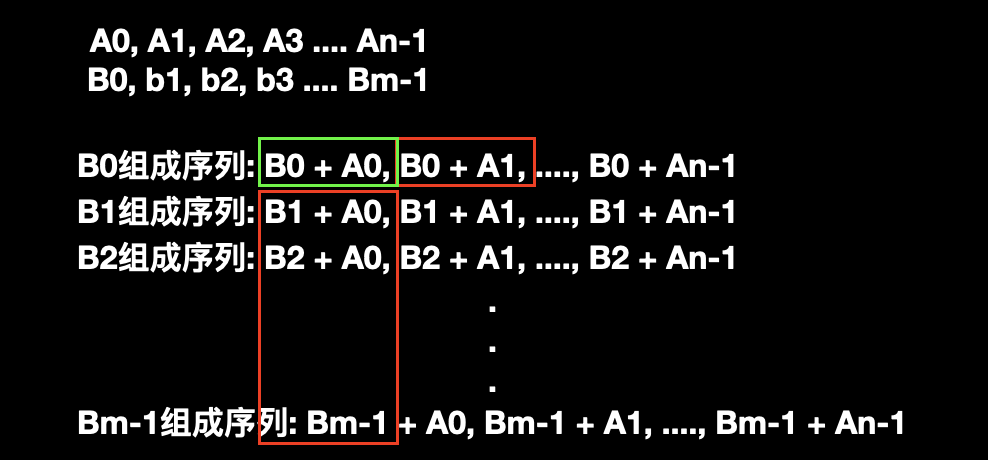
两两组合后，会产生如下图所示序列：

从图中可以直观的看到共组成了 m 个新序列，而每个新序列中 B 是不变的而 A 在递增，所以每个新序列也是递增的。

而我们的最终目标是在这 m 个新递增序列中，找出前 k 个最小元素，也就是一个多路归并的过程。

# 多路归并

初始化时候，把每个序列中的最小值放到堆里，这样每次取出来的元素 cur 就是最小的，取出来之后，把 cur 所在序列的下一个元素放到堆里。

1. 每个序列中最小的全部入堆。
   

2. 取出堆顶的最小元素，并把该元素所在序列的下一个元素入堆。
   
   其中绿色为最终结果，红色为堆中元素。

3. 重复做步骤 1 和 2，直到满足要求。

# Code

import heapq

def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:

    if not nums1 or not nums2:

        return []

    n, m = len(nums1), len(nums2)

    # 初始化堆 先把每个序列的第一个元素入堆。

    # 新序列的 B 是 0~m-1，加入首个 A，下标均是 0

    heap = []

    for i in range(m):

        # heap 中元素格式：("B+A", A 下标，B 下标)

        heapq.heappush(heap, (nums2[i] + nums1[0], 0, i))

    res = []

    while k and heap:

        cur = heapq.heappop(heap)

        # 结果格式：[A, B]

        res.append([nums1[cur[1]], nums2[cur[2]]])

        # 把剩余的 A 也算上。

        if cur[1] + 1 < n:

            # 入堆当前元素所在序列的下一个元素。

            # 也就是当前元素所在序列 A 下标加 1，B 不变。

            heapq.heappush(heap, (nums1[cur[1] + 1] + nums2[cur[2]], cur[1] + 1, cur[2]))

        k -= 1

    return res