# 前缀和的作用

解决的问题：给定一个数组 nums 和 m 次询问，两个整数 left 和 right，表示一个询问的区间范围。

# 暴力解法

从题面上分析这种问题暴力做法想要求出来基本上要遍历 nums 中到 right 的数，然后一个个相加到 left，在一个个相加到 right。在暴力的算法中可以看到我们两次计算了 nums [0....left] 的部分，并且询问次数 M+1，就需要多遍历两次。

# 前缀和优化

前缀和的思路其实就是预处理 nums 中每个数得出来他们与前面所有元素相加之和为新的元素，这些新的元素就成了前缀和数组。利用该数组轻松的就能在 O (1) 的时间复杂度下解决上述问题。

nums = [0] + nums

sums = [0] * (len(nums) + 1)

for i in range(1, len(nums)):

    # 在这里 sums [i - 1] 就是当前元素的前面所有元素之和

    # nums [i] 就是当前元素值，把它们加起来放到前缀和数组。

    sums[i] = nums[i] + sums[i - 1]

可以看到其中的下标都是从 1 开始的，这是因为如果不从 1 开始在求区间和时候就要用到 sums[right] - sums[left - 1] ， left 在等于 0 的时候这个规则就不适用了，所以让下标都从 1 开始，给定数组前补一个元素 0 即可。这样我们求最终答案的代码就变成了： return sums[right + 1] - sums[left]

# 二维前缀和

给定一个二维矩阵 nums 和 m 次询问，四个整数 row1，col1，row2，col2，表示一个询问的区间范围，求这个范围内的子矩阵和。（为了方便直接就放今天的题好了，LeetCode 第 303 题）

二维的前缀和比一维要难处理不少的。

（借用一个图，哈哈哈，画的确实好。）

sums[O][D] = sums[O][C] + sums[O][B] - sums[O][A] + D
其实求翻译一下就是想求前缀和 [O][D]， 就用 OC + OB，然后减去加了两次的 OA， 最后再加上 D 即可。

# 这里用 f 表示前缀和数组，matrix 表示二维矩阵

# row1， col1 表示左上角，row2， col2 表示右下角

f = [[0] * (m + 1) for _ in range(n + 1)]

f[0][0] = matrix[0][0]

for i in range(len(matrix)):

    for j in range(len(matrix[0])):

        f[i + 1][j + 1] = f[i][j + 1] + f[i + 1][j] + matrix[i][j] - f[i][j]

此处数组下标从 1 开始原因与一维相同，防止下面计算子矩阵时候下标越界。然后如何求答案呢？

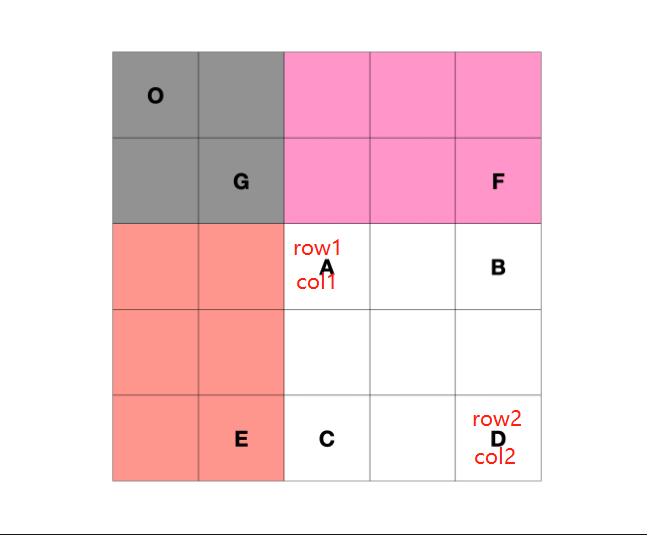
如果我们求 sums[A][D] ，那伪代码如下：

sums[A][D] = sums[O][D] - sums[O][E] - sums[O][F] + sums[O][G]
然后代码实现的时候，需要注意一下下标从 1 开始，所以用到 row2 和 col2 都要加一。代码实现如下：

return f[row2 + 1][col2 + 1] - f[row1][col2 + 1] - f[row2 + 1][col1] + f[row1][col1]
关键点：虽然二维前缀和看起来确实复杂不少，但是用心体会这个小技巧是有很强的技巧性的，在实现的时候要注意的是下标直接从 1 开始。在二维矩阵中把 row 当作横坐标，col 当作纵坐标。那么 E 这个点就是（row1， col2），F 这个点就是（row2， col1）。这样这道题其实变成了六年级图形题～～