# 前置知识
线段树 (上),线段树 (下),字典树
# 可持久化的数据结构
“可持久化” 指数据结构可以缓存其历史任意时刻的状态(参考 git 可以记录代码任意时刻是什么样的,并且也可以回滚到历史任意时刻)。
换言之,可持久化数据结构高效的记录该数据结构所有的里是状态。
要注意的是,并非 所有的数据结构都是 可持久化的。只有在操作的时候 数据结构整体 不会发生变化 才可以做持久化操作,比如,平衡树需要通过节点的左旋右旋维持平衡,所以在操作的时候平衡树的整体结构发生了变化,则不可以持久化!
考虑一下,使用暴力的方式应该怎么做呢?很简单,只要我们将所有的历史状态存储在数组中就可以做到,比如用 history [i] 记录某个数据结构操作 i 次之后的状态。但是,这样会使整体的空间和时间大幅增加。
而可持久化的核心思想是只会记录当前版本与前一个版本不一样的地方,如此整体的空间和时间会降低很多。
后面我们以字典树和线段树为例,具体看一下这种技巧如何使用。
# 可持久化字典树
字典树是一种高效的 存储 和 查找 字符串集合 的基础数据结构,又叫 Trie 树、前缀树等。
对于基础的字典树还不了解的小伙伴,可以先看这篇字典树。
# 字典树持久化后的结构
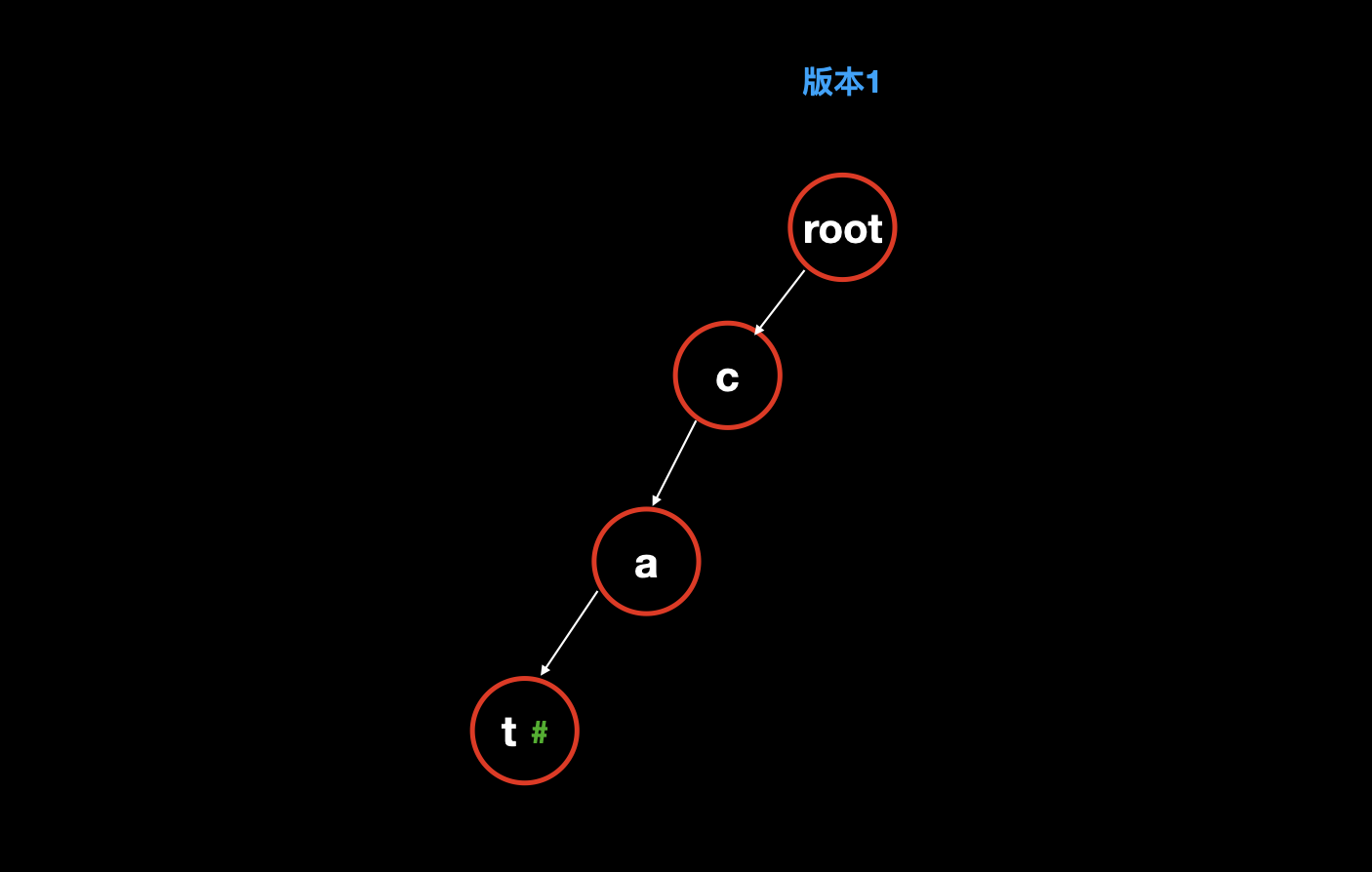
考虑我们需要存储到字典树的单词序列为: [cat, rat, cab, fry] 。我们先将基础的字典树结构创建出来。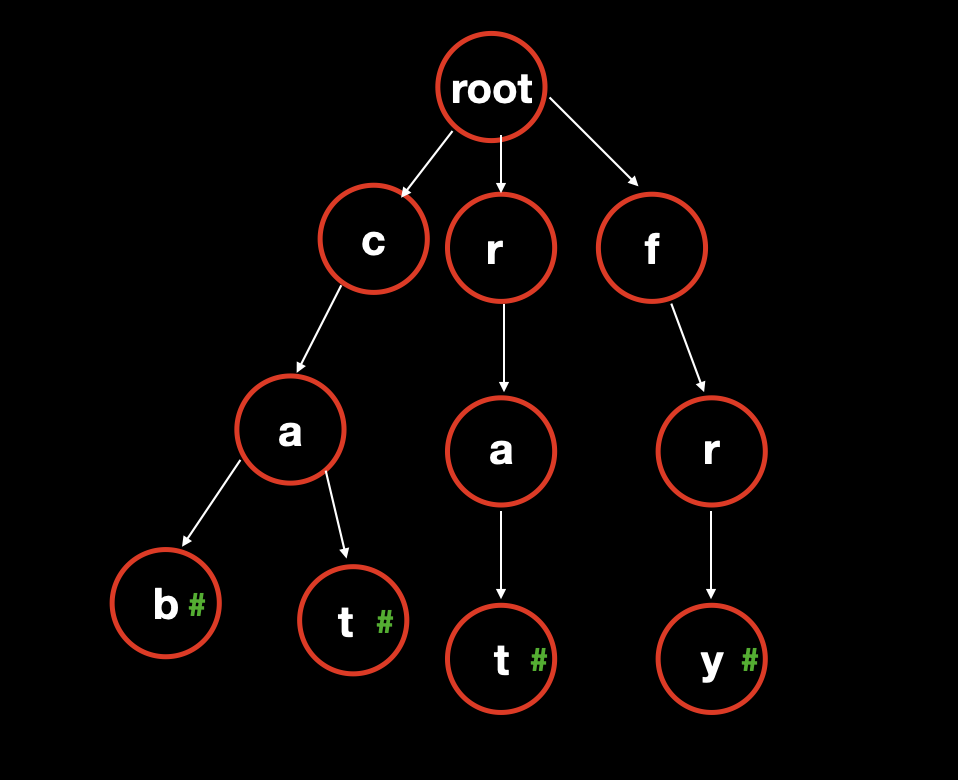
我们观察这个单词序列,总共有四个单词,也就是说我们会有四个插入操作,如此,我们就需要保存四个版本的字典树。
谨记我们的持久化规则,只新增 增量数据。
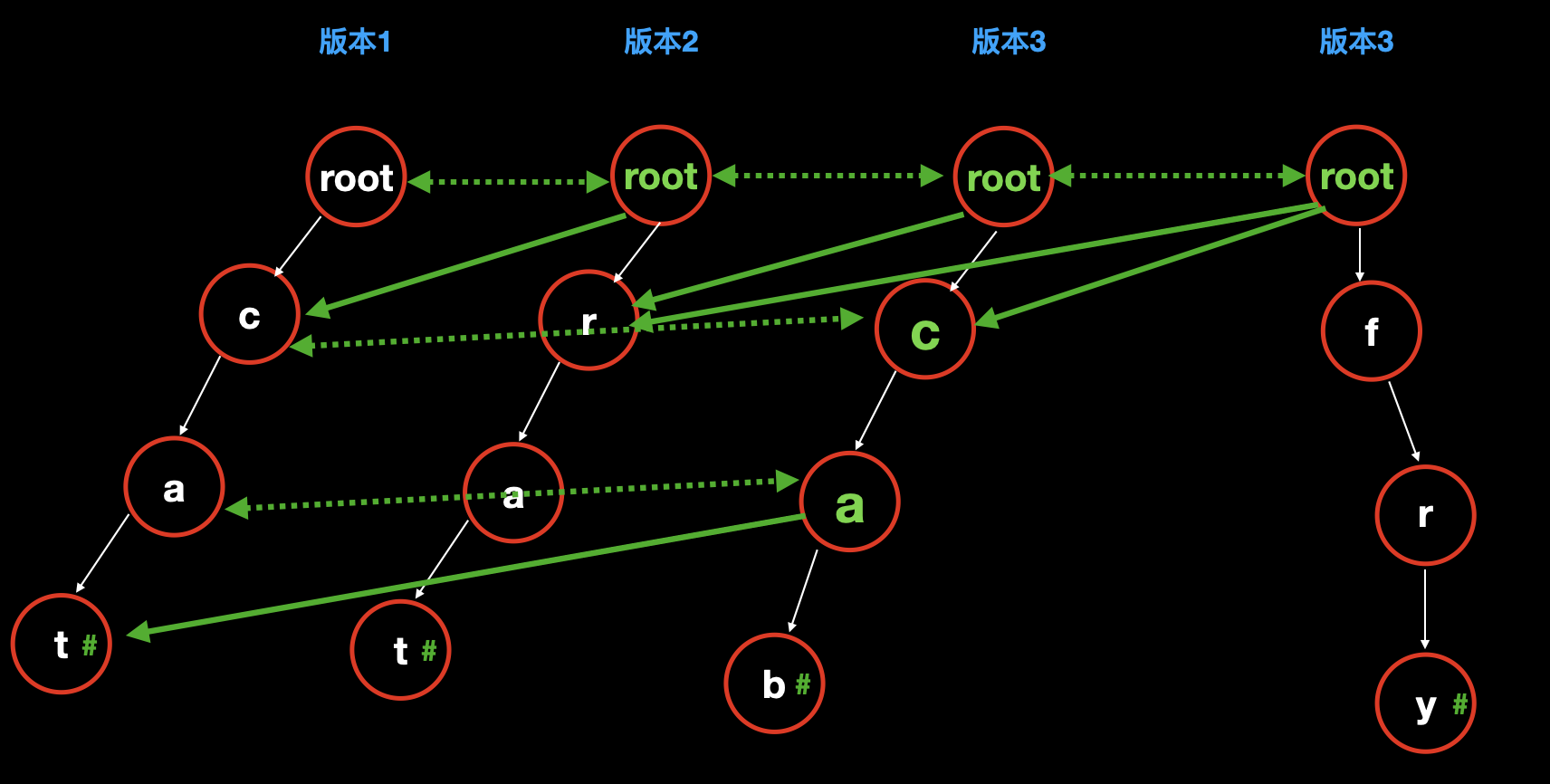
上图中所有颜色的含义如下:
- 白色节点和白色虚线:本次完全新增的节点;
- 绿色节点:本次新增的节点,但是这个新增是从双向绿色虚线指向的节点复制过来的。
- 绿色单向实线:表示直接指向以前的节点。
明确,图中颜色的含义后,则不难理解如上图所示的持久化字典树的建立过程:
完全新建以
cat为路径的字典树;![]()
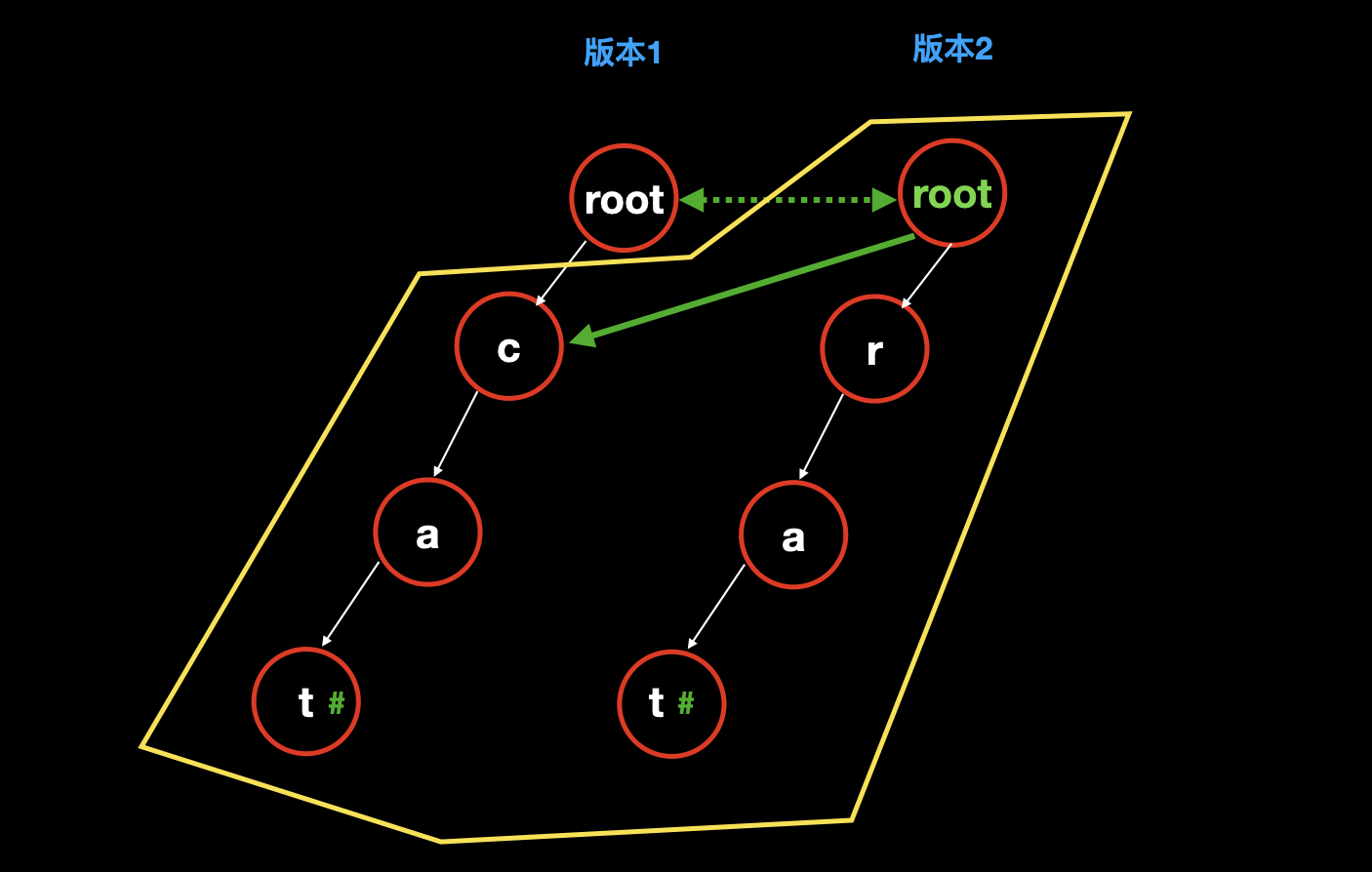
因为要新增单词
rat,需要注意的关键点是版本二中虽然也有分支 cat,但是用的却是版本 1 中的,所以不需要占用额外空间和时间:所以我们先把版本 1 的 root 复制一下,作为版本 2 的 root。
然后发现第一个字母
r是完全新增的字母,而以前的路径cat是完全不变的,所以我们直接把 root 指向版本 1 的cat。然后在 root 下新增
rat,此时版本 2 完成。![]()
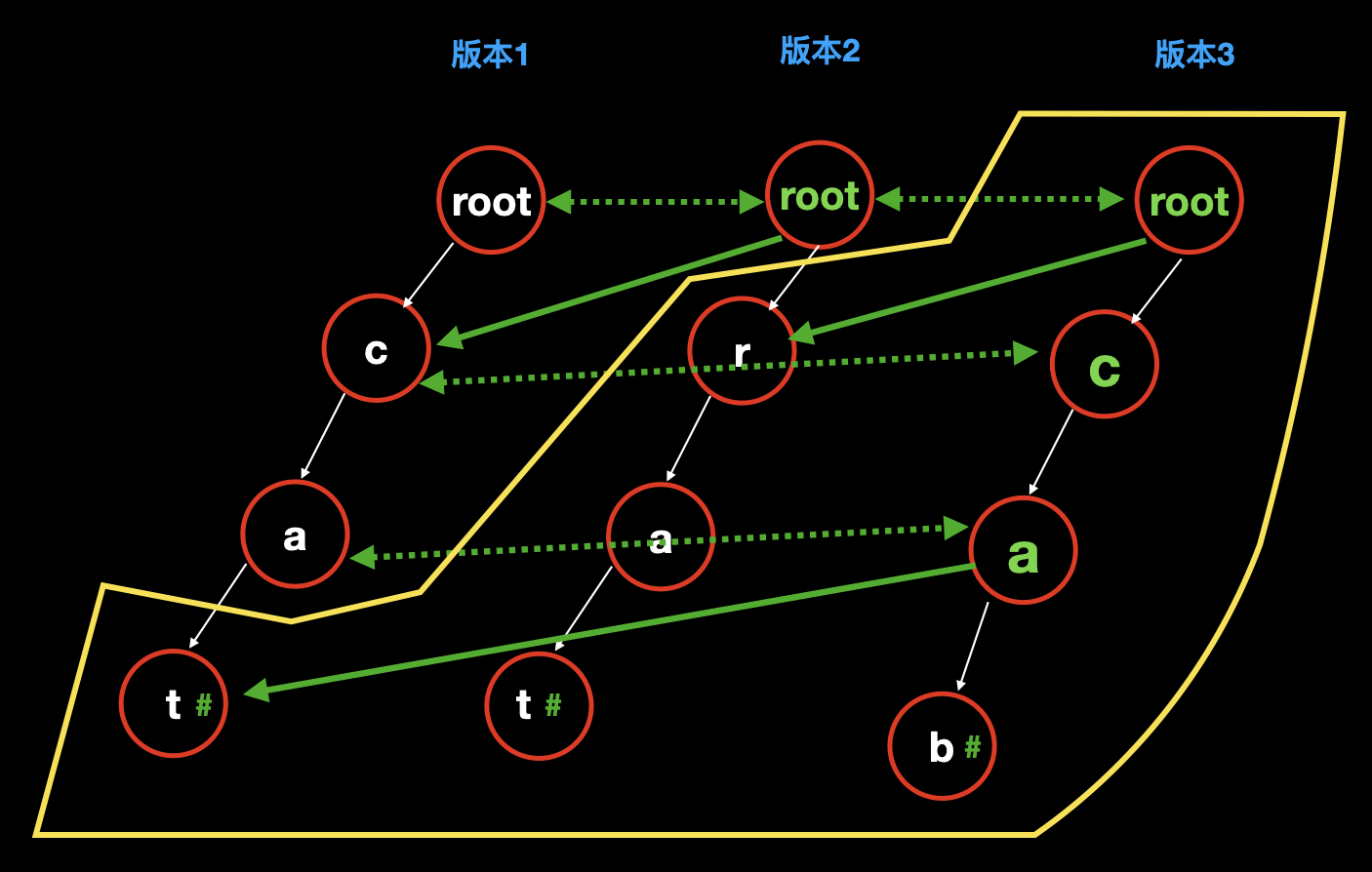
新增单词
cab:把版本 2 的 root 复制一下,作为版本 3 的 root。
发现字母
c和a虽然是新增的,但是在版本 2 中已经有了这两个节点,因此直接复制过来,放到 root 下。至此,在第一个路径
cat上还有一个字母 t 是非新增的,因此,我们直接让a指向t;把完全新增的 b 接到 a 后面;
![]()
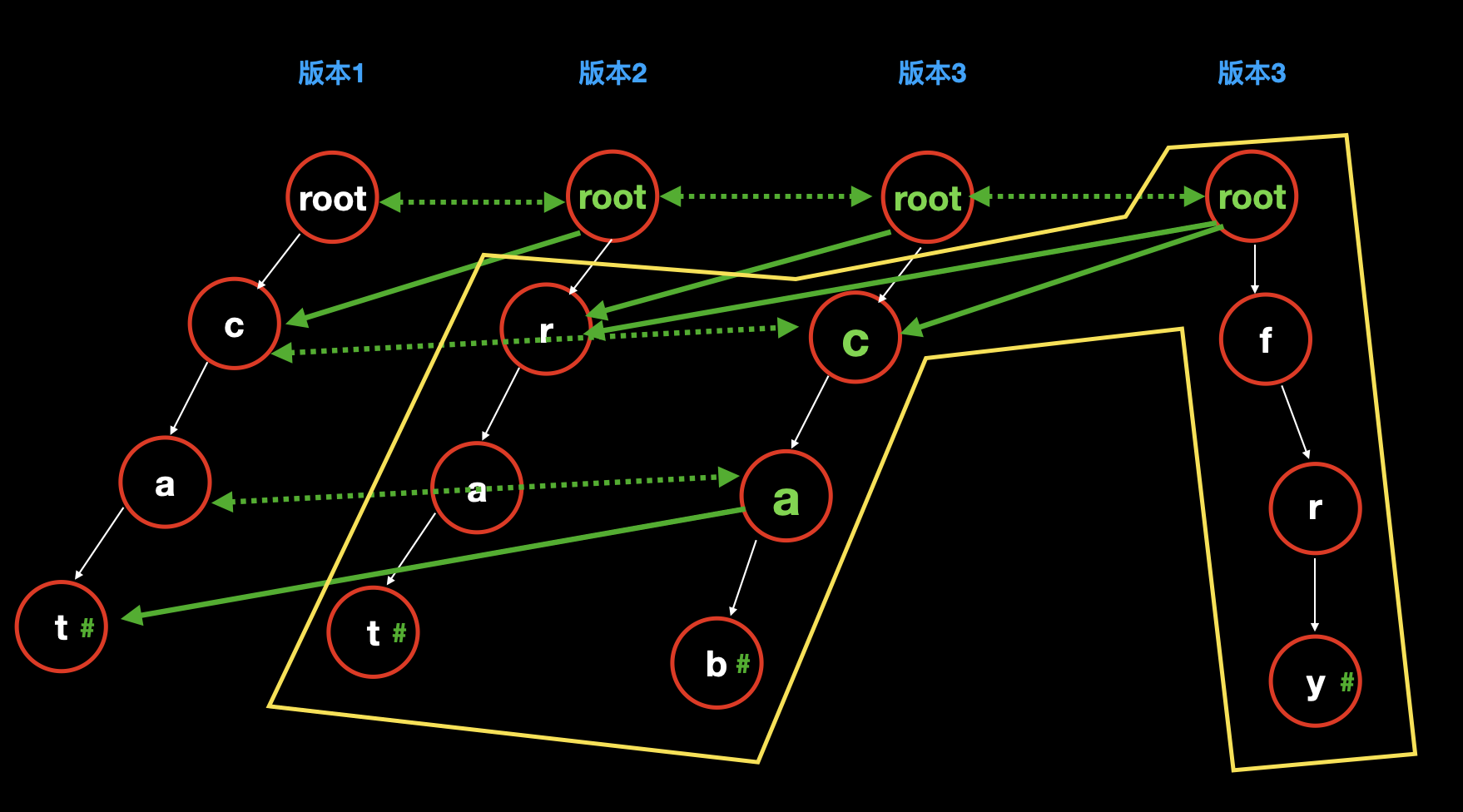
新增单词
fry:把版本 3 的 root 复制一下,作为版本 4 的 root。
我们发现 fry 是完全新增的,和上一个版本中的数据没有任何关系,因此,我们把它在 root 上新建出来;
然后让 root 指向上一个版本的其他数据,即可表示第四个版本。
![]()
# 伪代码
我们尝试一下用伪代码来描述一下上面的过程。
// 增加一个版本 | |
//root [i] 表示版本号 i | |
pre = root[i - 1]; // 首先 pre 指向上一个版本的 root | |
curr = root[i] = ++ idx; // 创建一个新的当前版本 curr | |
// 如果 pre 是空的 说明没有上一个版本 该版本就是最新版 | |
// 如果 pre 不是空的 我们先把 pre 整体克隆一下 | |
if (pre) tree[curr] = tree[pre]; | |
// 完全新增的儿子节点 si 放到 curr 里面; | |
tree[curr][si] = ++ idx; | |
// 更新 pre 和 curr 对比下一个节点是需要复制的 还是需要新增的 | |
pre = tree[pre][si], curr = tree[curr][si]; | |
// 接下来只需要循环该操作,完成本次插入的单词 |
# AcWing 256. 最大异或和
给定一个非负整数序列 a,初始长度为 N。
有 M 个操作,有以下两种操作类型:
- A x:添加操作,表示在序列末尾添加一个数 x,序列的长度 N 增大 1。
- Q l r x:询问操作,你需要找到一个位置 p,满足 l≤p≤r,使得:a [p] xor a [p+1] xor … xor a [N] xor x 最大,输出这个最大值。
输入格式
第一行包含两个整数 N,M,含义如问题描述所示。
第二行包含 N 个非负整数,表示初始的序列 A。
接下来 M 行,每行描述一个操作,格式如题面所述。
输出格式
每个询问操作输出一个整数,表示询问的答案。
每个答案占一行。
数据范围
N,M≤3×10^5, 0≤a[i]≤10^7。输入样例
5 5 2 6 4 3 6 A 1 Q 3 5 4 A 4 Q 5 7 0 Q 3 6 6输出样例
4 5 6
# 题目描述
本题是 AcWing 143. 最大异或对的加强版,我们在上篇攻略中,已经详细描述了 143 题的做法。
本题概念是这样的。给出一个非负的整数序列 A [],有两个操作:
- 添加操作。添加一个数到序列末尾;
- 查询操作。给出一个区间 [l,r] 和一个数 x,从该区间中找到一个数,该数一直到末尾的所有数以及 x 异或起来 结果最大。
我们来看下示例:
给出序列为 [2,6,4,3,6] ,经过第一个操作后变成 [2,6,4,3,6,1] ,接着遇到第二个操作,给出区间是 [3,5],给出的 x 是 4,结果如下图所示: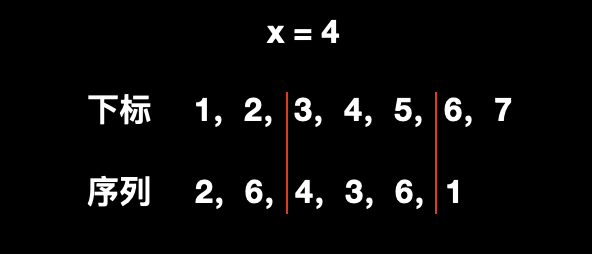
我们可以选择的数有 [4,3,6]:
选择 4,则用 4 和 它到序列末尾的所有数 [3,6,1] 以及 x 做异或运算,结果是
4^3^6^1^4=4;选择 3,则用 3 和 它到序列末尾的所有数 [6,1] 以及 x 做异或运算,结果是
3^6^1^4=0;选择 6,则用 6 和 它到序列末尾的所有数 [1] 以及 x 做异或运算,结果是
6^1^4=3;结果最大是 4。
# 题目分析
对于区间的操作,直接操作区间不是很方便,需要遍历区间的所有元素,那么是否可以使用简单的方式 求出某区间的 异或结果呢?
考虑以前学过的前缀和思想,我们可以预处理出来前缀异或的数组 S。
s[0] = 0;
s[1] = A[1];
s[2] = A[1] ^ A[2];
.
.
.
s[i] = A[1] ^ A[2] ^ ... ^ A[i];
这样做的好处是,当我们在 给定区间内选出一个数 p 的时候,求 A[p]^...^A[n]^x ,就相当于是求 s[p-1]^s[n]^x 。
我们发现后面的部分 s[n]^x 是一个固定的值,假设它是 c ,那么我们的目标就变成了在区间 [L,R] 中选择出来一个数 p,使得 s[p-1]^c 最大。
回忆一下 143 题中,我们的做法,在 143 题中我们要求整个序列的异或最大值,我们把整个单词序列都存储到了 01 字典树中。
而在本题中,需要找到 [L,R] ,这个区间的最大值 p。我们可以迂回考虑,假如是求区间 [1,R] 中的最大值 p,该怎么做呢?
这里我们就可以使用到持久化字典树了,因为字典树 root[r] 版本中存储了 [1,R] 中的所有数据。
那么对于左端点 L 的限制,应该如何处理呢?只需要保证,前缀异或 路径上的节点 的历史版本 大于 L 就可以了,也即是保证了选择的数在给定区间内。
所以,对于持久化字典树的每一个节点 维护一个额外信息 max_id 表示它属于哪个历史版本。
考虑每个节点 i 的 max_id 如何更新呢?
从建树的过程中我们知道一个节点 i 的子节点,要么连接在之前的版本 的节点 i 上,要么是 在创建了 新的节点 1 之后,再 创建出来它的子节点,所以,我们其实只要知道 节点 i 的子节点 的最大版本号,就是 节点 i 所属的 max_id。
# Code
#include <iostream> | |
#include <cstdio> | |
#include <algorithm> | |
#include <cstring> | |
using namespace std; | |
// 这里 M 的大小为什么乘以 25 呢? 因为我们要把 给定序列 a [] 中的整数变成 | |
// 二进制 而 a [i] 的极限值是 10^7 换算成二进制需要 2^24 算上根节点 root 就是 25 | |
// 所以字典树的树高度最多是 25 | |
const int N = 600010, M = N * 25; | |
int n, m; | |
int max_id[M]; | |
int tree[M][2], root[N], idx; | |
int s[N]; | |
//i 表示前缀异或数组 的 下标 也就是当前存储的数字 s [i] | |
//k 表示当前处理到了二进制的第几位 | |
//pre 表示 数据 s [i] 的第 k 位 上一个版本中的情况 (是否存在?) | |
//curr 表示当前版本 | |
void insert(int i, int k, int pre, int curr) { | |
// 整个数字插入完毕 记录它是第 i 个被插入的数 | |
if (k < 0) { | |
max_id[curr] = i; | |
return ; | |
} | |
//s [i] 为插入数字 取出第 k 位 | |
int v = s[i] >> k & 1; | |
// 数据 s [i] 的第 k 位 存在于上一个版本中的 | |
// 则把上一个版本中的 其他位 复制过来 | |
if (pre) tree[curr][v ^ 1] = tree[pre][v ^ 1]; | |
// 把当前位 创建出来 | |
tree[curr][v] = ++ idx; | |
// 递归创建 下一个二进制位 即 k-1 | |
insert(i, k - 1, tree[pre][v], tree[curr][v]); | |
// 因为当前位 max_id 的更新 需要子节点的数据 | |
// 所以当递归到底的时候 要自底向上的更新当前的 max_id | |
max_id[curr] = max(max_id[tree[curr][0]], max_id[tree[curr][1]]); | |
} | |
//root 表示某个版本的根节点 也就是 右端点 | |
//c 表示当前用来查询的值 也就是 s [n] ^ x 的结果 | |
//l 表示左端点的限制 | |
int query(int root, int c, int l) { | |
// 查询 就和 标准的字典树查询非常的相似了 | |
int pre = root; | |
// 需要注意的是 这里 直接用 23 个二进制位 来构建 [l,r] 中的一个数就行 | |
for (int i = 23; i >= 0; i -- ) { | |
int v = c >> i & 1; //c 的第 i 位 | |
// 那么要找的就是 v^1 如果有符合条件的 根节点下的 v^1 就选择 | |
// 注意我们的 max_id 默认为 - 1 如此肯定不会 >=l | |
// 如果 max_id 默认为 0 则 l 也是 0 就会跳到不存在的节点 | |
if (max_id[tree[pre][v ^ 1]] >= l) pre = tree[pre][v ^ 1]; | |
// 否则 只能使用 v 了 | |
else pre = tree[pre][v]; | |
} | |
//max_id [pre] 就是我们最终找到的 s [] 中的下标 与上 c 就是最终结果 | |
return c ^ s[max_id[pre]]; | |
} | |
int main() { | |
cin >> n >> m; | |
max_id[0] = -1; // 初始化根节点的 max_id | |
root[0] = ++ idx; | |
// 首先插入一下 根节点也就是 s [0] (注意 s [0] 的值是 0) | |
insert(0, 23, 0, root[0]); | |
// 读取整个序列 并以 持久化的方式 插入到字典树 | |
for (int i = 1; i <= n; i ++ ) { | |
int x; | |
scanf("%d", &x); | |
s[i] = s[i - 1] ^ x; // 求 异或前缀数组 | |
// 每插入一个数字 都是一个新的版本 | |
root[i] = ++ idx; | |
insert(i, 23, root[i - 1], root[i]); | |
} | |
char op[2]; | |
int l, r, x; | |
while (m -- ) { | |
scanf("%s", op); | |
if (*op == 'A') { | |
// 插入一个数字到末尾 | |
scanf("%d", &x); | |
n ++ ; | |
s[n] = s[n - 1] ^ x; | |
root[n] = ++ idx; | |
insert(n, 23, root[n - 1], root[n]); | |
} else { | |
scanf("%d%d%d", &l, &r, &x); | |
// 查询中要注意的是 我们想查的是在原数组 [l,r] 中找到 p | |
// 但是 我们使用了 前缀异或数组 它的第一位 s [0]=0 在原数组中不存在 | |
// 也就是说 是有一位下标偏移的 | |
// 所以在原数组中找 [l,r] 前缀异或数组 中对应的是 [l-1, r-1] | |
printf("%d\n", query(root[r - 1], s[n] ^ x, l - 1)); | |
} | |
} | |
return 0; | |
} |
# AcWing 255. 第 K 小数
给定长度为 N 的整数序列 A,下标为 1∼N。
现在要执行 M 次操作,其中第 i 次操作为给出三个整数 li,ri,ki,求 A [li],A [li+1],…,A [ri] (即 A 的下标区间 [li,ri]) 中第 ki 小的数是多少。
输入格式
第一行包含两个整数 N 和 M。
第二行包含 N 个整数,表示整数序列 A。
接下来 M 行,每行包含三个整数 li,ri,ki,用以描述第 i 次操作。
输出格式
对于每次操作输出一个结果,表示在该次操作中,第 k 小的数的数值。
每个结果占一行。
数据范围
N≤10^5,M≤10^4,|A[i]|≤10^9输入样例
7 3 1 5 2 6 3 7 4 2 5 3 4 4 1 1 7 3输出样例
5 6 3
# 题目描述
给一个数组 A [1~n],执行 M 次操作,每次操作给出一个区间 [L,R] 和一个正数 k ,求出区间 [L,R] 中第 k 小的数。
# 题目分析
本题是非常经典的题目,做法非常多,但是今天要学习的是可持久化的数据结构,所以我们使用持久化的线段树来解决本题。
本题需要以数值区间(而不是下标)建立线段树,然后维护每个区间中 数的数量 cnt。
考虑如何找到第 k 小的数呢?
假设,先不考虑左右区间 [L,R] 的限制,我们就在 [0,n-1] 的整体区间上找到第 k 小的数。
这样可以使用二分法。如何二分呢?注意我们线段树区间节点中存储的是区间内有多少个数,那么很明显的二段性是:第 k 小的数 必然 在整体区间 的前 k 个数里面,因为题目中说明给出的序列 A 是整数序列。
所以我们把整体区间进行二分:
- 如果
[0,mid]的cnt满足cnt>=k,说明在区间 [0,mid] 中已经有至少 k 个数,那么第 k 小的数也必然在其中,所以我们就可以递归左边; - 反之,递归右边。
那么如果把区间 [L,R] 的限制也考虑进来该怎么做呢?
我们可以先看 [1,R] 的这个区间,此时 root[R] 就是只有前 R 个数的版本的信息,假设 cntR 为 [1,R] 这个区间的信息。
再来看左端点的限制,在第 root[L-1] 个版本中,假设 cntL 保存了节点 [1,L-1] 的信息,那么我们想要知道 [L,R] 的信息,就可以用 cntR-cntL 。
所以,我们在做递归的时候,需要同时递归 R 和 L-1 两个版本,这样就可以计算出 [L,R] 之间的 cnt ,也就可以用上面二分的方法来找第 k 小的数。
# Code
本题给出的序列最多只有 10^5 个数,但是数的范围却是 [-10^9 ~ 10^9] ,所以需要离散化一下。
#include <cstring> | |
#include <algorithm> | |
#include <iostream> | |
#include <vector> | |
using namespace std; | |
const int N = 100010, M = 10010; | |
int a[N]; | |
vector<int> nums; | |
int n, m; | |
// 节点数量 除了原来的 N*4 之外 | |
// 还要算上持久化用到的 N * logN | |
struct Node { | |
int l, r; | |
int cnt; | |
}tree[N * 4 + N * 17]; | |
int root[N], idx; | |
int find(int x) { | |
return lower_bound(nums.begin(), nums.end(), x) - nums.begin(); | |
} | |
// 初始化 线段树的整体结构 每个数字的插入使用 insert | |
int build(int l, int r) { | |
int curr = ++ idx; | |
if (l == r) return curr; | |
int mid = l + r >> 1; | |
tree[curr].l = build(l, mid), tree[curr].r = build(mid + 1, r); | |
return curr; | |
} | |
//pre 表示上一个根节点 | |
//l 和 r 表示增加的左右端点 | |
//x 表示的是要增加的数 离散化后的位置 | |
int insert(int pre, int l, int r, int x) { | |
// 插入的过程类似 持久化字典树 | |
// 增加一个新的当前版本 | |
int curr = ++ idx; | |
// 先复制上一个版本到当前版本 | |
tree[curr] = tree[pre]; | |
// 区间长度为 1 的时候 就是 x 的位置 把 x 放在这里 当前版本 curr 的 cnt++ | |
// 要注意的是 线段树只是保存区间里面的元素个数 | |
// 所以插入其实就是找到对应的位置然后 cnt 增加 | |
if (l == r) { | |
tree[curr].cnt ++ ; | |
return curr; | |
} | |
int mid = l + r >> 1; | |
// 插入的数 小于 mid 则插入到左面 否则插入到右面 | |
// 递归插入的时候 也要注意这里的细节 是递归插入到了子节点 而非 pre | |
if (x <= mid) tree[curr].l = insert(tree[pre].l, l, mid, x); | |
else tree[curr].r = insert(tree[pre].r, mid + 1, r, x); | |
// 这里的细节一定要注意 我在这写错了 debug 了很久很久。。。 | |
// 这块其实就相当于 线段树中的 pushup 操作了 子节点计算根节点 | |
// 而 curr 的两个子节点 其实是 tree [curr].l 和 tree [curr].r | |
tree[curr].cnt = tree[tree[curr].l].cnt + tree[tree[curr].r].cnt; | |
return curr; | |
} | |
// 其中 R 表示 [1, R] 版本 root [R] 包含的所有数 | |
// L 表示 左边界的 L 我们需要剔除 [1,L-1] | |
//l 和 r 分别表示当前查询的左右边界 k 即题目给出的 k | |
int query(int R, int L, int l, int r, int k) { | |
// 我们一直保证 [l,r] 中包含答案,那么如果只有一个数 那么这个数就是答案 | |
if (l == r) return r; | |
//tree [tree [R].l].cnt 表示存在于 R 的左子树里面数的个数 | |
//tree [tree [L].l].cnt 表示存在于 L 的左子树里面数的个数 | |
// 两者相减 表示 存在于 R 的左子树 但是不包含在 [1, L] 中的数的个数 | |
int cnt = tree[tree[R].l].cnt - tree[tree[L].l].cnt; | |
int mid = l + r >> 1; | |
// 如果 k 在 cnt 之内 递归到左面 也就是 [tree [L].l, tree [R].l ] | |
if (k <= cnt) return query(tree[R].l, tree[L].l, l, mid, k); | |
// 否则 递归到右边 注意递归到右边之后 所求的 k 在右边是 k-cnt | |
else return query(tree[R].r, tree[L].r, mid + 1, r, k - cnt); | |
} | |
int main() { | |
cin >> n >> m; | |
for (int i = 1; i <= n; i ++ ) { | |
scanf("%d", &a[i]); | |
nums.push_back(a[i]); // 离散化 先放到 nums | |
} | |
// 离散化 | |
sort(nums.begin(), nums.end()); | |
nums.erase(unique(nums.begin(), nums.end()), nums.end()); | |
root[0] = build(0, nums.size() - 1); // 初始化一下节点 0 | |
// 插入一个数就算一个版本 | |
for (int i = 1; i <= n; i ++ ) | |
root[i] = insert(root[i - 1], 0, nums.size() - 1, find(a[i])); | |
while (m -- ) { | |
int l, r, k; | |
scanf("%d%d%d", &l, &r, &k); | |
printf("%d\n", nums[query(root[r], root[l - 1], 0, nums.size() - 1, k)]); | |
} | |
return 0; | |
} |
END