# 前置知识

本文第一部分（算法介绍部分）与这篇文章完全相同。但用作示例的题目不同，本文的题目更贴合实际应用，而这篇文章的题目更加的偏向模板，而且用 python 写的。

二分图的概念在图论基础之染色法判定二分图。本文主要讲述判定二分图的算法匈牙利算法。

二分图的匹配：给定一个二分图 G，在 G 的一个子图 M 中，M 的边集 {E} 中的任意两条边都不依附于同一个顶点，则称 M 是一个匹配。

二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

# 匈牙利算法

# 抽象模型

该算法的主要作用就是求二分图的最大匹配的数量。

该算法可以用 “比喻” 来理解。

我们把自己看做 “月老”，二分图的一部分是 “男同学集合”，另一部分是 “女同学集合”。两个集合中的某些同学具有好感，我们的目的是 “把具有好感的男女同学匹配为情侣，要求是匹配的情侣数量最多”。

如下图，互相连线表示具有好感，我们要在其中找出可以匹配的最大数量。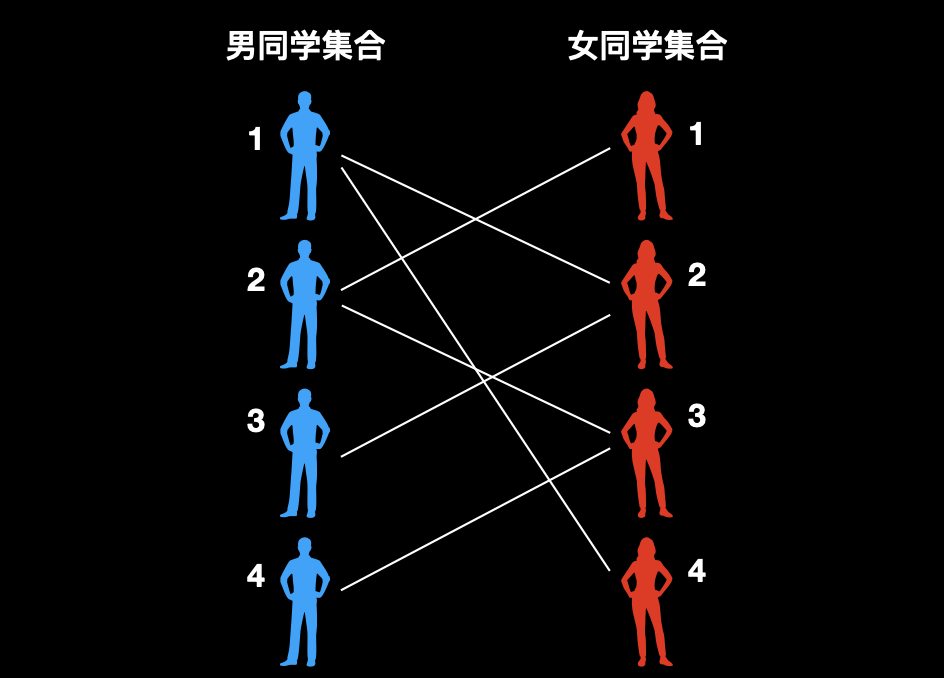

# 算法流程

遍历整个男同学集合，从第一个男同学开始，寻找和他具有好感的女同学，只要找到了就暂时把他俩配成一对。

如果和当前男同学 X 具有好感的女同学 A 已经被配对给了别的同学怎么办呢？此时比较常规的做法是继续去和下一个具有好感的女同学配对。

但是，该算法的做法是找到和这位女同学 A 匹配的男同学 B 是哪位，看下这位男同学 B 是否有其他的女同学 C 可以配对，如果有就让这位男同学 B 和其他人 C 配对。这样当前男同学 X 就可以和女同学 A 进行配对啦。

示例

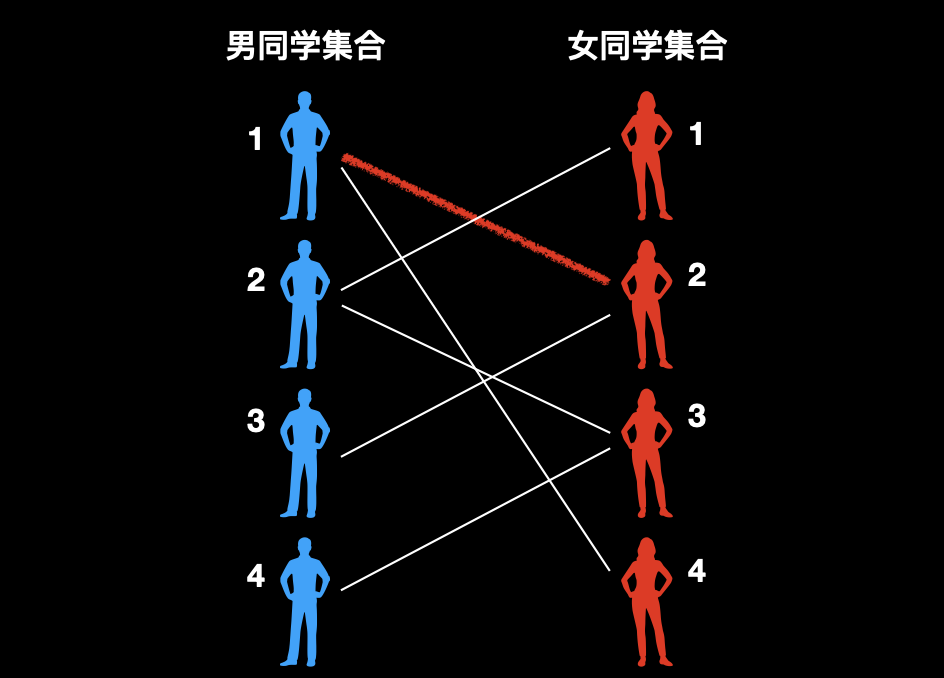
遍历到 1 号男同学，发现他和 2 号女同学具有好感，因此，我们先将他俩连一条红绳。
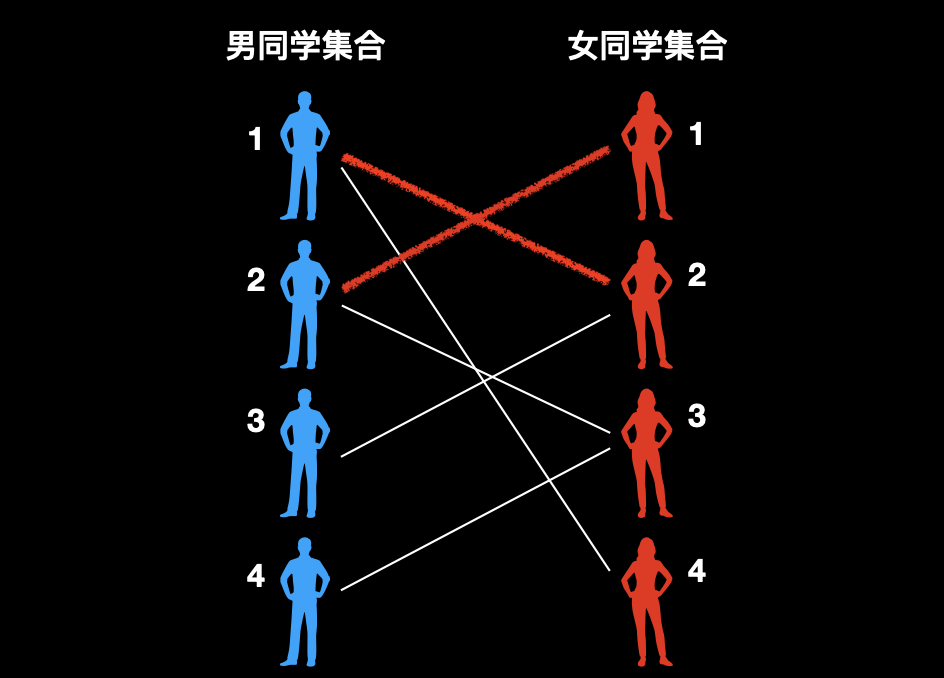
遍历到 2 号男同学，发现他和 1 号女同学具有好感，因此，他俩也可以连一条红绳。
遍历到 3 号男同学，发现他和 2 号女同学具有好感，2 号女同学已经和 1 号男同学配对了。
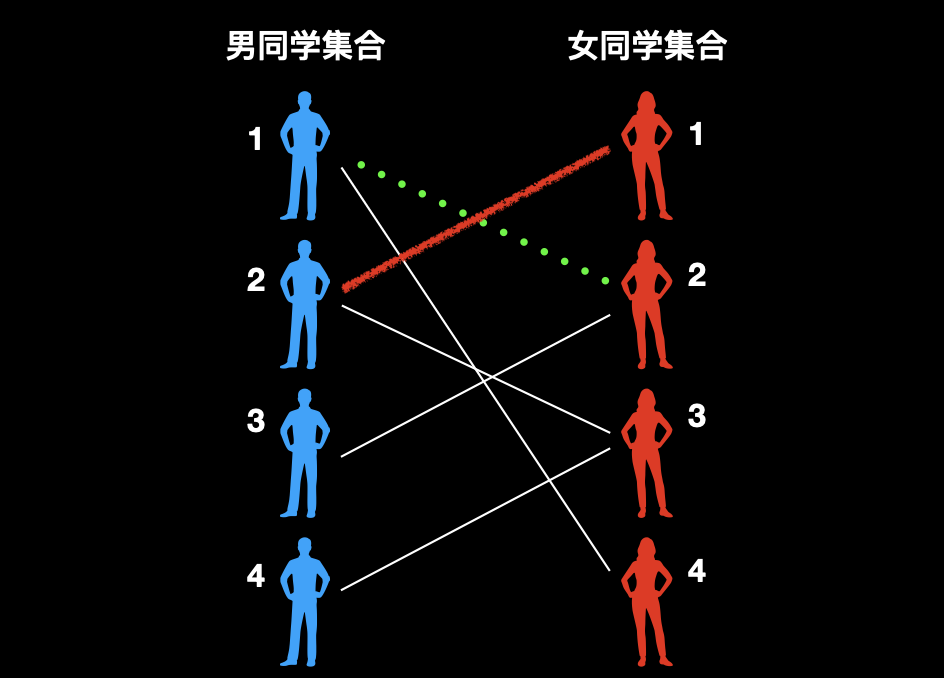
此时关键来了，再看 1 号男同学发现他还和 4 号女同学具有好感，那么问题就简单了。我们给 1 号男和 2 号女一条绿绳子，让他们分开。
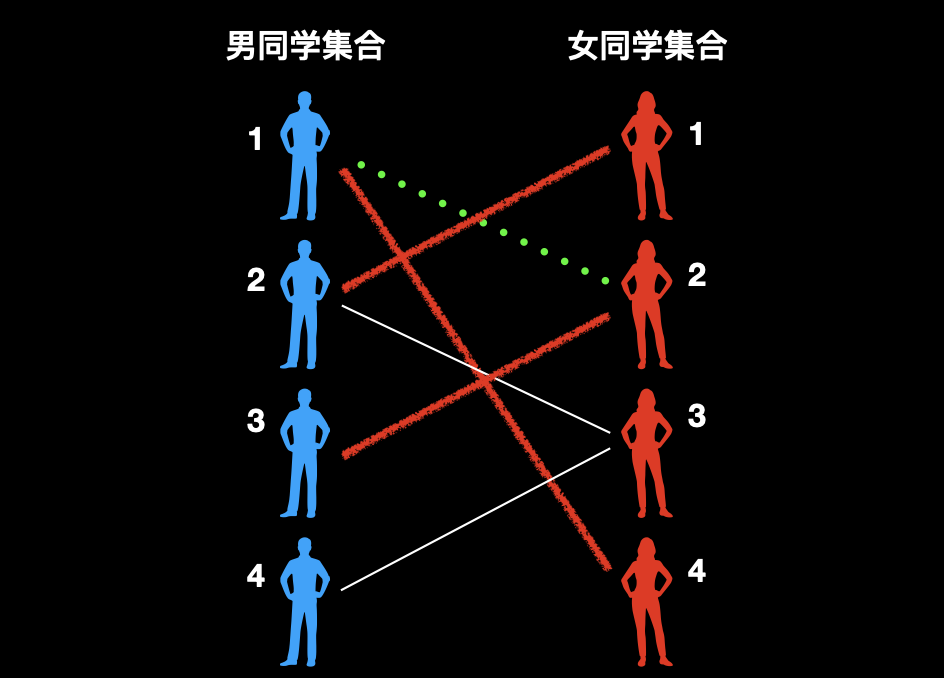
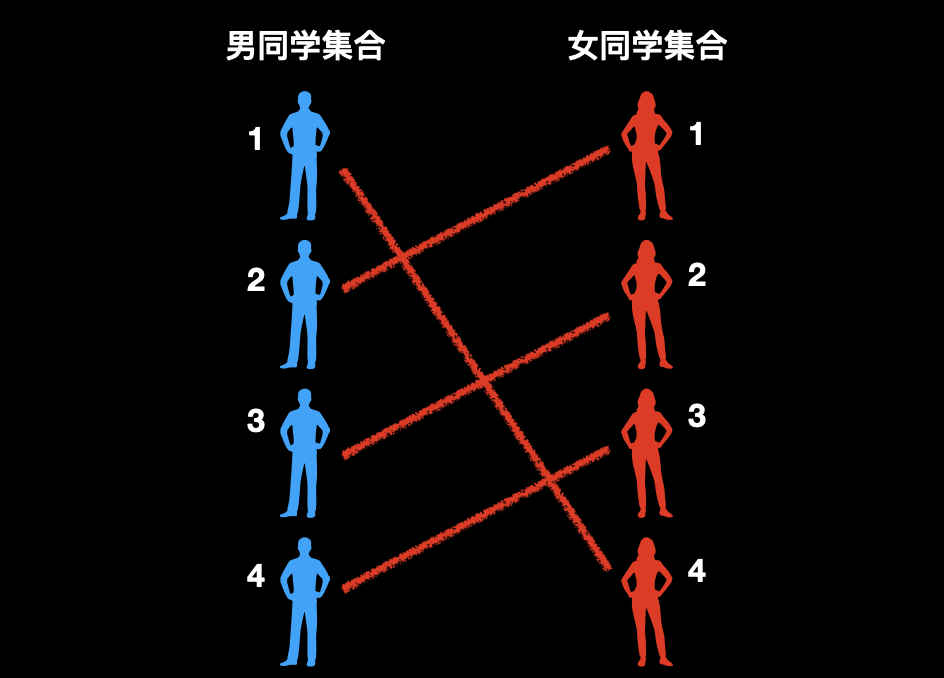
然后再把 1 号男和 4 号女配对，3 号男和 2 号女配对，皆大欢喜。
最后把 4 号男和 3 号女配对。获得最大匹配数量，4 对。

# AcWing 372. 棋盘覆盖

给定一个 N 行 N 列的棋盘，已知某些格子禁止放置。
求最多能往棋盘上放多少块的长度为 2、宽度为 1 的骨牌，骨牌的边界与格线重合（骨牌占用两个格子），并且任意两张骨牌都不重叠。
输入格式
第一行包含两个整数 N 和 t，其中 t 为禁止放置的格子的数量。
接下来 t 行每行包含两个整数 x 和 y，表示位于第 x 行第 y 列的格子禁止放置，行列数从 1 开始。
输出格式
输出一个整数，表示结果。
数据范围
1≤N≤100,
0≤t≤100
输入样例
8 0
输出样例
32

# 题目描述

一个 n*n 的棋盘，想在上面放长 2 宽 1 的骨牌，并且有些格子不可以放，问最多可以放多少块骨牌。

# 题目分析

乍一看，和二分图好像没有啥关系，但是我们可以调整一下思路，我们发现本题的骨牌所占面积是长度 2 宽度 1，也就是无论竖着放还是横着放都要占用两个单位的格子，无形之中似乎和二分图产生了玄之又玄的联系。

进一步的，我们把每个格子都抽象为点，那么两个格子放置一块骨牌，就可以被看作是两个相邻点之间连了一条边，继续按照这个模型思考，我们发现所有连的边是不能有公共点的，因为每个格子只能被使用一次，不可能两条边使用了同一个格子。如此，我们发现本题转换成了最多选取多少条边，可以使选中的边没有公共点，这就是我们上面最大匹配的含义。

那么，如何才能和二分图扯上关系呢？

在染色法判定二分图中，我们知道了二分图一定可以被染成两种颜色，使得每条边的两个点一定是不同颜色的。

基于上述性质，有一种经典的做法，我们可以把所有的格子分为奇数格和偶数格，作为二分图的两个集合，分别染不同的颜色，染色之后，我们就可以发现整个图可以被成功染色。

上图中，我们假设整个棋盘根据奇数格和偶数格被染成黑蓝两种颜色，最终结果我们发现任意横或者竖占两个单位面积的骨牌均是由黑蓝两色组成的。

因此，整个问题就可以抽象为以格子作为点，相邻两点之间可以连接一条边，问最多可以选取多少条边，使选中的边没有公共点，并且整个图符合二分图。

# Code

在实现中，需要考虑一个小问题，如何判断奇数格或者偶数格呢？

我们可以直接把每个格子的横坐标和纵坐标加起来的和，作为一个点，如果点是奇数，就是奇数格；点是偶数，就是偶数格。

	#include <iostream>
	#include <cstring>

	#define x first
	#define y second

	using namespace std;

	typedef pair<int, int> PII;

	const int N = 110;
	int n, m;
	bool g[N][N], st[N][N];
	PII match[N][N];
	int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};

	// 匈牙利算法模板
	int find(int x, int y) {
	// 遍历当前点的四个邻点
	for (int i = 0; i < 4; i ++ ) {
	int a = x + dx[i], b = y + dy[i];
	if (a < 1 or a > n or b < 1 or b > n) continue;
	// 判断点是否合法以及是否已经被使用了
	if (g[a][b] or st[a][b]) continue;
	st[a][b] = true; // 标记邻点已经使用
	PII t = match[a][b]; // 邻点的配对情况
	// 未配对或者能给邻点的配对换掉
	if (t.x == 0 or find(t.x, t.y)) {
	// 就把当前点和邻点配对
	match[a][b] = {x, y};
	return true;
	}
	}
	return false;
	}

	int main() {
	cin >> n >> m;
	while (m -- ) {
	int a, b;
	cin >> a >> b;
	g[a][b] = true;
	}
	int res = 0;
	for (int i = 1; i <= n; i ++ ) {
	for (int j = 1; j <= n; j ++ ) {
	// 匈牙利算法模板只遍历一个集合从所有的偶数点找
	if ((i + j) % 2 and !g[i][j]) {
	memset(st, 0, sizeof st);
	if (find(i, j)) res ++ ;
	}
	}
	}
	cout << res << endl;
	return 0;
	}

END

经典必会 AcWing算法提高课匈牙利算法二分图的最大匹配