首页 算法 数据结构

本文参考：https://www.acwing.com/video/264/

# 二叉堆

堆是个很大的概念，而本文中的堆，是由二叉树来实现的，所以其实本文的堆特指为二叉堆。

# 概念

优先队列：一种特殊的队列，顾名思义，它可以在 O (1) 的时间复杂度下 pop 出 max/min。

二叉堆：堆有多种的形式，但是我们一般而言的 heap 就是二叉堆，即由完全二叉树来实现的堆，比如：python 中的 heapq。

二叉堆是优先队列的一种实现形式。

# 堆的作用

一般而言，堆的主要作用有以下几点：

  1. 快速的 peek 出 max/min 元素，时间复杂度 O (1)。
  2. 快速的 pop 出 max/min 元素，时间复杂度 O (1)。
  3. 快速的插入一个数到堆中，时间复杂度 O (logn)。

# 堆的结构

二叉堆的结构其实就是一颗满足堆性质的完全二叉树，二叉树的每个节点均有权重，根据权重的不同，我们又可以分成大根堆和小根堆。

其中大根堆的重要性质是所有节点的权重均小于等于其父节点，也就是说大根堆的 root 节点一定是最大的。

反之，小根堆与大根堆正好相反，小根堆的所有节点的权重均大于等于其父节点，也就是说小根堆的 root 节点一定是最小的。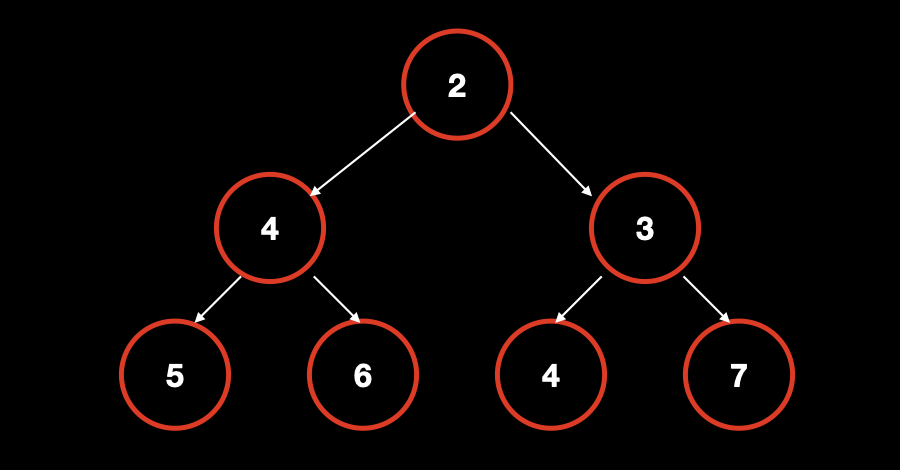

# 堆的存储

根据完全二叉树的性质，我们可以使用数组来存储整棵树。具体地：

  1. 把节点编号（是节点编号而非权重）作为数组中存储的下标；
  2. 左子节点编号为父节点编号乘 2；
  3. 右子节点编号为父节点编号乘 2 加 1；

使用这种方式，我们把小根堆中的元素标上编号，并且存储到数组中。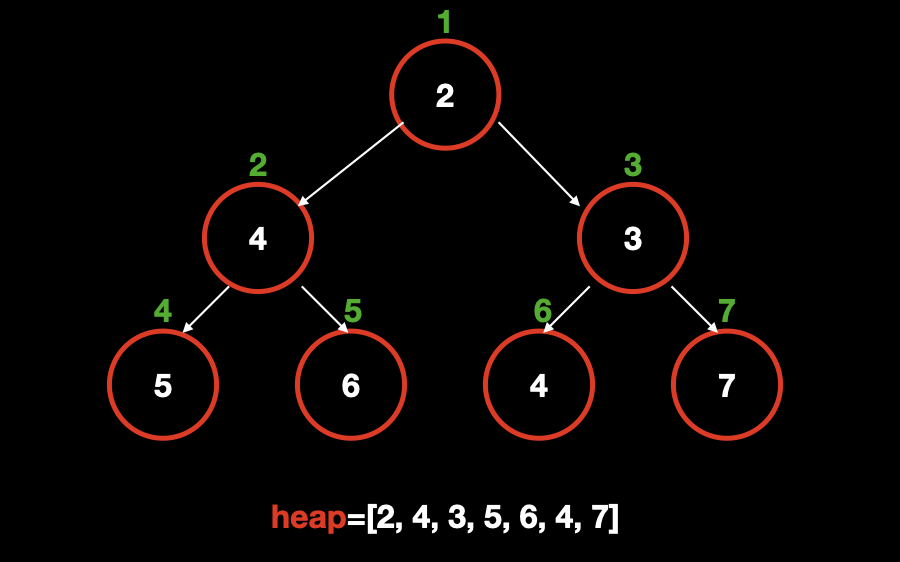

这种方式有什么好处呢？显而易见的是，节省空间，与普通的树结构存法（邻接表等）相比，不需要指针来判断父子节点关系，另一个好处是可以直接用 节点编号除以 2 来快速的获取父节点。

# 实现堆的两个主要操作

我们可以发现，无论大根堆还是小根堆，为了满足相关的性质都需要调整节点在堆中的位置，而调整节点在堆中的位置的操作，我们分为两种，一种是将节点下沉 (down)，一种是将节点上升 (up)，下面以小根堆为例：

  1. 参数说明：

    1. h 数组 存储堆中所有的元素，定义在全局；
    2. 节点 u 当前正在调整的节点，由方法的参数传入；
    3. idx 当前 h 数组中元素的最大下标（或者叫 数组中元素个数），定义在全局；

  2. down: 因为是小根堆，必须要保证所有节点的权重均大于等于其父节点，为了满足这一点，我们要比较当前节点和它的两个子节点，选出三个节点中最小的那个当做新的父节点，具体的做法是：

    1. 初始化 当前最小节点 t 为 当前节点 u ；
    2. 比较 当前最小节点 t 和 当前节点 u 的左子节点 u*2 的权重大小，如果左子节点比 u 更小，说明 u 需要下沉，更新 当前最小节点 t 为 u 的左子结点；
    3. 比较 当前最小节点 t 和 当前节点 u 得右子节点 u*2+1 的权重大小，如果右子节点比 t 更小，同样说明 u 需要下沉，更新 当前最小节点 t 为 u 的右子结点；
    4. 如果当前最小节点 t 和 当前节点 u 不相同，则说明当前节点 u 大于它的儿子节点，不符合小根堆性质，所以把当前节点 u 与 当前最小节点 t 交换（也就是把 非当前最小节点的 u 下沉，所以称为 down）；
    5. 递归 down (t)，以保证当前节点的调整不会影响整体上小根堆性质，最坏情况是从根节点 down 到叶子节点，也就是 down 操作的最坏时间复杂度为 O (logn)，其中 n 为树的高度。
void down(int u) {
    int t = u;  // 临时存储 最小节点 以便后续比较。
    //u * 2 为左子节点， 如果左子结点小于等于数组中的最大下标，说明左子节点存在；
    // 那么我们判断左子结点的值 h [u * 2] 是否小于 当前节点 h [t]，符合条件则记录 t 为左子节点。
    if (u * 2 <= idx && h[u * 2] < h[t]) t = u * 2;
    //u * 2 + 1 为右子节点，同理，右子节点也需要和 当前节点 h [t] 比较。
    if (u * 2 + 1 <= idx && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    // 如果 t 和 u 不相同，说明最小节点有过变更，则交换 u 和当前的最小节点。
    if (u != t) {
        swap(u, t);
        // 递归 down (t) 
        down(t);
    }
}
  1. up：与 down 操作正好相反，down 是把父节点下沉，而 up 操作是把一个节点上升，即，交换一个节点和它的父节点，以达到小根堆的性质。
    1. 判断 当前节点 u 是否存在 父节点 (u/2)，如果父节点 (u/2) 是大于 当前节点 u 的说明不符合小根堆性质，则把当前节点 u 与父节点交换（即，把更大的当前节点和其父节点互换，以满足小根堆，每个节点都小于等于它的子节点）。
    2. 循环 u /= 2，把当前的节点的父节点置为新的当前节点（当然也可以像 down 操作一样使用递归）。
void up(int u) {
    // 父节点 u / 2
    while (u / 2 && h[u / 2 ] > h[u]) {
        swap(h[u / 2], h[u]);
        u /= 2;  //u = u / 2 变成父节点
    }
}

# 实现堆的功能

如果能理解，上面的两种操作，我们就可以用这两种操作来实现一个二叉堆。

  1. peek 出 max/min，也就是选出最大或者最小元素，那么直接根据大根堆 / 小根堆的性质，堆顶（根节点）就是 max/min。
// 大根堆的根节点即是最大值，小根堆为最小值。
int get_top() {
    return h[1];
}

  1. pop 操作，也就是删除堆顶元素。在删除的时候，如果直接删除掉堆顶的元素，那么会出现一种情况：补充新的根节点，需要把两个子节点较小的那个上升；上升后，为了补充缺失子节点，又要判断子节点的两个子节点哪个需要上升，一直循环到叶子节点，这样无疑是很麻烦的。

    所以，我们可以使用一个小技巧来删除，即，使用最后的元素来覆盖根节点，删掉最后的元素，把根节点 down 一遍即可。总时间复杂度是 O (logn)。

void pop() {
    h[1] = h[idx -- ];
    down(1);
}
  1. insert 操作，也就是插入一个数到堆中，为了避免影响到堆中现有元素，我们同样使用一个小技巧来插入元素，即，先把元素放到最后，然后对其执行 up 操作即可。总时间复杂度同样是 O (logn)。
void insert(int val) {
    h[++ idx] = val;
    up(idx);
}

# 进阶功能

上面的三种功能，是堆的标准功能，也就是各个语言提供的标准堆支持的功能，而我们实现的堆，还可以提供进阶的功能：

  1. 删除任意一个元素 k。
  2. 修改任意一个元素 k。

# 难点

可以直接使用现有的 down 和 up 两种操作来实现进阶功能吗？

注意观察 down 和 up 的操作就知道，在这个过程中，我们是不记录元素的顺序的。什么意思呢？注意两个操作中的 swap 函数，我们交换的是节点的值，而节点的值一但被交换，就可能被连续交换，最后我们不知道它在那个节点上。

为了解决这个问题，我们使用一个 映射数组 ph 来记录节点和它对应的值。

如何理解呢？

首先要理解一点，对于第 k 个插入的元素，初始时候 k 就是 idx，这是因为我们是从末尾开始插入的（具体见 insert 函数），所以我们认为初始时，h [k] 就是我们插入的值，此时它在 idx 这个位置，也就是 ph [idx]=k。思考一下，这样做的好处：我们可以通过 h [ph [idx]] 来访问到这个值。

那么，当 k 移动之后，就把它移动到对应的 idx 就可以了，这样是不是就可以完成进阶功能了呢？

其实还是不行，注意，进阶功能都是在操作 k 这个元素，那么 k 这个元素是什么呢？其实就是 h [idx]，也就是 h 中实际存储的值。

我们来结合 insert 函数来理解，在 insert 函数中，至关重要的一步是 h[++ idx] = val; ，这一步表示的含义是 新添加一个元素(++idx)到 堆h ，这个元素的下标是idx，而h[idx]是这个元素的值，初始时也是h[k] 。

我们刚才在交换的时候存储了 idx 到 k 的映射，而当我们想找到这个值的时候，也就是 h [k] 的时候，没有办法通过 k 找到 idx，换句话说就是 可以通过 ph [idx] 就是 k，而这个 k 它只是个下标，实际的值我们不知道，也就是说通过这个 k 我们找不到 idx（此 idx 非彼 idx，这个 idx 表示 k 最初对应的实际值）。

解决这个问题也很简单，即再引入一个 映射数组 hp 表示 k 与 idx 的映射，也就是 hp [k]=idx。

（PS：笔者的自言自语，这里的两个映射数组，真的较难理解，我自己也画图研究了好久，为了读者朋友们不走弯路，我下面用个直观的示例解释一下。）

假设此时的状态为 idx=6 ，将要加入一个值为 10 ，那么根据我们上面的分析可知 新加入的10 对应的初始 idx=7,k=7 ，此时我们也应该初始化 ph[7]=7,hp[7]=7 。

OK，假设，执行了一次 up 操作之后， 新加入的10 交换到了点 idx=3 这个点，那么 hp[7] 应该变成 3 ，表示点 k (7) 对应的 idx 变成了 3 ；而 ph[hp[7]] 也应该与 idx=3 的交换，表示最初 idx=7 的这个点下标 k 现在映射到了 idx=3 的这个点的 k 上。（这个例子个人觉得也不是很清晰，请往下看图。）

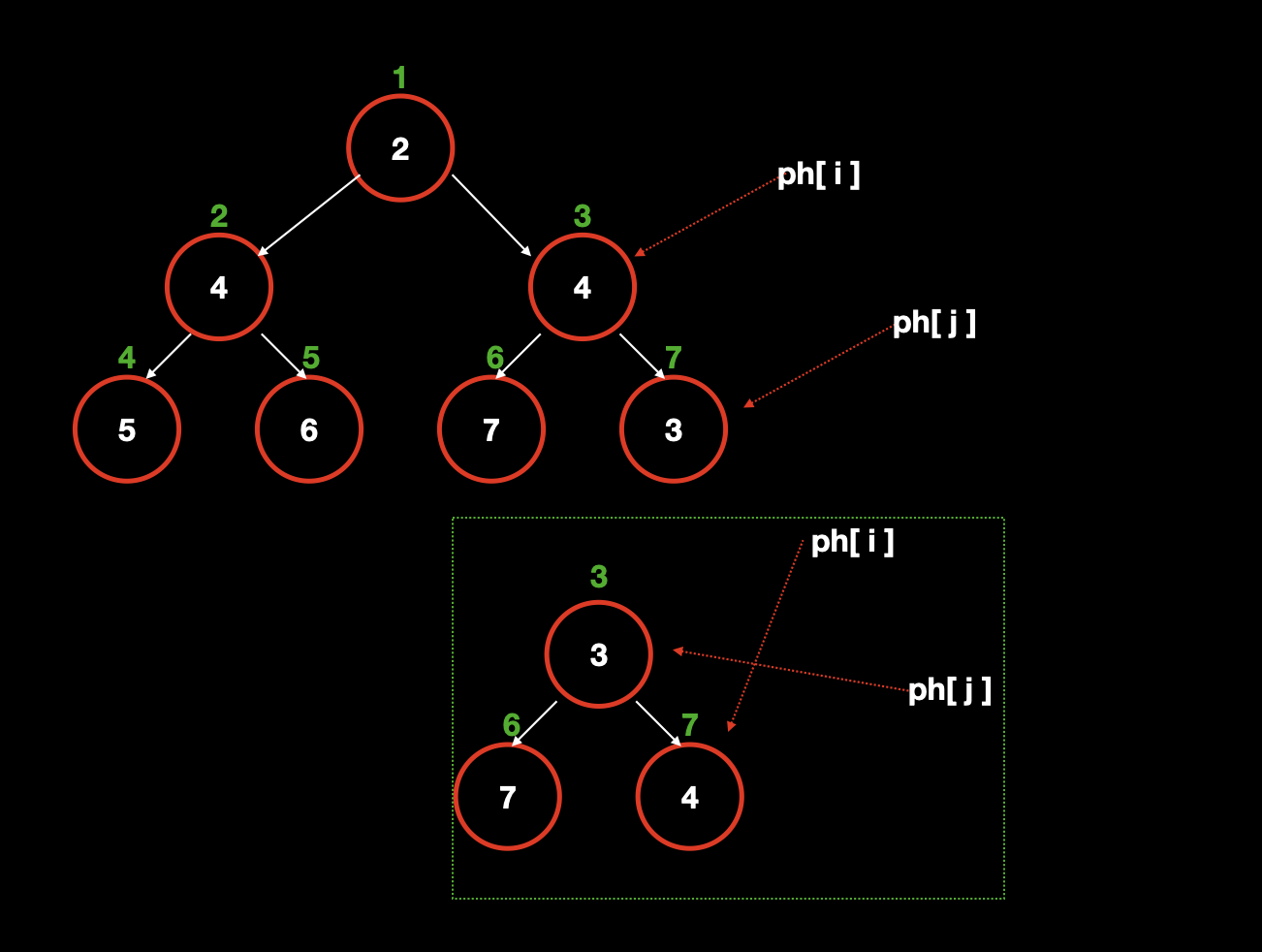
  1. 只使用 ph 数组的情况下，我们可以在图中看到，交换节点的同时，ph [idx] 指向也交换了，这样我们就能通过 idx 找到对应的值，既 idx=j 对应 3 。但是我们在进阶操作的时候，需要操作第 k 个点，比如操作 k=7 这个点，我们现在只能通过 idx 找到 k (或者叫值)，而无法知道 k=7 这个点对应的哪个 idx。

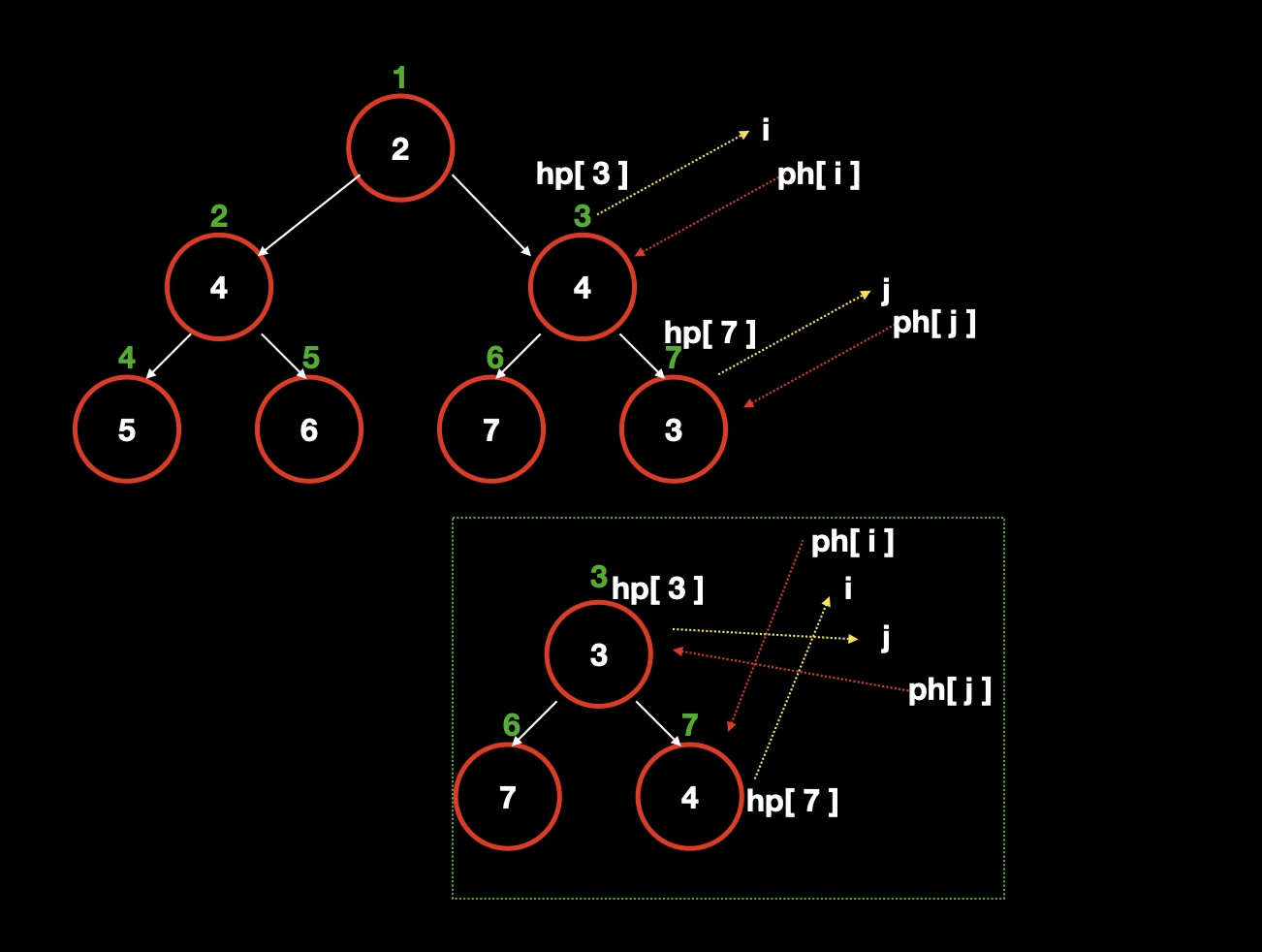
  2. 而使用了 hp 数组之后，我们就记录了 k 与 idx 的对应关系，因此当我们需要操作元素 k 的时候，就可以 hp[k] 找到 idx ，然后 h[ph[idx]] 找到这个 k 对应的值。连起来就是 h[ph[hp[k]]] 为 k 的值。

# 进阶操作的交换

在进阶操作里，我们要把标准操作中使用的 swap 函数换成我们自己的 swap。

// 其中 a、b 是两个需要交换的元素的下标
void my_swap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]); 
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

请注意，其中的前两步交换顺序不能改变，因为第一步中明显依赖了 hp 数组，所以要先交换 ph，再交换 hp。

# 对标准操作的影响

很显然，想要使用进阶操作，那么在标准操作的时候，也需要改变。

其中，down 和 up 操作中的 swap 需要换成 my_swap，并且插入函数需要做出如下改动。

void insert(int val) {
    k ++ ;
    idx ++ ;
    ph[k] = idx;
    hp[idx] = k;
    h[idx] = val;
    up(idx);
}

# 进阶操作：1. 删除第 k 个元素

操作与删除堆顶元素相同，把最后一个元素 idx 覆盖 k，然后删除最后一个元素 (idx --)，然后进行 down 或者 up。

void del(int k) {
    // 先拿到 k 对应的 idx，防止后面交换时候改变。
    k_idx = ph[k]; 
    // 交换之后，此时 ph [k] 指向堆中最后一个元素 idx，
    // 还好我们上一步保存了源 ph [k]，也就是 k_idx。
    my_swap(k_idx, idx);
    idx -- ;
    // 注意，k_idx 可能在树的中间，
    // 而执行 down 或者 up 都可以让它归位（符合堆的性质）
    // 所以，这俩函数最多只会执行一个。
    down(k_idx), up(k_idx);
}

# 进阶操作：2. 修改第 k 个元素为 x

这个就比较简单了，我们在分析中就说了 h[ph[k]] 就是 k 的值。

void update(int k, int x) {
    k_idx = ph[k];
    h[k_idx] = x;
    down(k_idx), up(k_idx);
}

大家，可能有点疑惑，在进阶操作中，好像 hp 数组没有体现出来作用啊？其实不是的，hp 数组的最大作用在于维护 k 的正确性，也就是只有在交换时候使用了 hp 数组， swap(ph[hp[a]], ph[hp[b]]) ，才能保证 h[ph[k]] 是正确的。

# 标准功能：数组建堆

如果读者堆 (heap) 用的多的话，就会知道还有一个很常用的标准功能：将数组改建成堆。

在 python 里，这个 api 是 heapq.heapify(x) ，其中 x 是数组，如果看这个 api 的介绍，你会发现这是一个线性时间内的操作。
线性时间建堆

这就奇怪了，根据我们上面分析的，每个元素的插入是 O (logn) 的复杂度，那么 n 个元素插入到堆中不就是 O (nlogn) 吗？

是的，所以这里并没有把每个元素都插入一遍，采用的建堆方法是 循环 n/2 ~ 1 执行down操作 。

for (int i = n / 2; i > 0; i -- ) {
    down(i);
}

# 建堆的正确性

思考一下上面的建堆，为什么就能将数组转换成堆呢？

这依赖完全二叉树的一个重要的性质：当完全二叉树有 n 个节点的时候，其叶子节点个数为 n/2。

这个性质有啥用嘞？因为，我们知道堆的性质，无论是大根堆还是小根堆，叶子节点都一定满足堆的性质，因为叶子节点没有子节点。也就是说这 n/2 个叶子节点已经不需要我们主动去操作了，所以我们从最后一个非叶子节点开始操作，而最后一个非叶子节点是什么呢？

我们知道最后一个叶子节点就是 n，而 n 是一定有父节点的，它的父节点就是最后一个非叶子节点，还记得我们计算父节点的方式嘛？就是用 当前节点除以 2 ，也就是 n/2 。（注意上面的 n/2 表示叶子节点的个数，而这里的 n/2 表示最后一个非叶子节点的下标。）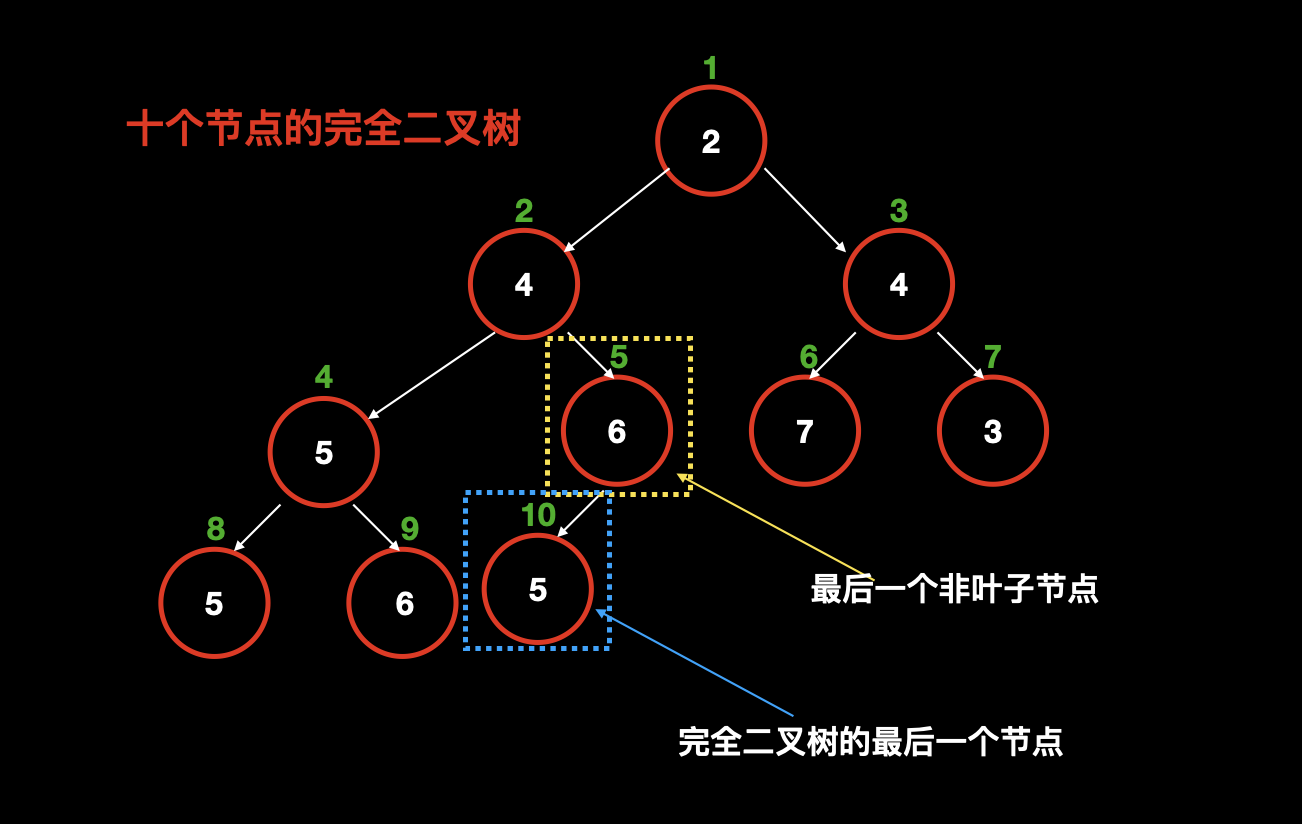

因此，我们从 最后一个非叶子节点 (n/2) 循环到 1，每次执行 down 操作，这样就让堆中的所有元素都满足堆的性质啦～

# 建堆的时间复杂度

分析时间复杂度同样需要知道一个关于完全二叉树的性质：完全二叉树除了最后一层外，其他所有层均为满节点。所以倒数第二层会有 n/4 个节点，而倒数第三层会有 n/8 个节点。

假设最坏情况，需要把 倒数第二层的 n/4 个节点 全部 down 到 倒数第一层，则需要 n/4 * 1 的时间；同理，把倒数第三层的 n/8 个节点 全部 down 到最后一层，则需要 n/8 * 2 的时间，根据以上规律，我们可以推出如下求时间复杂度的公式： n4∗1+n8∗2+n16∗3+…\frac{n}{4} * 1 + \frac{n}{8} * 2 + \frac{n}{16} * 3 + \dots

整理一下该公式，把 n 提出来：
n(122+223+324+⋯)n(\frac{1}{2^2} + \frac{2}{2^3} + \frac{3}{2^4} + \cdots)

假设：S=122+223+324+⋯S = \frac{1}{2^2} + \frac{2}{2^3} + \frac{3}{2^4} + \cdots

那么：2S=12+222+323+⋯2S = \frac{1}{2} + \frac{2}{2^2} + \frac{3}{2^3} + \cdots

然后用2S−S=S=12+122+123+⋯2S-S = S = \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + \cdots

而公式S=12+122+123+⋯S = \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + \cdots 一定是小于 1 的，所以这种建堆的时间复杂度就是 O (n) 的。

# Code

整理一下，完整的二叉堆的简易实现。

#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;
const int N = 100010;
int n;
int h[N], idx, ph[N], hp[N];
void heap_swap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}
void down(int u) {
    int t = u;
    if (u * 2 <= idx && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= idx && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t) {
        heap_swap(u, t);
        down(t);
    }
}
void up(int u) {
    while (u / 2 && h[u / 2 ] > h[u]) {
        heap_swap(u / 2, u);
        u /= 2;
    }
}
void insert(int val) {
    k ++ ;
    idx ++ ;
    ph[k] = idx;
    hp[idx] = k;
    h[idx] = val;
    up(idx);
}
void del(int k) {
    k_idx = ph[k]; 
    heap_swap(k_idx, idx);
    idx -- ;
    down(k_idx), up(k_idx);
}
int get_top() {
    return h[1];
}
void heapify(x) {
    for (int i = x.size() / 2; i > 0; i -- ) {
        down(i);
    }
}
# 总结
一般而言，各个编程语言提供的堆功能相差无几，最核心的功能就是快速的找出最值以及快速的插入一个值。而我们自定义的堆，除了满足基本操作外，还支持 “反悔”，可以根据插入的顺序删除或修改中间插入的元素。
自定义堆时候，有两个操作是狠关键的，一个是 down、一个是 up，他们都可以使某个元素符合堆的性质。
在定义进阶操作的时候，理解两个映射数组 ph、hp 是非常关键的。
理解堆的各种操作的实现，在应用的时候无疑可以起到事半功倍的效果。加油～～
END
  
 更新于   阅读次数  次
请我喝[茶]~(￣▽￣)~*
A Cat Without Sugar 微信支付
微信支付
A Cat Without Sugar 支付宝
支付宝