前置文章：有趣的博弈论问题

# 前情回顾

在文章 “有趣的博弈论问题” 中，主要描述了基础博弈论游戏的胜负结论及证明，具体是：在 “尼姆游戏” 中，如果给出所有的石子堆的个数全部异或起来不等于 0，则先手必胜；否则，必败，为了与本文后面的游戏做区分，我们将这个游戏称为标准尼姆游戏。

# 标准尼姆游戏的扩展

# 台阶 - Nim 游戏

现在，有一个 n 级台阶的楼梯，每级台阶上都有若干个石子，其中第 i 级台阶上有 ai 个石子 (i≥1)。

两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。

已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

# 分析及结论

相对于标准版的尼姆游戏，台阶版本更像是一个脑筋急转弯。

仔细思考后，可以发现一个重要的性质，最终的结果与偶数级台阶没有任何关系，也就是说这是一个由奇数台阶组成的标准版尼姆游戏。

证明：

1. 首先，要理解两个题目中隐含的信息，既然每次只能移动一阶，那么处于偶数阶层的石子，想要移动到地面上，一定需要移动偶数次。
2. 其次，游戏中规定每次可以移动任意多的石子（大于 0 个）。
3. 因此对于先手来说，只要后手将 偶数台阶的石子 移动到 奇数台阶 ，轮到先手，先手就可以 在想移动的石子基础上 把上一次 后手移动的石子原封不动的带到另一个偶数台阶 ，而我们知道最后的偶数台阶就是 0，也就是地上。
4. 所以，对于后手来说，无论怎么移动偶数台阶的石子，先手都可以在下一次移动时 顺便 带上，直到地上。因此偶数台阶无论有多少石子，都对结果无影响。
5. 现在只剩下奇数台阶上的石子，使用同标准尼姆游戏中的方式分析。
6. 最后结果中，所有的奇数台阶的石子异或起来一定为 0，我们姑且称为 平衡状态 。而如果初始的所有奇数台阶石子不是 0（非平衡状态），那么先手一定可以通过拿走一些石子使之平衡，而后手又会打破平衡，直到最后一次先手使所有奇数台阶石子达到平衡，此时所有石子都被拿到地上，后手失败。

# Code

#include <iostream>

#include <algorithm>

using namespace std;

const int N = 100010;

int nums[N];

int n;

int main () {

    cin >> n;

    int res = 0;

    for (int i = 1; i <= n; i ++ ) {

        cin >> nums[i];

        if (i & 1) res ^= nums[i];

    }

    if (res) puts("Yes");

    else puts("No");

    return 0;

}

# 集合 - Nim 游戏

给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

# 前置知识

mex 运算：用来找到一个集合中不存在的最小自然数。比如：S={1,2,3}，则 mex (S)=0，表示 0 是集合 S 中不存在的最小自然数。

SG 函数：在有向图中，假设从节点 x 出发，共有 k 条有向边，分别到达节点$y_1,y_2...y_k$ 。那么我们定义 SG (x) 为：后继节点$y_1,y_2...y_k$ 的 SG 函数值 构成的集合，再执行 mex 操作。
公式：$SG(x) = mex(\{SG(y_1), SG(y_1),...,SG(y_k)\})$
特别地，整个有向图 G 的 SG 函数值等于有向图起点 s 的 SG 函数值：$SG(G)=S G(s)$ 。
终点的 SG 为 0。

# 分析以及结论

是的，相信读者从前置知识中已经感觉到了，本题与有向图相关，而其关键就是把每个石堆中的石子能选出的状态看做一个有向图。

例如：
给出集合 S={2,5} （也就是每次只能拿走 两颗 或者 五颗 石子），并且假设此时只有一堆石子，个数为 10，我们看下该堆石子组成的有向图：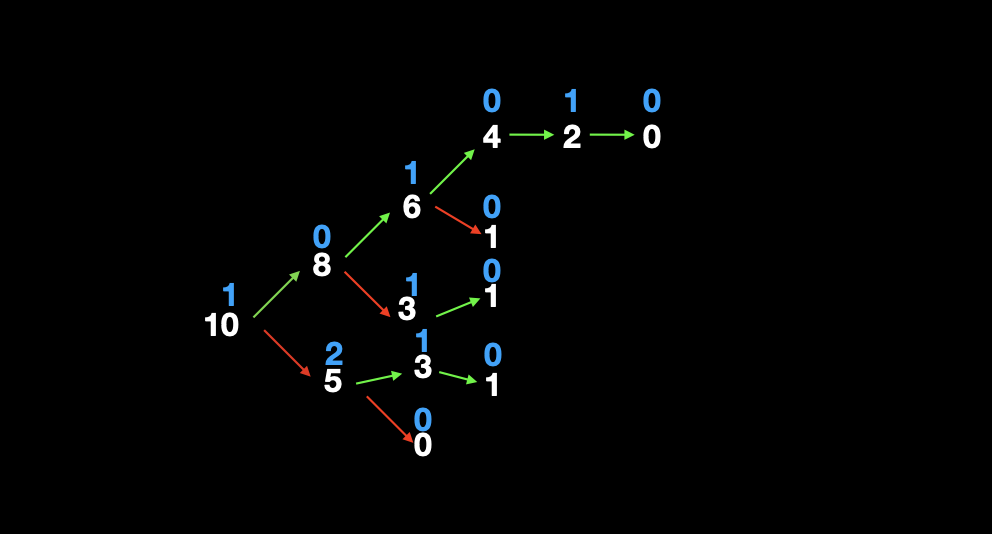

这个奇奇怪怪的图片，有如下含义：

1. 绿色有向线段：表示拿走两颗石子。
2. 红色有向线段：表示拿走五颗石子。
3. 白色数字：表示此状态下的剩余石子数。
4. 蓝色数字：表示此时 SG (x) 的值。
   1. 例如：SG (10)=mex ({0,2})，既，最小的不在集合 {0,2} 中的自然数，那么结果就是 1；
   2. 再例如：SG (4)=mex ({1})，既，最小的不在集合 {1} 中的自然数，那么结果就是 0；
   3. 再再例如：SG (5)=mex ({0,1})，既，最小的不在集合 {0,1} 中的自然数，那么结果就是 2；
   4. 自然的，没有后继节点的 SG 值均为 0。

如果能理解把一堆石子转换成有向图的操作，其实就不难 进一步 的理解如下结论：
当仅有一堆石子 h[i] 时， h[i]!=0 ，则先手必胜，否则必败。

证明：

1. 当 SG (h [i]) 不为 0 时，因为 SG 经过了 mex 运算，所以其连接的点中 必有为0的点 ，我们假设这个点是 x；当 h[i] 走到 x 时，因为 x 本身为 0，而它又经过了 mex 运算，所以 x 所连接的点也不为 0。
2. 终点的 SG 值必为 0。
3. 综合上述 1、2 两点，我们知道当先手的起始点 SG 不为 0 时，它一定有办法把为 0 的状态留给后手，而后手又会破坏该状态，直到最后一次遇到 SG 为 0 的终点，后手失败。（非常像标准尼姆游戏哦～）

再进一步的，如果从一堆石子扩展到多堆石子呢？

注意，每个玩家不再只能在一个图上走，而是可以选择任何一个图走一步。并且根据题目要求，需要在每一个图上都不能再走，才算失败。

再回忆一下标准尼姆游戏中的结论：每堆石子异或起来如果不是 0，则先手必胜；否则，必败。

根据以上结论，我们是否能推出本游戏的结论：每个图的 SG 值异或起来如果不是 0，则先手必胜呢？

一定是可以的，因为本游戏的一堆石子的 必胜态 是 SG (x) 不等于 0，我们把它看做标准尼姆游戏中的每堆石子不为 0，则可以用标准尼姆游戏的证明方式证明 本游戏的结论 。

# Code

实现上，比较重要的点是使用记忆化搜索，降低时间复杂度。

#include <iostream>

#include <algorithm>

#include <cstring>

#include <unordered_set>

using namespace std;

const int N = 110, K = 10010;

int n, k;

int s[N], f[K];

// 求状态 x 的 SG 值

int sg(int x) {

    // 记忆化搜索

    if (f[x] != -1) return f[x];

    unordered_set<int> S;

    // 枚举路线

    for (int i = 0; i < k; i ++ ) {

        int sum = s[i];

        // 如果是合法延伸范围，

        // 就把它可以延伸的子节点的 SG 加入集合

        if (x >= sum) S.insert(sg(x - sum));

    }

    //mex，找到最小的不在 S 中的自然数，就是 x 的 SG 值。

    for (int i = 0; ; i ++ ) {

        if (!S.count(i)) {

            return f[x] = i;

        }

    }

}

int main () {

    cin >> k;

    // 总共可以有 k 种取数

    for (int i = 0; i < k; i ++ ) cin >> s[i];

    cin >> n;

    memset(f, -1, sizeof f);

    int res = 0;

    //n 个石堆全部异或起来

    for (int i = 0; i < n; i ++ ) {

        int x;

        cin >> x;

        res ^= sg(x);

    }

    if (res) puts("Yes");

    else puts("No");

    return 0;

}

# 拆分 - Nim 游戏

给定 n 堆石子，两位玩家轮流操作，每次操作可以取走其中的一堆石子，然后放入两堆规模更小的石子（新堆规模可以为 0，且两个新堆的石子总数可以大于取走的那堆石子数），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

# 分析及结论

本题有几个关键点：

1. 与前两题相同，两个玩家每次操作，可以从某堆里取走任意石子；
2. 不同之处在于，本题取走的石子之后，需要放入两堆新的石子，并且 每堆数量要严格小于 本轮取走的石子数量 （注意是两个新堆，而不是放入现有的石堆）。
3. 无法再次进行操作的人视为失败。这里有一个关键问题，是否一定会结束呢？答案是肯定的，虽然石子的总数量可能会变得更多，但是最大值一直在变小，最终一定会全部变成 0。
4. 比如，把一堆 10 个石子，拆分成两堆，每堆 9 个，虽然总数变多，但是最大值变小，所以如此拆分下去，必定所有的都会变成 0。

根据上题的最后结论，当有多个石堆的时候，可以求出每个石堆的 SG 值，最后把他们全部异或起来就能得到结果。

本题，也可以使用这种方法，我们仍然把每堆石子看做一个独立的局面，求出每堆的 SG 值。

但是，每堆石子都会被拆分成两堆，这应该怎么求呢？其实把拆分后的两堆异或起来就可以了，就像最终把所有堆异或起来得到最终结果一样，把拆分的两堆异或起来，得到当前堆的结果。

# Code

#include <iostream>

#include <cstring>

#include <algorithm>

#include <unordered_set>

using namespace std;

const int N = 110;

int n;

int f[N];

int sg(int x) {

    if (f[x] != -1) return f[x];

    unordered_set<int> S;

    // 把当前石子 x，分成两堆石子 i，j

    for (int i = 0; i < x; i ++ ) {

        for (int j = 0; j <= i; j ++ ) {

            // 把两堆异或起来，得到该分支的结果

            S.insert(sg(i) ^ sg(j));

        }

    }

    //mex，找出最小的不存在于集合的自然数；

    for (int i = 0; ; i ++ ) {

        if (!S.count(i)) return f[x] = i;

    }

}

int main () {

    cin >> n;

    int res = 0;

    memset(f, -1, sizeof f);

    for (int i = 0; i < n; i ++ ) {

        int x;

        cin >> x;

        res ^= sg(x);

    }

    if (res) puts("Yes");

    else puts("No");

    return 0;

}

END