首页 算法 搜索

书接上回

# AcWing 165. 小猫爬山

翰翰和达达饲养了 N 只小猫，这天，小猫们要去爬山。

经历了千辛万苦，小猫们终于爬上了山顶，但是疲倦的它们再也不想徒步走下山了（呜咕 >_<）。

翰翰和达达只好花钱让它们坐索道下山。

索道上的缆车最大承重量为 W，而 N 只小猫的重量分别是 C1、C2……CN。

当然，每辆缆车上的小猫的重量之和不能超过 W。

每租用一辆缆车，翰翰和达达就要付 1 美元，所以他们想知道，最少需要付多少美元才能把这 N 只小猫都运送下山？

输入格式
第 1 行：包含两个用空格隔开的整数，N 和 W。

第 2..N+1 行：每行一个整数，其中第 i+1 行的整数表示第 i 只小猫的重量 Ci。

输出格式
输出一个整数，表示最少需要多少美元，也就是最少需要多少辆缆车。

数据范围

1≤N≤18,
1≤Ci≤W≤108

输入样例

5 1996
1
2
1994
12
29
**输出样例**
2

# 题目分析

有 N 只猫咪，已经限定重量的缆车，问最少需要多少个缆车可以把所有的猫咪都装上。

# 题目分析

我们可以把所有装猫咪的方法都枚举出来，这样自然就知道最少需要多少缆车。

所以需要一种搜索方案，可以枚举出所有情况。我们考虑用猫咪去匹配缆车，那么就只有两种情况，一种是猫咪可以放在现有的缆车中，另一种是猫咪不能放在现有缆车，需要开一辆新的缆车。

根据上面的分析，我们关心的状态有：

  1. u：当前安排的是第几只猫咪，如果当前所有小猫都运送完毕，说明找到了一个方案。
  2. k：现有的缆车数量，我们对于每只小猫都枚举这些缆车，看是否可以放进去。
  3. sum []：全局变量，存储每个缆车中现有的猫咪总重量。

剪枝：

  1. 把猫咪按照重量排序，先安排比较重的猫咪，占用缆车的重量就多，缆车的剩余重量少，那么后续的可选方案也就更少，这意味着决策树的分支更少。

  2. 搜索的时候发现当前的缆车数量 k 已经大于或者等于最佳方案的数量，就可以立即停止搜索了。

# Code

注意，即便当前猫咪可以放在之前的缆车中，这也不意味着放到已有缆车中更优，所以为了枚举出所有的情况，必须对于每个猫咪都尝试新开一个缆车。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20;
int cats[N], sum[N];
int n, m;
int res = N;
void dfs(int u, int k) {
    if (k >= res) return ;
    if (u == n) {
        res = k;
        return ;
    }
    for (int i = 0; i < k; i ++ ) {
        if (sum[i] + cats[u] <= m) {
            sum[i] += cats[u];
            dfs(u + 1, k);
            sum[i] -= cats[u];
        }
    }
    sum[k] = cats[u];
    dfs(u + 1, k + 1);
    sum[k] = 0;
}
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i ++ ) cin >> cats[i];
    sort(cats, cats + n);
    reverse(cats, cats + n);
    dfs(0, 0);
    cout << res << endl;
    return 0;
}
# AcWing 166. 数独
数独 是一种传统益智游戏，你需要把一个 9×9 的数独补充完整，使得数独中每行、每列、每个 3×3 的九宫格内数字 1∼9 均恰好出现一次。
请编写一个程序填写数独。
输入格式
输入包含多组测试用例。
每个测试用例占一行，包含 81 个字符，代表数独的 81 个格内数据（顺序总体由上到下，同行由左到右）。
每个字符都是一个数字（1−9）或一个 .（表示尚未填充）。
您可以假设输入中的每个谜题都只有一个解决方案。
文件结尾处为包含单词 end 的单行，表示输入结束。
输出格式
每个测试用例，输出一行数据，代表填充完全后的数独。
输入样例
4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......
......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
end

输出样例
417369825632158947958724316825437169791586432346912758289643571573291684164875293
416837529982465371735129468571298643293746185864351297647913852359682714128574936

# 题目描述
数独游戏不知道大家小时候有没有玩过呢？数独游戏的规则是使用数字 1~9 填充由 3*3 的小矩阵构成的 9*9 的大矩阵，填充的规则是：每个 3*3 的小格子中的数字不能重复，每行的数字不能重复，每列的数字不能重复。要求输出填充完的结果。
# 题目分析
对于每个小方格，理论上都有九个数字可以填充，所以对于每个小方格我们都考虑所有可以填充的数字，如果符合规则，我们就填进去，使用 DFS 枚举出所有的情况，最后一定可以填充完成。
但是我们可以观察到，极限情况下，会有 81 个格子，每个格子都有九种选择，只使用 DFS 爆搜时间复杂度来到恐怖的O(981)O(9^{81}) ，相信量子计算机出来之前是不太能接受了，因此必须进行剪枝：
  1. 优化搜索的顺序。最常用的剪枝之一，本题中，虽然理论上可以选择任意位置填数字，但是考虑后续分支的数量，一定是选择当前可选数字最少的位置，这样留给后续的分支也会更少。
  2. 选择了一个位置放数字后就可以直接进入下一层，而不需要把其他位置都选择上。我们可以通过回溯，来枚举出所有的方案。
  3. 需要频繁的判断某个数字是否可以放到某个格子，为了加速判断，我们可以使用位运算来进行优化。因为总共有九位数字，所以我们可以用一个九位的二进制数来存储，某个数字有没有被使用过，例如： 101011000 ，即可表示 24789 这几个数字已经被使用。
# Code
涉及到二进制运算的有几个点：
  1. 需要每次搜索，需要找到当前可选数字最少的格子。如何判断某个格子的可选数字呢？可以把三个二进制数字取并集，也就是做 & 操作。这样结果为 1 的二进制位就是可以选的数字。
  2. 我们可以用 lowbit 操作统计某个二进制数字有多少个 1。
  3. 为了快速找到某个二进制位的 1 的数量，我们可以先预处理出一个数组来存储每个数字 1 的数量。
  4. 为了快速找到最后一个 1 的位置，也就是需要操作的格子，我们可以使用一个数组来存放每个二进制数对应的最后一个 1 的位置。
考虑是否需要回溯？
因为对于每个格子，我们都要尽可能把所有可选的数字枚举到，所以需要回溯。
考虑是否需要判重数组？
因为我们使用三个二进制数字来存储每个格子的状态，而状态中已经可以表示哪个数字用了，哪个数字还没被使用。所以不再需要额外的判重数组了。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 9;
//cell 存储的是当前格子在哪个 以 3*3 为单位的小矩阵中
int row[N], col[N], cell[3][3];
char str[100];
//ones [i] 表示 i 中有几个 1 用来快速找到 1 最少的那个格子
//map [i] 表示最后的一个 1 后面有几个 0 也就是 i 的最后一个 1 在第几位。
// 比如 lowbit 返回二进制 (1000) 那么结果就是 8 而 map 则存储 map [8] = 3
int ones[1 << N], map[1 << N];
//inline 可以直接把函数体直接放到调用的部分 省去调用函数的开销
inline int lowbit(int x) { // 返回最后一个 1 
    return x & -x;
}
// 初始化 行列格 的选择状态 为全部可选。
void init() {
    for (int i = 0; i < N; i ++ ) row[i] = col[i] = (1 << N) - 1;
    for (int i = 0; i < 3; i ++ ) 
        for (int j = 0; j < 3; j ++ )   
            cell[i][j] = (1 << N) - 1;
}
// 求可选方案的交集
inline int get(int x, int y) {
    return row[x] & col[y] & cell[x / 3][y / 3];
}
bool dfs(int cnt) {
    if (!cnt) return true;
    // 找出可选方案数最小的格子
    int minv = 10;
    int x, y;
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j < N; j ++ ) {
            if (str[i * N + j] == '.') { // 如果格子可选
                int t = ones[get(i, j)];
                if (t < minv) {
                    minv = t;
                    x = i, y = j;
                }
            }
        }
    // cout << x << ' ' << y << endl;
    for (int i = get(x, y); i; i -= lowbit(i)) {
        int t = map[lowbit(i)];
        // 修改状态 把最后一个 1 变成 0
        row[x] -= 1 << t;
        col[y] -= 1 << t;
        cell[x / 3][y / 3] -= 1 << t;
        //x * 9 + y 把二维坐标转换成一维中的位置
        str[x * 9 + y] = '1' + t;
        if (dfs(cnt - 1)) return true;
        // 回溯
        row[x] += 1 << t;
        col[y] += 1 << t;
        // 在从一维中的位置 转换到二维坐标
        cell[x / 3][y / 3] += 1 << t;
        str[x * 9 + y] = '.';
    }
    return false;
}
int main() {
    for (int i = 0; i < N; i ++ ) map[1 << i] = i;
    for (int i = 0; i < 1 << N; i ++ ) {
        int s = 0;
        for (int j = i; j; j -= lowbit(j)) s ++ ;
        ones[i] = s; //i 的二进制表示中有 s 个 1
    }
    while (cin >> str, str[0] != 'e') {
        init();
        int cnt = 0;
        for (int i = 0, k = 0; i < N; i ++ ) 
            for (int j = 0; j < N; j ++, k ++ ) 
                if (str[k] != '.') {
                    int t = str[k] - '1';
                    str[i * N + j] = t + '1';
                    int v = 1 << t;
                    row[i] -= v;
                    // 2022 年 8 月 8 日 把 col [j] 写成了 col [i] 找了一个半小时 
                    // 晚 23:40 终于找到了
                    col[j] -= v;
                    cell[i / 3][j / 3] -= v;
                }
                else cnt ++ ; // 没填的格子总共有 cnt 个
        dfs(cnt);
        cout << str << endl;
    }
    return 0;
}
# AcWing 167. 木棒
乔治拿来一组等长的木棒，将它们随机地砍断，使得每一节木棍的长度都不超过 50 个长度单位。
然后他又想把这些木棍恢复到为裁截前的状态，但忘记了初始时有多少木棒以及木棒的初始长度。
请你设计一个程序，帮助乔治计算木棒的可能最小长度。
每一节木棍的长度都用大于零的整数表示。
输入格式
输入包含多组数据，每组数据包括两行。
第一行是一个不超过 64 的整数，表示砍断之后共有多少节木棍。
第二行是截断以后，所得到的各节木棍的长度。
在最后一组数据之后，是一个零。
输出格式
为每组数据，分别输出原始木棒的可能最小长度，每组数据占一行。
数据范围
数据保证每一节木棍的长度均不大于 50。
输入样例
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0

输出样例
6
5

# 题目描述
有一组长度相等的木棒，具体多长我们不知道，把它们随机的砍断成长度不超 50 的木棍。现在，我们的目标是把这些木棍再恢复成长度相等的木棒。问 最小的木棒的可能长度是多少。
# 题目分析
比较明显的一个爆搜题目，木棒的长度一定是有一个最大限度的，即原本只有一根木棒，长度是所有木棍长度总和。
（我们约定，多跟木棍组成木棒，木棍的长度由题目给出。）
既然木棒长度一定是有限的，那么我们可以从 1 开始枚举木棒的长度，只要木棒能被 总长度 平分，我们就试着看能不能把所有的木棍都拼接上。
具体的，我们可以每次使用一个木棒，来检查所有的木棍，只要木棒的长度还没到极限，就把木棍拼接上，如果当前木棒已经拼接完成了，就新开一根木棒，继续检查所有的木棍，以此类推，直到把所有的木棍拼接完，就找到了答案。
为了加快搜索速度，我们来分析一下可以进行剪枝的点：
  1. 同上题一样，对于搜索顺序，我们搜索更大的木棍，就可以留出更小的空间给后续选择，也就意味着后续分支会更少，所以可以先对所有的木棍排序。
  2. 另外一个比较明显的剪枝是：因为木棍已经是有序的，那么如果当前木棍不能拼接在当前木棒上，那么和当前木棍相同长度的也不能拼接到当前木棒上，直接跳过即可。
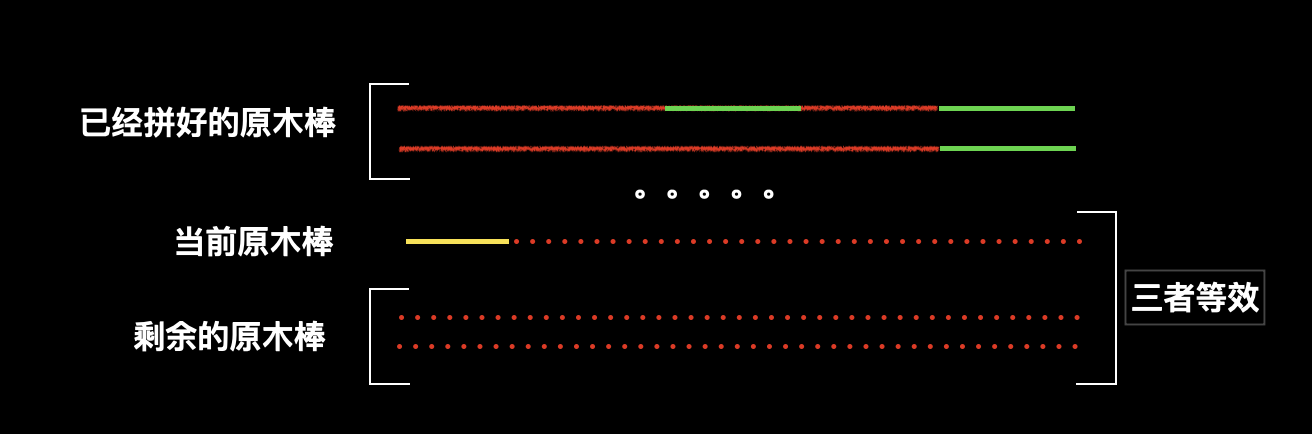
  3. 还有一个不明显的剪枝是：当前组合失败时，当前木棍是第一根组成木棒的木棍，说明当前方案直接失败，因为后续的空木棒也是没有任何木棍组成的，而当前木棍作为这个空木棒的第一根组成木棍失败，再其他空木棒作为第一根组成木棍也会失败。
  4. 另外一个不明显的剪枝是：当前组合失败时，当前木棍是最后一根组成木棒的木棍，同样说明该方案直接失败。
    该结论可以使用反证法证明：假设当前处于最后一根的木棍拼在当前木棒中，我们称为原状态，而原状态失败，但是把该木棒拼在后面又可以成功了，那说明原状态中本来拼在后面的一定有一段木棍组合与当前的最后一根是完全相等的长度，那么把他们调换一下也是可以的，那样原状态应该也是成功的，但是在假设中原状态是失败的。
# Code
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 70;
int w[N], sum, length; //sum 所有木棒总长 length 单根木棒长度
bool st[N];
int n;
// 第 u 个木棒 当前木棒的长度为 s 组成这根木棒的木棍起始下标为 start
bool dfs(int u, int s, int start) {
    //u 个长度为 len 的等长木棒 总和等于 所有木棒长度总和 则找到了方案
    if (u * length == sum) return true;
    // 当前木棒的长度为 length 则新开一个木棒。
    if (s == length) return dfs(u + 1, 0, 0);
    for (int i = start; i < n; i ++ ) {
        if (st[i] ) continue;
        // 当前木棍不行 就换后面小的。
        if (s + w[i] > length) continue;
        st[i] = true;
        if (dfs(u, s + w[i], i + 1)) return true;
        st[i] = false;
        // 如果木棒的第一根木棍失败， 则后面的也一定失败
        // 如果当前木棒放在最后一个失败，则当前方案也一定失败
        if (!s) return false;
        if (s + w[i] == length) return false;
        // 剪枝 当前后两根木棍 长度相同的话 前一根木棍不能放进木棒
        // 那么后一根也不能放 所以我们可以跳过相同长度的木棍。
        int j = i;
        while (j < n and w[j] == w[i]) j ++ ;
        i = j - 1;
    }
    return false;
}
int main() {
    while (cin >> n, n) {
        memset(st, 0, sizeof st);
        sum = 0;
        for (int i = 0; i < n; i ++ ) {
            cin >> w[i];
            sum += w[i];
        }
        // 把木棍从大到小排列 这样每次枚举大的 剩下的空间小 分支少
        sort(w, w + n);
        reverse(w, w + n);
        length = 1;
        while (true) {
            // 剪枝 1
            if (sum % length == 0 and dfs(0, 0, 0)) {
                cout << length << endl;
                break;
            }
            length ++ ;
        }
    }
    return 0;
}
# AcWing 168. 生日蛋糕
7 月 17 日是 Mr.W 的生日，ACM-THU 为此要制作一个体积为 Nπ 的 M 层生日蛋糕，每层都是一个圆柱体。
设从下往上数第 i 层蛋糕是半径为 Ri，高度为 Hi 的圆柱。
当 i<M 时，要求 Ri>Ri+1 且 Hi>Hi+1。
由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积 Q 最小。
令 Q=Sπ ，请编程对给出的 N 和 M，找出蛋糕的制作方案（适当的 Ri 和 Hi 的值），使 S 最小。
除 Q 外，以上所有数据皆为正整数。
输入格式
输入包含两行，第一行为整数 N，表示待制作的蛋糕的体积为 Nπ。
第二行为整数 M，表示蛋糕的层数为 M。
输出格式
输出仅一行，是一个正整数 S（若无解则 S=0）。
数据范围
1≤N≤10000,
1≤M≤20

输入样例
100
2

输出样例
68

# 题目描述
想要做一个最多 M 层的蛋糕，限定体积，在不算底部的情况下，使得蛋糕的表面积最小。蛋糕最下层开始往上，每层的半径和高度都要大于上一层。所以，这个蛋糕就是如下样子滴（为了使层数越大，半径和高度越大，我们从底到顶按照大到小的顺序编号）。
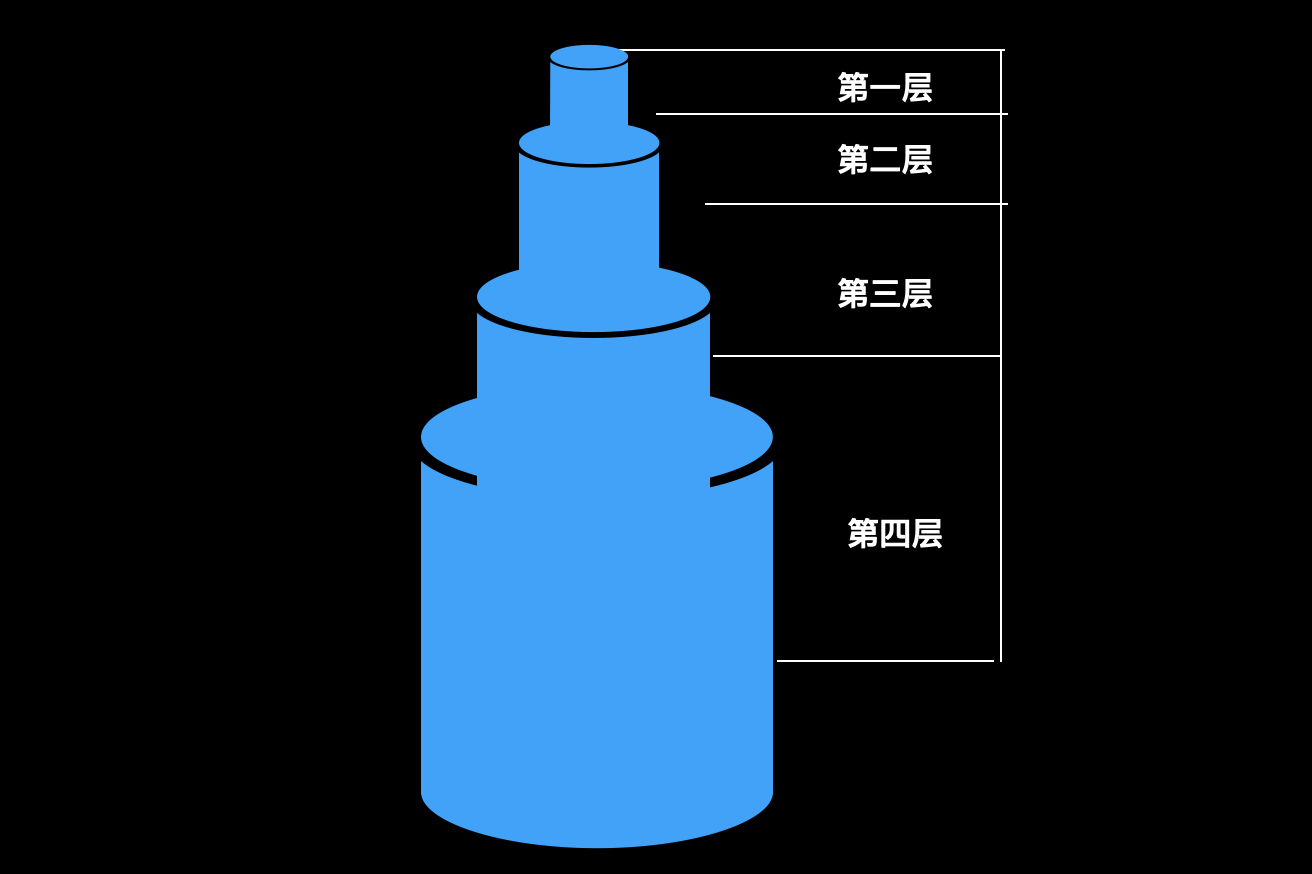
# 题目分析
从图中可以观察并推导得到的题目信息如下：
  1. 外表面积 Q 分为两部分，一部分是最下层圆柱的圆形面积，另一部分是每个圆柱体展开成长方形之后的侧面积之和。也就是：
    Q=πR42+2πR4h4+2πR3h3+2πR2h2+2πR1h1Q = \pi R_4^2 + 2\pi R_4h_4 + 2\pi R_3h_3 + 2\pi R_2h_2 + 2\pi R_1h_1
    而题目中给出Q=SπQ=S\pi，所以可以同时两面约掉π\pi，于是得到S=R42+2R4h4+2R3h3+2R2h2+2R1h1S = R_4^2 + 2 R_4h_4 + 2 R_3h_3 + 2 R_2h_2 + 2 R_1h_1。
  2. 给定总体积 N，和总层数 M，求最小的 S，也就是求使 S 最小的 R 和 H。
  3. 总体积的计算是圆形的面积乘以高度也就是：V=R42∗h4+R32∗h3+R22∗h2+R12∗h1V=R_4^2 * h_4 + R_3^2 * h_3 + R_2^2 * h_2 + R_1^2 * h_1。
  4. 从最上层往下，每一层的半径和高度都是严格递增的。
所以我们可以枚举出所有的 R 和 H 来找到最佳的方案。
按照从下向上的顺序搜索，我们需要记录以下信息：
  1. dep: 当前搜索的是哪一层；
  2. s，v: 当前总共使用了的表面积和体积；
  3. h，r：记录每层所使用的高度和半径；
剪枝：
  1. 上下界剪枝。根据题目信息 4，如果每层的半径和高度至少是 1，那么当前 dep 层的半径和高度就至少要大于等于 dep，并且小于等于Rdep+1−1R_{dep+1}-1 和Hdep+1−1H_{dep+1}-1。
    除此之外，还要考虑到体积的影响，如果当前体积是 v，而总体积是 V，那么所剩下的可用体积就是V−vV-v，所以当前层最大的体积不能超过这个值，也就是Rdep2∗hdep<V−vR_{dep}^2 * h_{dep} < V - v，而其中hdeph_{dep} 的最小取值是 1 ，所以RdepR_{dep} 的最小取值就是V−v\sqrt{V-v}，所以HdepH_{dep} 的最小取值就是(V−v)/R2(V-v)/R^2。
    综上所述，我们可以得到每层的 R 和 H 的取值：
    R∈[dep,min(V−v,Rdep+1−1)]R\in [dep, min(\sqrt{V-v}, R_{dep+1}-1)],
    H∈[dep,min((V−v)/R2,Hdep+1−1)]H\in [dep, min((V-v)/R^2, H_{dep+1}-1)]。
  2. 优化搜索顺序，我们使用倒序枚举，因为越靠近底层，则占用的面积和体积越大，留给上层的也就越小，决策树的分支也越少。
    同理，R 和 H 的枚举也要从大到小，并且因为 R 对表面积的影响比较大，所以先枚举 R。
  3. 可行性剪枝。我们可以预处理出来每层最小的可使用面积 mins[] 和体积 minv[] ，这样，如果当前的已使用体积加上当前层的最小体积超过了总体积 V，就可以剪枝；如果当前已使用的表面积加上当前层的表面积超过了答案（也就是当前最优选择的表面积），也可以直接剪枝。
  4. 最优性剪枝。
    先来看一下当前 1~dep 层的表面积公式 (忽略π\pi)：S1∼dep=∑k=1dep2∗Rk∗HKS_{1\sim dep}=\sum_{k=1}^{dep} 2*R_k*H_K；
    再来看一下当前 1~dep 层的体积公式：V−v=∑k=1depRk2∗HkV-v=\sum_{k=1}^{dep} R_k^2*H_k。
    现在来找一下这两个公式之间的关系，我们对S1∼depS_{1\sim dep} 做一个等效变形，将公式中的 2 提到前面，然后除以一个Rdep+1R_{dep+1}，再乘以一个Rdep+1R_{dep+1}，也就是变成这样：S1∼dep=2Rdep+1∑k=1dep2∗Rk∗HK∗Rdep+1S_{1\sim dep}=\frac{2}{R_{dep+1}} \sum_{k=1}^{dep} 2*R_k*H_K*R_{dep+1}。
    因为 R 是递减的，所以Rdep+1>RkR_{dep+1}>R_k，所以上述公式把后面的Rdep+1R_{dep+1} 替换成RkR_k，得到S1∼dep>2Rdep+1∑k=1dep2∗Rk2∗HKS_{1\sim dep}>\frac{2}{R_{dep+1}} \sum_{k=1}^{dep} 2*R_k^2*H_K。
    此时，我们神奇的发现，表面积公式S1∼depS_{1\sim dep} 的后半部分就是体积公式∑k=1depRk2∗Hk\sum_{k=1}^{dep} R_k^2*H_k。
    因此，我们就可以得到：S1∼dep>2∗(V−v)Rdep+1S_{1\sim dep}>\frac{2*(V-v)}{R_{dep+1}}。
    加上下一层的表面积 s，就一定有：s+S1∼dep≥2∗(V−v)Rdep+1s + S_{1\sim dep}\ge \frac{2*(V-v)}{R_{dep+1}}（其中 s 为下一层的表面积，在边界条件下可以取到等于，也就是在最后一层时，两面都是 0）。
# Code
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 25, INF = 1e9;
int V, m;
int minv[N], mins[N]; // 每层面积和体积的最小值
int R[N], H[N]; // 每层的半径和高度
int res = INF;
void dfs(int dep, int v, int s) {
    // 剪枝 3
    if (v + minv[dep] > V) return ;
    if (s + mins[dep] >= res) return ;
    // 剪枝 4
    if (s + 2 * (V - v) / R[dep + 1] >= res) return ;
    if (!dep) {
        if (v == V) res = s;
        return ;
    }
    // 枚举当前层的 r 和 h，剪枝 1 和剪枝 2
    for (int r = min(R[dep + 1] - 1, (int)sqrt(V - v)); r >= dep; r -- ) {
        for (int h = min(H[dep + 1] - 1, (V - v) / r / r); h >= dep; h -- ) {
            // cout << r << h << endl;
            int t = 0;
            // 注意如果是最底层需要把上面的圆形面积也加上
            if (dep == m) t = r * r;
            R[dep] = r;
            H[dep] = h;
            // 加上当前体积和当前表面积
            dfs(dep - 1, v + r * r * h, s + 2 * r * h + t);
        }
    }
}
int main() {
    cin >> V >> m;
    // 剪枝 3 初始化
    for (int i = 1; i <= m; i ++ ) {
        // 每层半径和高度最小值都等于当前层数
        minv[i] = minv[i - 1] + i * i * i;
        mins[i] = mins[i - 1] + 2 * i * i;
    }
    // 其中有一步要用到 R 和 H 的上一层 - 1
    // 所以我们初始化一个哨兵，方便操作
    R[m + 1] = H[m + 1] = INF;
    dfs(m, 0, 0);
    if (res == INF) res = 0;
    cout << res << endl;
    return 0;
}
# 总结
  1. 什么时候可以考虑使用深度优先搜索？
    有一个重要的条件，就是数据范围比较小，观察我们两篇文章中的九个题目，数据范围全部在 100 以下。这种数据范围下，我们有可能通过枚举出所有的方案，来找到题目要求的最佳方案。
  2. 深度优先搜索的两种常用搜索顺序。
    1. 对于物品来枚举组。物品作为递归函数的参数，在递归函数中，尝试把物品放在每个组中。
      例如：考虑一堆水果，要把他们分到不同的篮子里面，我们可以考虑每个水果放在哪个篮子里面。
      这种情况，一般需要用全局变量记录每个组的内部情况。递归的参数除了记录第几个物品之外，还要记录当前共枚举了多少物品，用来判断递归终止条件。
      参考题目：AcWing 165. 小猫爬山。
    2. 对于组来枚举物品。组作为递归函数的参数，在递归函数内部中，枚举每个物品，尝试把所有的物品都放到当前组中。
      例如：考虑一堆水果，要把他们分到不同的篮子里面，我们可以考虑用每个篮子去装所有的苹果。
      这种情况，一般需要一个判重数组，来记录哪个物品已经被使用，因为对于每一个组，都要枚举所有物品。并且，除了当前组作为函数的参数之外，还要把当前组的状态也作为函数的参数。
      参考题目：AcWing 167. 木棒
  3. 剪枝。深度优先搜索的时间复杂度是指数级别的，所以就算数据范围通常比较小，但是时间复杂度依然会非常大，所以一般都要配合剪枝。
    1. 搜索顺序的剪枝。从大往小搜索，给后续留下的可选范围越小，后续的分支就越少，搜索速度越快。
    2. 排除等效冗余。如果决策树中当前节点延伸出的几条分支具有等效性，则只需要搜索其中一条剪枝就行。
    3. 可行性剪枝。有些问题可以预处理出来一些状态，利用这些状态在搜索的过程中直接剪枝。
    4. 最优性剪枝。如果当前花费的代价已经超过了最优解，则直接剪枝。
END