# 贪心算法
贪心算法是最常见的算法之一,并且是为数不多的可以从名字上体现思想的算法。
可以用这种算法解决的问题,常常是证明难度较大,但是代码好写的问题。
# 什么样的问题可以使用贪心思路
贪心算法体现的地方在于,该算法只考虑当前的状态下的最优结果,而不是去从全局思考问题,这就是贪心两个特性之一具有最优局部结构。
并且在贪心算法中已经确定的结果,就不可被其后的状态再次影响,也就是两个关键特性中的另外一个无后效性。
# 贪心和动态规划的区别
# 解决的问题类型不同
一个比较明显的区别是,贪心算法不依赖子问题,而动态规划的状态转移是通过子问题一步步转移到最终问题 。
# 一个简单的例子
有一些不同种类商品,我有一些钱,想买尽可能多的种类的商品。 此时就可以使用贪心算法,因为我想买尽可能多种类的商品,所以我每次都买价格最便宜的那个种类,一定可以买到尽可能多种类的商品。
注意,在这个例子中,我们每次买的都是最便宜的,符合当前的 局部最优选择 ,并且我在之后每次的买进,都不会影响到我以前买到的商品,满足 无后效性 。
那如果是上面的问题再扩展一下, 给商品一个体积的概念,并且我只有一个背包,要求在不超过背包容量的情况下,买到更多种类的商品。 此时,还能每次都买价格最便宜的吗?明显不可以,因为便宜的物品是有可能占用更多的背包容量的。此时就应该使用动态规划,参考 01 背包问题。
# 经典题目
# 问题 1:LeetCode 455. 分发饼干
# 题目描述
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g [i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s [j] 。如果 s [j] >= g [i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
# 简单分析
题目最终的目的是 满足尽可能多的孩子的胃口 ,并且饼干的大小也是不一样的,那么我们很容易想到让较小的饼干满足较小胃口的孩子,这就是贪心思路。
# 证明
- 假设
g1<g2,那么当前饼干 s1,无法满足 g1 的话,肯定也无法满足 g2; - 而如果
s1<s2,我们应该先给 s1,因为 s1 满足不了,可能 s2 是有可能可以满足的;
# Code
- 先排序两个数组;
- 两个指针,一个是胃口指针,一个是饼干指针。如果当前饼干满足胃口,则两个指针同时移动,表示这块饼干给了这个孩子;无法满足胃口,则饼干指针移动,寻找更大的饼干,给这个孩子。
def findContentChildren(g, s): | |
g.sort() | |
s.sort() | |
i = j = cnt = 0 | |
while i < len(g) and j < len(s): | |
if g[i] <= s[j]: | |
i += 1 | |
cnt += 1 | |
j += 1 | |
return cnt |
# 问题 2:AcWing 148. 合并果子(哈夫曼树)
# 题目简述
在一个果园里,达达已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。他决定将所有的果子都合成一个堆。
每个堆都有自己的重量,每次能合并两个堆,合并的代价是两个堆的重量之和,请求出将所有果堆合并成一个堆的最小代价。
比如:有三个堆 1,2,9。
那么最小代价的合并方式是,先合并 1 和 2,代价是 3 ,再合并 3 和 9,代价是 12 ,花费的总代价是 3+12=15 。
# 简单分析
哈夫曼树是最经典的贪心问题(可能没有之一)。
在题目中,每次能合并两堆果子,则每次两两合并后一定有以下情况: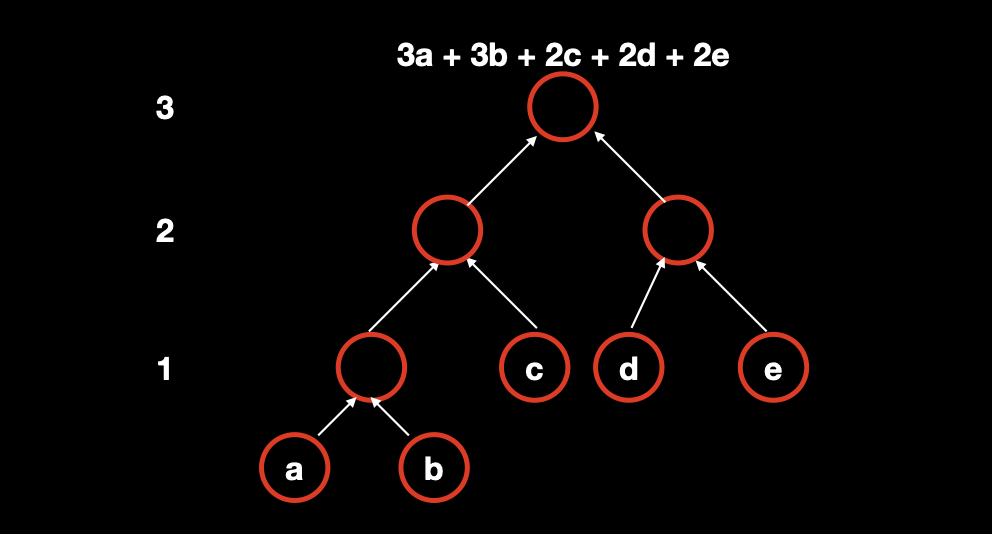
通过上图可以看出每个叶子节点的计算次数正是它到根节点的距离。
以示例中的例子举例: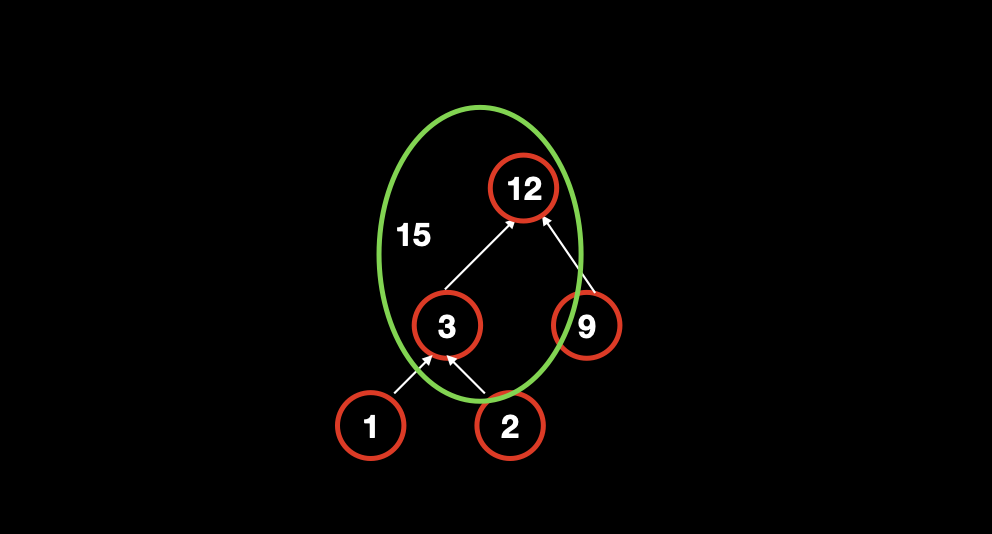
最终结果是 15,其中节点 1 和节点 2 分别被计算了两次,节点 9 被计算了一次。
通过上面的结论可以看出,越排在前面的数计算的次数越多,那么我们让更小的数计算更多次,结果一定比更大的数计算同样多次更优。
因此,我们可以使用堆这个数据结构,每次都选出最小的两个数合并,同时把合并的结果累加起来,合并到一个值之后,就是我们要的结果。
# Code
n = int(input()) | |
nums = list(map(int, input().split())) | |
import heapq | |
heapq.heapify(nums) | |
res = 0 | |
while len(nums) > 1: | |
a = heapq.heappop(nums) | |
b = heapq.heappop(nums) | |
res += a + b | |
heapq.heappush(nums, a + b) | |
print(res) |
# 问题 3:AcWing 905. 区间选点
# 题目简述
给定 N 个闭区间 [ai,bi],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
# 简单分析
举例描述一下题意: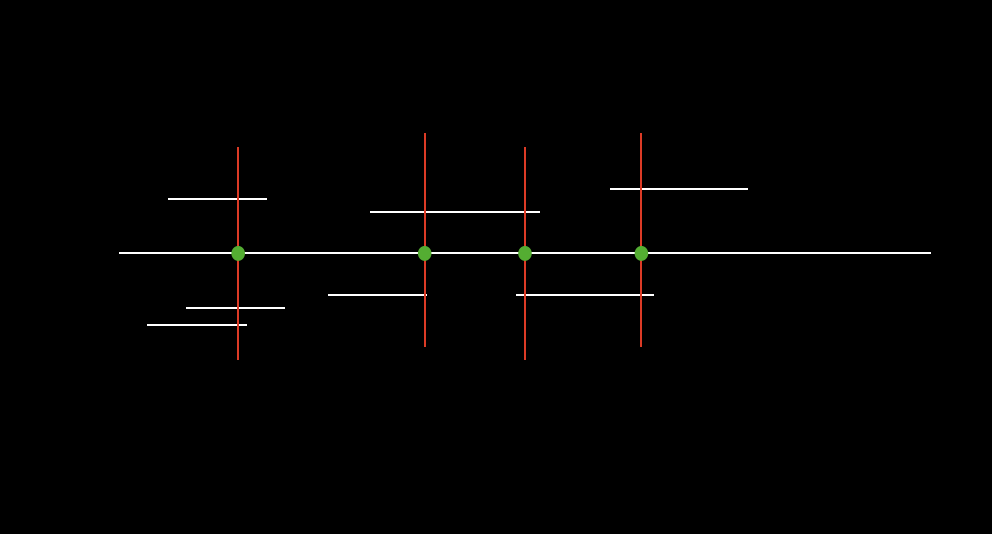
从图中可以明显看出,要使每个区间都包含一个选中的点,至少需要四个点。
这里贪心的思路是将所有的区间按照右端点从小到大排序,然后从前往后扫描,以第一个区间的 右端点 为基准点,只要当前区间无法覆盖上一区间的基准点,说明需要新增加一个选点,并且把基准点设置为当前区间的 右端点 。
# 贪心证明
假设, res 为最终的答案, cnt 为各种选点方案,那么可以明显发现 res<=cnt ,也就是最终答案,一定在所有方案之内。
而根据上面的贪心思路,出现当前区间无法覆盖到上一个基准点的时候,就要新增一个选点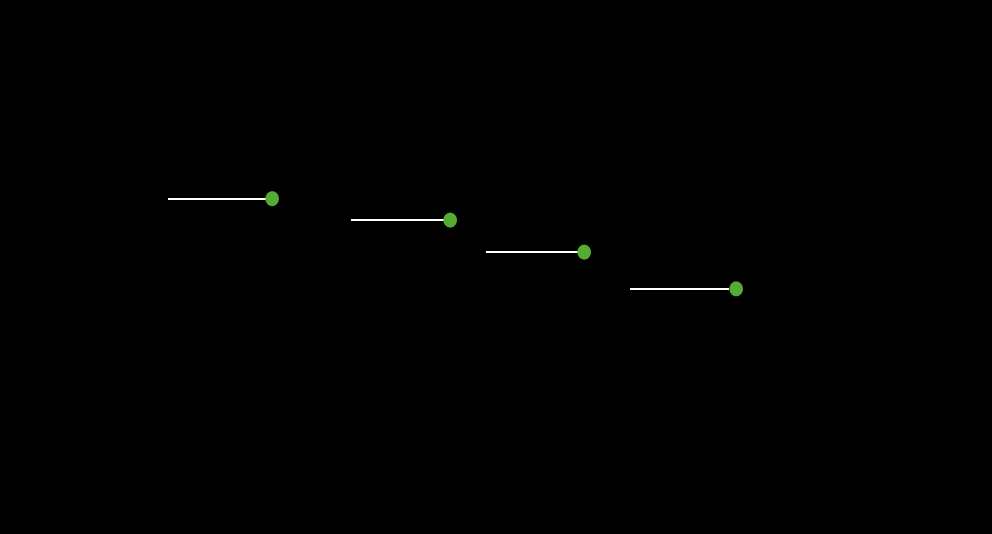
这样,当区间与区间之间没有交集的时候,就出现了需要覆盖 cnt 个区间,则至少需要 cnt 个点, 因为每个区间至少需要一个点来覆盖 。(注意这里不是取极端情况,而是为了证明贪心思路的正确性)
那么,从上面的结论我们可以推出,至少需要 cnt 个点,说明 res>=cnt ,那么结合最初的 res<=cnt ,我们就推出了 res==cnt ,也就说明我们的贪心思路可以得到最优解。
# Code
n = int(input()) | |
nums = [] | |
for _ in range(n): | |
a, b = list(map(int, input().split())) | |
nums.append((a, b)) | |
# 根据右端点排序 | |
nums.sort(key=lambda x: x[1]) | |
res = 1 | |
minn = nums[0][1] # 基准点 | |
for i in range(1, n): | |
# 左端点大于基准点 说明一定无法覆盖 | |
if nums[i][0] > minn: | |
res += 1 | |
minn = nums[i][1] | |
print(res) |
# 问题 4:AcWing 906. 区间分组
# 题目简述
给定 N 个闭区间 [ai,bi],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
# 题目分析
在上一题 (Acwing 905. 区间选点) 中, 产生交集 的区间可以计数为 1 ,而在本题中, 不产生交集 的区间才可以计数为 1 。
本题贪心的思路是先根据左端点从小到大排序。然后从前往后扫描,因为此时当前区间的左端点一定大于等于前面区间的左端点,那么只要此时它的左端点再大于前面某个组里的最大右端点,那么当前区间就能加入那个组。
用示例举例:
示例给出的例子是 [-1, 1], [2, 4], [3, 5] 。先按照左端点排序。
从前往后扫描把 [-1, 1] 放到 第一个组 ,继续扫描到区间 [2, 4] ,因为已经排序好,所以左端点 2 已经是最大的左端点,又有左端点 2 大于 第一个组 的最大右端点 1 ,所以当前区间一定和 第一个组 的所有区间都没有交集,也就是可以放到第一个组。
# 贪心证明
参考上一题的证明。
假设, res 为最终的答案, cnt 为各种分组方案,那么一定有 res<=cnt 。然后我们又可以证明出当 cnt 个区间有共同交点的时候,就至少需要 cnt 个组,因此 res>=cnt 。由此推出 res==cnt 。
# Code
在实现上,我们如何判断出,当前的左端点是不是可以小于某个组的最大右端点呢?
其实只要每次左端点都和 最小的最大右端点 比较就可以了,所以我们使用 堆 维护每个集合 最小的最大右端点 ,只要当前左端点可以大于 最小的最大右端点 所在组,就说明可以加入这个组。加入后用它的右端点更新这个组的最大右端点。
也就是用堆来维护每个组的最大右端点,当前左端点比堆顶大,就用它替换堆顶,代表更新了这个组的最大右端点。
n = int(input()) | |
nums = [] | |
for _ in range(n): | |
a, b = list(map(int, input().split())) | |
nums.append((a, b)) | |
nums.sort(key=lambda x: x[0]) | |
res = [] | |
import heapq | |
for l, r in nums: | |
if not res or res[0] >= l: | |
heapq.heappush(res, r) | |
else: | |
heapq.heapreplace(res, r) | |
print(len(res)) |
# 问题 5:AcWing 104. 货仓选址
# 题目描述
在一条数轴上有 N 家商店,它们的坐标分别为 A1∼AN。
现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。
为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
# 题目分析
简单理解题意。一个数轴上有若干数表示商店坐标,任意选择一个数表示货仓(可以与商店在同一坐标,也可以不同),该数到其他数的 距离和 最小。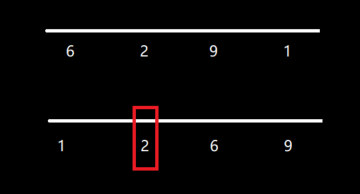
在数轴 [6, 2, 9, 1] 中选择出 2 ,它到其他三个数的 距离和 是 12 ,也就是 距离和 最小的(选 1 距离和是 14 ,选 6 距离和是 12 ,选 9 距离和是 18 )。
本题的贪心思路是将数轴按照从小大到大排序,找出中位数即可。
# 贪心证明
假设当前数轴上只有 a、b 两个商店,那么货仓 x 的位置只有三处, a、b 左面, a、b 右面, a、b 中间。那么 x 设置在哪里可以让距离和最短呢?很明显是中间。
也就是两个数的情况,一定有 绝对值不等式: |x-a| + |x-b| >= |b-a| ,而等于的情况就是当 x 在 a,b 中间。
上述情况是数轴上只有两个数,那么当数轴上的数扩展到 n 个的时候呢?我们可以分组来看。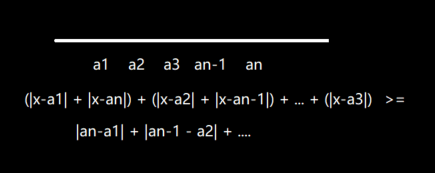
如果我们想让组 a1, an 取到最小值,那就取他们的 中间 ;想让 a2, an-1 取到最小值,也要取他们的 中间 ,以此类推。并且我们发现当数轴上有奇数个数的时候,他们的中间就是中位数,当数轴上有偶数个数的时候,他们的中间是最中间区间内的任意数
# Code
n = int(input()) | |
nums = list(map(int, input().split())) | |
nums.sort() | |
res = 0 | |
mid = nums[n // 2] | |
for i in range(n): | |
res += abs(mid - nums[i]) | |
print(res) |
# 问题 6:AcWing 125. 耍杂技的牛
# 题目描述
农民约翰的 N 头奶牛(编号为 1..N)计划逃跑并加入马戏团,为此它们决定练习表演杂技。
奶牛们不是非常有创意,只提出了一个杂技表演:
叠罗汉,表演时,奶牛们站在彼此的身上,形成一个高高的垂直堆叠。
奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。
这 N 头奶牛中的每一头都有着自己的重量 Wi 以及自己的强壮程度 Si。
一头牛支撑不住的可能性取决于它头上所有牛的总重量(不包括它自己)减去它的身体强壮程度的值,现在称该数值为风险值,风险值越大,这只牛撑不住的可能性越高。
您的任务是确定奶牛的排序,使得所有奶牛的风险值中的最大值尽可能的小。
# 题目分析
首先明确题意。一些奶牛玩叠罗汉的游戏,每个奶牛有两个属性:1. 自己的重量 wi;2. 所能承载的重量 si。以及一个风险值的属性,风险值的计算方式是自己的承载量减去身上所有奶牛的重量。最后要求 风险值的最大值,尽可能的小 。
本题的贪心思路是按照 wi+si 排序,然后计算出每头牛的风险值找出最小的就是结果。
# 贪心证明
首先从题意中,我们可以知道从前往后扫描,当前牛的风险值一定不会被它前面所有牛的顺序影响,那么我们只要关注它和它下一个牛的相对位置即可。
要证明上面很简单,影响风险值的是当前牛前面所有牛的重量之和,因此与前面所有牛的顺序无关。
【我们现在想比较一下,当前牛和下一个牛交换后的影响。】
假设, 牛i 的风险值是: w[1] + w[2] + ... + w[i-1] - s[i] ,可以记作:。
而 牛i+1 的风险值是: w[1] + w[2] + ... + w[i] - s[i+1] ,可以记作:。
【现在,我们让两头牛的顺序交换一下,那么当前牛的下标是 i+1 ,而下一个牛的下标是 i 。】
此时, 牛i 的风险值是: w[1] + w[2] + ... + w[i-1] + w[i+1] - s[i] ,可以记作:。
此时, 牛i+1 的风险值是: w[1] + w[2] + ... + w[i-1] - s[i+1] ,可以记作:。
可以看到上面四个式子中全部包含,因此将该公式全部去掉,可以得到以下表格:
| 牛 | i | i+1 |
|---|---|---|
| 交换前 | . | |
| 交换后 | . |
由于,此处 w 和 s 都是正数,所以一定有 和。
因此,比较 与 即可。
如果是,那么可以直接推出,即当交换前风险值大于等于交换后,因此交换后更优。
如果是,那么可以直接推出,即交换前风险值小于交换后,因此交换前更优。
那么我们就把所有的牛按照 wi+si 从小到大排序,然后计算风险值,找出其中最大的,就是我们要的尽可能小的最大风险值。
# Code
n = int(input()) | |
nums = [] | |
for _ in range(n): | |
w, s = list(map(int, input().split())) | |
nums.append((w, s)) | |
nums.sort(key=lambda x: x[0] + x[1]) | |
res = float('-inf') | |
totle = 0 | |
for i in range(n): | |
res = max(res, totle - nums[i][1]) | |
totle += nums[i][0] | |
print(res) |
# 总结
从上面题目的例子中可以看出来,贪心问题一般是比较困难的题目,因为它并不是一步一步推导结果的,而是先凭借经验,随便猜一个做法,然后一步一步去证明该做法的正确性。
END