# 字典树
字典树:高效的 存储 和 查找 字符串集合 的基础数据结构,又叫 Trie 树、前缀树等。
# 字典树的结构
假设现在有一个问题是这样的:
给出一个单词序列,再给出一个单词,查找该单词 是否 在序列中出现过。
例如:给出单词序列为:
[apple, app, able, abc]给出的单词为
and,那么结果应该是False;给出单词为able,那么结果应该是True;
# 暴力思路分析
暴力思路很简单,我们只需要先遍历单词序列中的每个单词,对于每个单词,都判断一下 是否与给出单词匹配。
当然,这其中还可以加入判断单词长度是否一致等优化。但是总体而言,时间复杂度还是来到了 O (n),既每次都需要遍历单词序列中的所有单词。
# 字典树的思路
我们可以把单词序列建立成一种类似字典的树形结构,既如图所示:
我们按照以下的规则建立字典树:
- 首先,我们要建立一个根节点 root;
- 遍历每个单词,遍历该单词的每个字母;
- 我们从 root 节点开始判断,下一个字母 在不在 root 的子节点上,没在的话 就把 下一个字母 在子节点上 创建出来;
- 随着循环的进行,下一个字母 变成 新的 root 节点,下一个字母的下一个字母 变成 新的 "下一个字母"
- 随着循环的进行,操作 3 和 4 会不断重复,直到一个单词遍历完毕之后,我们在它的后面记录一下 到此为止 是一个单词(图中用绿色井号表示);
- 当整个单词序列都遍历完之后,这颗字典树就建立完整;
举个例子比如,单词 apple:
- 第一个 "下一个字母" 是 a,那么 root 的子节点上没有 a,我们把它创建出来;
- a 变成 root;下一个字母变成 p,那么 root 的子节点上还是没有,我们继续创建出来 p;
- p 变成 root,p 的下一个字母还是 p,那么 root 的节点仍然没有,我们继续创建;
- 以此类推。。。。。;
建立字典树之后,我们就可以快速的沿着字典树来查找一个单词,比如对于 and :
我们从根节点 root 开始查找;
判断
下一个字母a是不是root的子节点呢?这会有两种情况:- 是子节点,那么继续向下找;
- 不是子节点,说明当前单词不存在,查找结束,返回
False;
a 变成新的根节点,n 变成下一个字母,重复步骤 2,在步骤 2 结束了本次查找,
and不存在;假如可以顺利找到最后一个字母 d,那么,我们就判断
d上面是否有绿色井号标记,如果有说明单词存在,反之,单词仍然不存在;
# 代码模板
参照下面的题目 [835. Trie 字符串统计] 的代码部分。
# 835. Trie 字符串统计
维护一个字符串集合,支持两种操作:
I x 向集合中插入一个字符串 x;
Q x 询问一个字符串在集合中出现了多少次。
共有 N 个操作,输入的字符串总长度不超过 105,字符串仅包含小写英文字母。输入格式
第一行包含整数 N,表示操作数。
接下来 N 行,每行包含一个操作指令,指令为 I x 或 Q x 中的一种。
输出格式
对于每个询问指令 Q x,都要输出一个整数作为结果,表示 x 在集合中出现的次数。
每个结果占一行。
数据范围
1≤N≤2∗104输入样例
5 I abc Q abc Q ab I ab Q ab输出样例
1 0 1
# 题目描述
给出一个字符串集合,给出两种操作:
- 向集合中插入一个字符串 x;
- 询问一个字符串,在字符串集合中出现了多少次,注意本题要求的是出现次数,而非是否出现;
# 题目分析
我们以本题作为模板题,来看一下如何实际的使用字典树。
# Code
在实现上,我们使用二维数组来实现,其中有几个关键的变量需要充分理解:
idx:我们使用 idx 来表示每个节点的编号,要注意 idx 是无限增长的,我们不需要关注它的值到底是多少,只要知道 idx 标志着每个节点的唯一编号,比如,根节点的唯一编号,我们可以设置为 0。(但是额外注意 0 不只表示根节点,它还表示空值,比如son[0][a]==0表示a不是根节点 root 的子节点)。son[N][26]: son 数组是个二维数组。顾名思义,它存储了每个节点编号的儿子节点的编号。比如,根节点 root 下面有一个字母a,字母a的节点编号是 7,则表示为son[0][a] = 7;请注意编号为7的节点,虽然是a,但是这个a一定是节点编号为0下的a! 如果是其他节点编号下的a的编号则不会是7。进一步的,如果 节点编号
0下面的a的下面 还有一个字母p,那么我们需要让a的节点编号变成新的根节点 root,并且让 p 成为 root 的子节点,给 root 下的 p 一个编号 idx,代码为root = son[root][a], son[root][p] = ++idx。cnt:在本题中,我们需要统计每个单词的数量,所以cnt[root]表示以 节点编号为 root 为结尾的单词 的数量。
#include <iostream> | |
using namespace std; | |
const int N = 100010; // 节点数量 | |
int son[N][26]; | |
int cnt[N], idx; | |
char str[N]; | |
// 插入一个字符串 | |
void insert(char str[]) { | |
int root = 0; // 初始的 root 节点的编号是 0 | |
for (int i = 0; str[i]; i ++ ) { | |
int u = str[i] - 'a'; // 下一个字母 | |
// 下一个字母 在根节点中如果不存在 则创建出来 | |
// 下一个字母的编号是 ++idx | |
if (!son[root][u]) son[root][u] = ++ idx; | |
root = son[root][u]; // 下一个字母的编号变成新的 root 节点 | |
} | |
cnt[root] ++ ; // 一个单词插入完毕 且 以 root 结尾 | |
} | |
// 查找一个字符串 | |
int query(char str[]) { | |
int root = 0; // 初始的 root 节点的编号是 0 | |
for (int i = 0; str[i]; i ++ ) { | |
int u = str[i] - 'a'; // 下一个字母 | |
// 如果下一个字母在 root 的子节点上不存在 那么直接返回 0 | |
if (!son[root][u]) return 0; | |
root = son[root][u]; // 下一个字母的编号变成新的 root 节点 | |
} | |
// 当该单词找到之后, 返回它的数量 | |
return cnt[root]; | |
} | |
int main() { | |
int n; | |
cin >> n; | |
for (int i = 0; i < n; i ++ ) { | |
char op[2]; | |
scanf("%s%s", op, str); | |
if (op[0] == 'I') insert(str); | |
else printf("%d\n", query(str)); | |
} | |
return 0; | |
} |
# AcWing 143. 最大异或对
在给定的 N 个整数 A1,A2……AN 中选出两个进行 xor(异或)运算,得到的结果最大是多少?
输入格式
第一行输入一个整数 N。
第二行输入 N 个整数 A1~AN。
输出格式
输出一个整数表示答案。
数据范围
1≤N≤10^5, 0≤Ai<2^31输入样例
3 1 2 3输出样例
3
# 题目描述
给定 N 个整数,从 A [1~n],选出所有整数中的两个进行异或运算,得到的结果,最大会是多少?
首先,明确一下异或运算,比较两个数的二进制位,相同为 0,不同为 1。例如:
然后看下示例。示例中给出的三个数,两两异或,则有下面三种组合方式:
- 1^2==3;
- 1^3==2;
- 2^3==1;
所以,示例中的数字两两异或的最大值是 3。
# 题目分析
那么,这题和字典树有什么关系呢?我们还是得从暴力的做法开始摸索。
简单的暴力做法,双重循环,维护最值。
for (int i = 0; i < n; i ++ ) | |
for (int j = 0; j < n; j ++ ) | |
res = max(res, a[i] ^ a[j]) |
那么,因为双重循环的原因,暴力做法的时间复杂度是 O (n^2) 的,而 n 的范围是,一定会超时的。所以我们考虑一下优化。
在暴力做法里,我们的思路是:
- 枚举出每一个
a[i]; - 然后通过
a[i]和 所有的a[j]运算,找出最大的。
很明显,枚举 a[i] 是没有什么优化空间的,但是第二步的一个 a [i] 异或 上哪个数的值最大是可以优化的。
我们考虑一个二进制数 1100101....10 ,假设该数总共 31 位,为了方便记,我们就称该数为数字 A。那么我们想让这个数 异或运算之后 最小,应该异或上一个什么样的数呢?为了方便记,我们就称 进行异或运算的这个数,为数字 B。
我们要如何考虑数字 B 的组成呢?
首先考虑第一位(最高位),因为数字 A 的第一位是
1,所以我们期待数字 B 的第一位是0,这样 A 异或 B 的结果才能是1;数字 A 的第二位是
1,所以,我们期待数字 B 的第二位是0;数字 A 的第三位是
0,所以,我们期待数字 B 的第三位是1;数字 A 的第四位是
0,所以,我们期待数字 B 的第四位是1;数字 A 的第二位是
1,所以,我们期待数字 B 的第二位是0;
以此类推,我们可以发现,我们对数字 B 的期待是,与数字 A 同位置上的数,相反的数,如果没有相反的数,我们再选择相同的数。
所以,我们可以把对 B 的这种期待,用树形结构表示出来。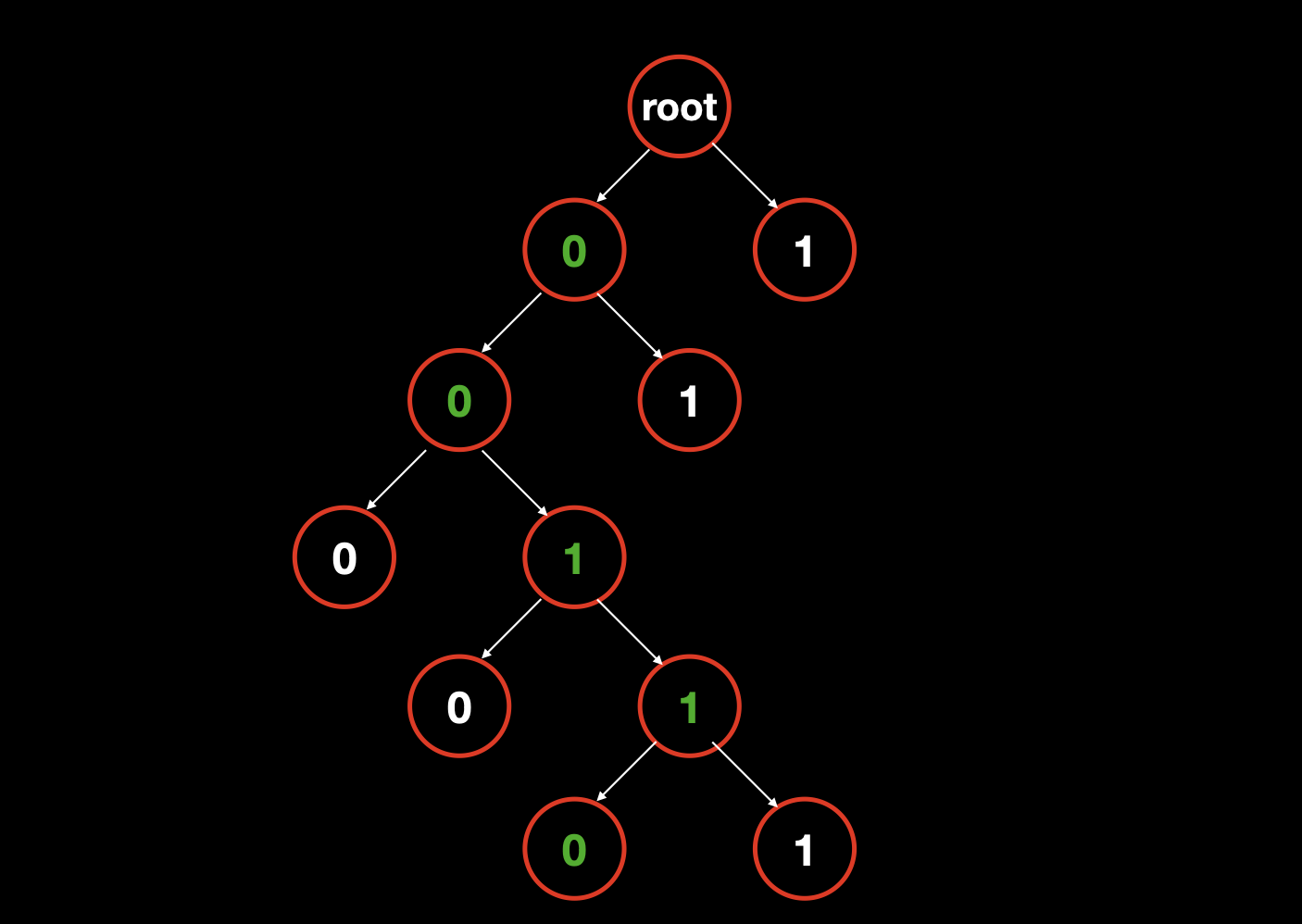
诶?我们神奇的发现,这个树形结构和我们今天所学习的字典树竟然高度相似。这就启发我们可以提前 按照 01 的分支结构,把 给定序列 的所有数 的二进制 装到字典树里。
这样做的好处是,当我们想要找数字 B 的时候,可以沿着我们所期待 01 数字的进行搜索,而搜索次数则是树的高度,这样我们就把时间复杂度优化成 O (nlogn)。
举个例子,比如说对于数列 [2,3,4,5,6] ,把他们全部转换成二进制就是 [010, 011, 100, 101, 110] ,建立 01 字典树就是如下图所示的结果。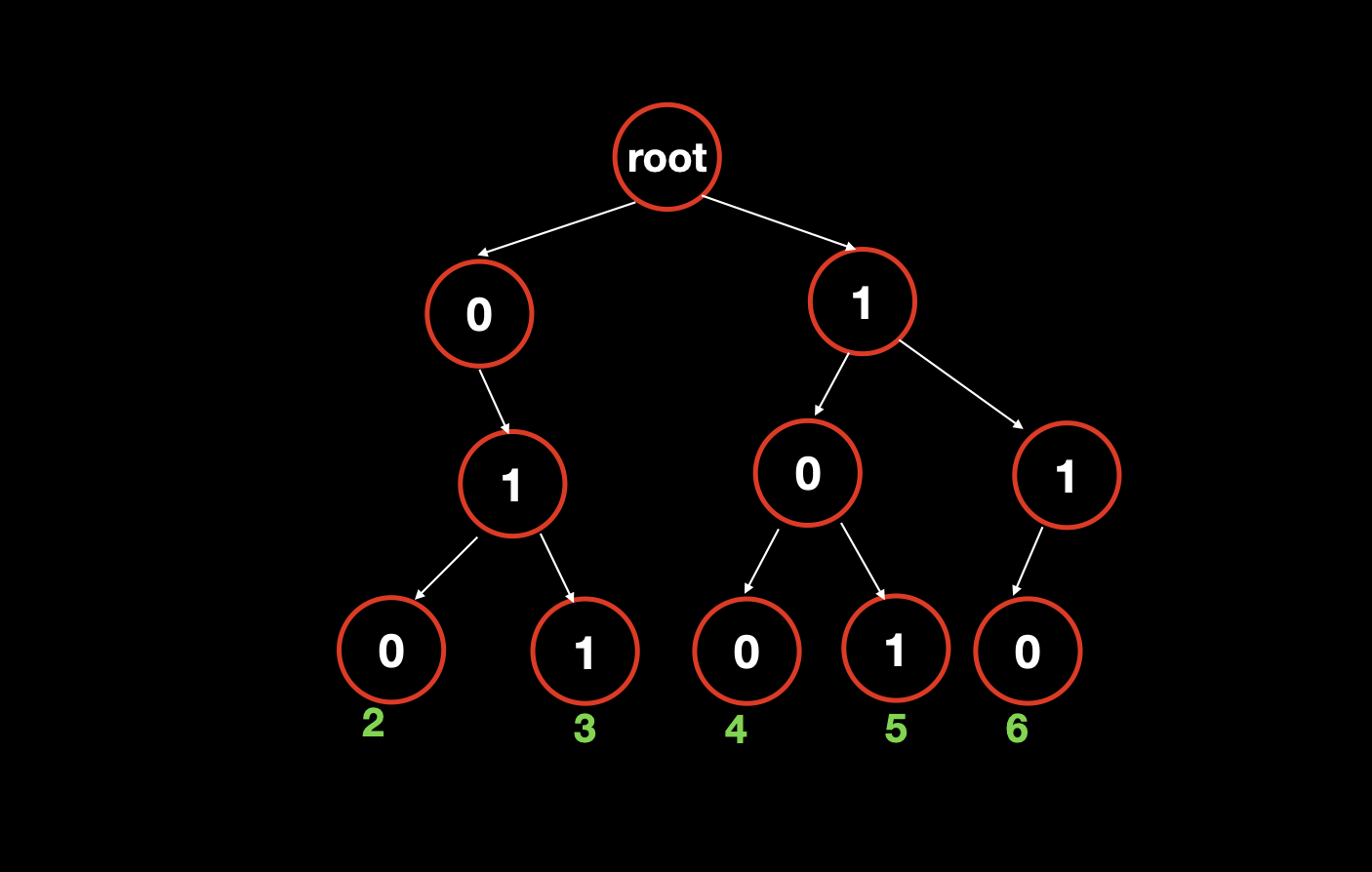
当我们要找 010 的异或最大值时,我们发现是 101 ,也就是数字 5,它俩的异或结果是 7 ;我们要找 011 的异或最大值时,我们发现是 100 ,也就是数字 4,它俩的异或结果也是 7;以此类推,我们就找到了最终的最大值。
# Code
因为本题的实现上,本质是对二进制位的操作,所以我们必须先熟悉本题中的基本的操作。
拉出来二进制的第 i 位是 0 还是 1,可以用
x >> i & 1。左移 i 位,就是把第 i 位移动到最后,与操作两位都为 1 则是 1,否则是 0,因此与 1 的作用就是,最后一位如果是 1,那么结果就是 1,如果是 0,结果则是 0。
求结果的时候,要通过二进制位还原出十进制位。
假设,当前二进制位是第 i 位,则res += 1 << i即可,就是加上了 ,这里运用了二进制转十进制公式。
#include <iostream> | |
using namespace std; | |
const int N = 100010, M = 3000010; | |
int n; | |
int son[M][2], idx; | |
int a[N]; | |
int insert(int x) { | |
int root = 0; | |
for (int i = 30; ~i; i -- ) { | |
int t = x >> i & 1; | |
if (!son[root][t]) son[root][t] = ++ idx; | |
root = son[root][t]; | |
} | |
} | |
int query(int x) { | |
int root = 0, res = 0; | |
for (int i = 30; ~i; i -- ) { | |
int t = x >> i & 1; | |
// 注意这里判断!t(1 变 0 0 变 1)在不在树中 在 则选择!t | |
if (son[root][!t]) { | |
root = son[root][!t]; | |
res += 1 << i; // 二进制计算十进制 | |
// 注意最终答案 是两个数字做 异或操作 的结果 | |
// 二进制位 相异的数 不在树中 只能选择相同的数 | |
// 而相同的数 异或 为 0 | |
// 0 不会为最终答案 提供有效数字 | |
} else root = son[root][t]; | |
} | |
return res; | |
} | |
int main() { | |
cin >> n; | |
for (int i = 0; i < n; i ++ ) { | |
cin >> a[i]; | |
insert(a[i]); | |
} | |
int res = 0; | |
for (int i = 0; i < n; i ++ ) res = max(query(a[i]), res); | |
printf("%d\n", res); | |
return 0; | |
} |
END