# 前置知识

图论基础之匈牙利算法求二分图的最大匹配

# 最小点覆盖问题

最小点覆盖：给出一个图，从中选出最少的点，使得每一条边的两个点里面至少有一个点是被选出来的。
在二分图中，最小点覆盖有一个结论：最小点覆盖数量 == 最大匹配数量。

# 结论证明（可略过）

若想证明一个相等的结论，比如：A==B，我们可以先证明 A>=B，再证明 A<=B，这样就能推出来 A==B，然而如果我们想求出来 A 最小，那么其实只需要证明 A>=B 且 A==B，因为一定是取到等号的时候 A 才最小，所以我们就有本结论以下的证明方式：

最小点覆盖 >= 最大匹配数量
这点可以从定义上来证明，最小点覆盖最终的目标是使得所有的边中任意一条边都有一个点被选出来，而最大匹配数量是从所有的边中选择出来匹配的，那么选择出来的一定是被包含在所有边中，所以有最小点覆盖 >= 最大匹配数量。
最小点覆盖 == 最大匹配数量
这点可以使用构造的方式来证明。假设，我们能构造出来一个方案，恰好选择 m （最大匹配数为 m ）条边，使得 m 条边能够覆盖到所有的边，因此，根据定义，m 就是最小点覆盖，进而推出等号成立。
如何构造呢？我们可以分为两步:
1. 求最大匹配；
2. 从左边每个非匹配点开始做增广。

# 求最大匹配

使用匈牙利算法，先求一次最大匹配的数量。其中白色线表示可匹配的边，红色表示匹配成功的边。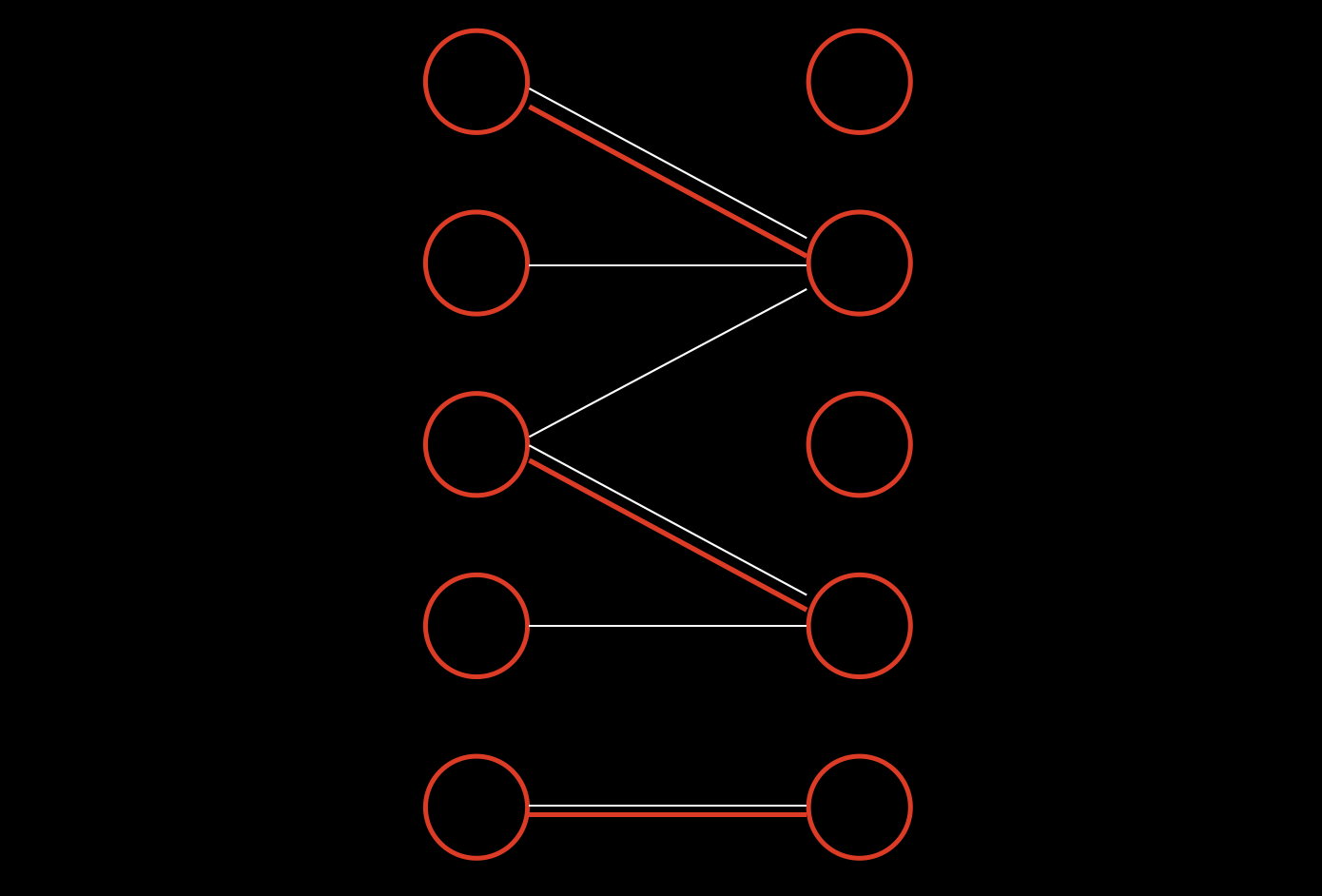

# 从左边每个非匹配点开始做增广

从左边的每个非匹配点出发，做一遍增广，在过程中标记所有经过的点（这个增广操作是一定会失败的，因为我们上一步已经求了一遍匈牙利算法，完成了所有可以成功的增广操作）。

最大匹配里的增广：对于这个概念还不熟悉的同学，请复习前置文章匈牙利算法，重点理解算法过程中的步骤 3 和 4。

首先左边 2 号点和 4 号点是非匹配点。

增广步骤为，先从左 2 号点出发到达右 2 号点，再从右 2 号点到达左 1 号点，因此将这三个点用绿色圈标记起来；再从左 4 号点出发到达右 4 号点，然后从右 4 号点到达左 3 号点，因此再将这三个点用绿色圈标记出来。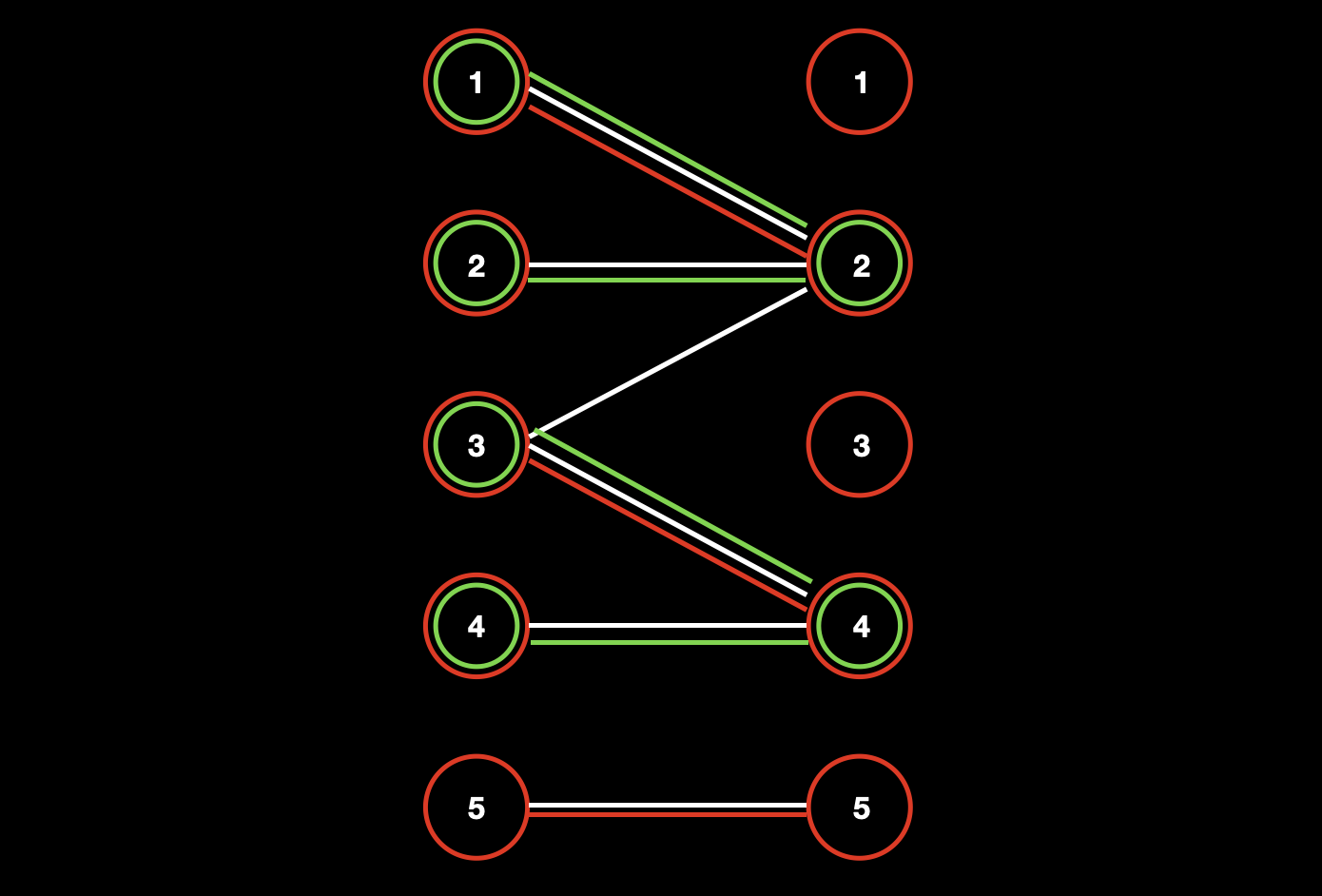

左边所有未被标记的点 和 右边所有被标记的点 数量加起来就是一种最小点覆盖的方案（从图中可以直观的看到最小点覆盖是 3，因为右边 1 号点和 3 号点是孤立点，没有连接边）。

# 证明该方案符合最大匹配数量

那么，如何证明这种方案就是最大匹配数量 m 呢？

根据增广规则，左部所有非匹配点，一定全部被标记（因为他们都是起点）。
右边所有的非匹配点，一定没有被标记。因为如果右边的非匹配点被标记，那么就是一条新的匹配路径，但是，要知道我们在证明的最初已经做了一遍匈牙利算法，从而求出来了所有的匹配边，因此不可能再存在新的匹配边。
对于所有的匹配边，边的两点必然都被标记或者都没有被标记。
注意，还有一种隐含规则，不可能存在左右两个连接点，既没被标记，也没有匹配，因为这种情况下，这两个点一定是可以匹配的，但是我们在第一步求最大匹配的时候，已经将所有匹配都找出来了。

综合上述三条性质，我们发现左边所有未被标记的点一定是匹配点（因为左边的非匹配点全部被标记到了）；右边所有被标记的点一定是匹配点（因为右边没被标记的点，一定是非匹配点）。

所以，我们按照上述规则选择的话，对于任意一条匹配边，我们必然都只选择了一个点。如果匹配边的两点被标记了，我们选择的就是右边，如果没被标记，我们选择的就是左边的点。

并且，我们所有选择的点，必然都是匹配边上的点，这就说明，我们选择出来的所有匹配点的数量就是最大匹配 (边) 的数量。

# 证明该方案是最小覆盖数量

我们再来看不在匹配中的边，可以分为两种情况：

左边的非匹配点连接到右边的匹配点（与上节的第三条矛盾）；
已知左边的非匹配点是被标记的，根据增广标记的规则，被该点直接连接的右面点，一定也是被标记的，而右面所有被标记的点都会被我们选择出来。所有这种情况下的非匹配边的右点一定被选择。
左边的匹配点连接到右边的非匹配点（与上节的第三条矛盾）；
左边的匹配点如果指向了右边的非匹配点，那么左边的匹配点一定不会被标记，因为左匹配点在做增广时不是起点，如果它被标记了，一定是从右面过来的，那么从右面过来的那个点一定也被标记了，可是在上节，我们知道右面的非匹配点是不会被标记的。

所以，我们就用同样的方法（左边所有未被标记的点 和 右边所有被标记的点 数量加起来）构成了一种最小点覆盖的方案，该方案中如果边是匹配的，我们选择的点就是右面的，如果边是不匹配的，我们选择的点就是左面的，因此满足所有的边都取一个点的最小点覆盖定义。

因此，这种方法既是最小点覆盖方案，又是最大匹配数量的方案，因此就可以推出最小点覆盖 == 最大匹配数量。

# AcWing 376. 机器任务

有两台机器 A，B 以及 K 个任务。
机器 A 有 N 种不同的模式（模式 0∼N−1），机器 B 有 M 种不同的模式（模式 0∼M−1）。
两台机器最开始都处于模式 0。
每个任务既可以在 A 上执行，也可以在 B 上执行。
对于每个任务 i，给定两个整数 a [i] 和 b [i]，表示如果该任务在 A 上执行，需要设置模式为 a [i]，如果在 B 上执行，需要模式为 b [i]。
任务可以以任意顺序被执行，但每台机器转换一次模式就要重启一次。
求怎样分配任务并合理安排顺序，能使机器重启次数最少。
输入格式
输入包含多组测试数据。
每组数据第一行包含三个整数 N,M,K。
接下来 K 行，每行三个整数 i,a [i] 和 b [i]，i 为任务编号，从 0 开始。
当输入一行为 0 时，表示输入终止。
输出格式
每组数据输出一个整数，表示所需的机器最少重启次数，每个结果占一行。
数据范围
N,M<100,K<1000
0≤ a[i] < N
0≤ b[i] < M
输入样例
5 5 10
0 1 1
1 1 2
2 1 3
3 1 4
4 2 1
5 2 2
6 2 3
7 2 4
8 3 3
9 4 3
0
输出样例
3

# 题目描述

有两台机器 A 和 B，并且给出 K 个任务，再给出两个数组 a [i] 和 b [i] 表示两个机器执行第 i 个任务需要使用的模式，每转换一次模式机器就要重启动一次，问 执行完 K 个任务最少需要重启多少次机器。

# 题目分析

首先，题目中给出两个机器都从模式 0 开始，并且任务不必按照顺序执行，所以我们可以先把所有使用模式 0 执行的任务先全部完成（避免切换模式），所以剩下的任务都是大于 0 的。

因此问题就变成了在 N+M-2 （其中 N 和 M 是两种机器的模式数量）种模式中，最少选出多少个模式可以把所有剩余的任务完成。

如果我们把 a [i] 和 b [i] 看成 a [i] 连向 b [i] 的一条有向边，那么完成任务 i 就相当于是在这条边上选择出一个点。如此，我们就把问题转换成了，在这个二分图中选择出最少的点，把所有的边覆盖到，也就是最小点覆盖问题，那么二分图中的最小点覆盖问题就等价于最大匹配数量，因此我们直接使用匈牙利算法求出最大匹配数量就是本题的答案。

# Code

	#include <iostream>
	#include <cstring>

	using namespace std;

	const int N = 110, K = 1010;
	bool g[N][N], st[N];
	int match[N];
	int n, m, k;

	// 匈牙利算法模板
	int find(int u) {
	// 遍历集合 b 用来找与 u 匹配的
	for (int i = 1; i < m; i ++ ) {
	// 如果有边并且 b 中的点没有被使用则可以匹配
	if (g[u][i] and !st[i]) {
	st[i] = true;
	int t = match[i];
	// 如果点 i 没有匹配对象或者可以给它找到其他对象
	// 那么就把当前点 u 匹配给它
	// 所以当前点 u 就可以找到一个匹配对象
	if (t == -1 or find(t)) {
	match[i] = u;
	return true;
	}
	}
	}
	return false;
	}

	int main() {
	while (cin >> n, n) {
	cin >> m >> k;
	// 多组数据千万别忘记初始化
	memset(g, 0, sizeof g);
	memset(match, -1, sizeof match);
	while (k -- ) {
	int t, a, b;
	cin >> t >> a >> b;
	if (!a or !b) continue;
	g[a][b] = true; //a [i] -> b [i] 之间有一条边
	}
	// 匈牙利算法模板
	int res = 0;
	// 遍历集合 a 对于每个点都进行匹配
	for (int i = 1; i < n; i ++ ) {
	memset(st, 0, sizeof st);
	if (find(i)) res ++ ;
	}
	cout << res << endl;
	}
	return 0;
	}

经典必会 AcWing算法提高课匈牙利算法二分图的最小覆盖问题