# AcWing 849. Dijkstra 求最短路 I(图论中的基础最短路问题)
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。如果路径不存在,则输出 −1。
数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过 10000。输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
# 题目描述
如题,给定一个 n 个点和 m 条边的有向图,所有边权均为正。求 1 号点到 n 号点的最短距离,如果没办法从 1 号点到 n 号点,则输出 - 1。
# dijkstra 思路
如题目标题所写,本题就是 Dijkstra 求最短路的一个标准应用场景。即,求 n 个点 m 条边组成的图中,某个点到其他点的最短距离且边权为正。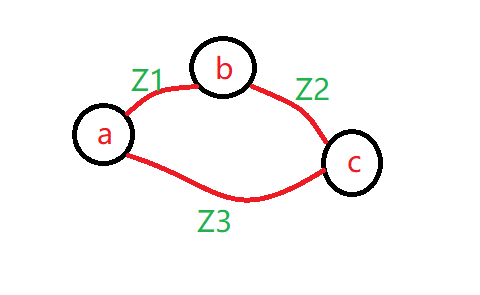
Dijkstra 算法本身并不难理解,较麻烦的地方在于实现上,所以记住一个好用的模板还是很重要的。Dijkstra 本质是贪心原理:
在上图中,我们如果想知道【从 1 号点到其他点的最短距离】。
首先我们从 a 点出发,可以经过 z1 距离到 b 号点,经过 z3 距离到 c 号点。因此,目前我们可以得出初步结论 a 点到 b 点的距离是 z1,a 到 c 的距离是 z3;
由于 a 与 b 中没有其他点,所以 z1 一定就是 a 到 b 的最短距离;
我们又注意到 a 到 c 点的距离为 z3,但是 z3 一定是 a 到 c 的最短距离吗?
不一定的,因为 a 到 c 还有另外一条路,即,a 到 b 再到 c,那么我们如何判断两条路径的哪条更短一些呢?
因为我们已经知道了 z1 是 a 到 b 的最短距离,那么我们直接用 z1 加上 z2 就是 a 到 b 再到 c 的距离,如果该距离比 a 直接到 c 更小,那么就可以用 a 到 b 的最小距离 z1 加上 z2 的结果,来更新 a 到 c 的最小距离;
如此,我们就求出了 1 号点 a 到其他两个点的最短距离分别是多少;
# Code
# 朴素版
根据上面的分析,看一下我们在代码中需要如何进行操作。
首先必须有一个数据结构来记录距离,我们选用数组,因为数组的下标就可以代表当前的点编号,而其对应的值就是它到 1 号点的距离。用 dist 表示;
我们必须有一个数据结构来记录已经确定最短路径的点,因为分析中我们提到只有当 z1 为最短路径的时候,才可以用它加上 z2 来更新 a 到 c。所以我们有必要记录已经确定的点。那么因为最短路径有且只有一个,所以我们用集合 set 来存储已经确定的最短距离的点。用 st 表示;
必须有一个数据结构来存储给出的信息,即点 a 到 b 的距离 z1。我们直接使用邻接矩阵来存储,即矩阵第一维表示出发点,第二维表示到达点,其对应的值表示边长的距离,也就是边的权重。例如:g [a][b]=z1;
初始化 dist,第一个点为 0,其他所有点为正无穷;
循环所有的点(1~n)。找到不在 st 中的距离最近的点 t,放到 st 中,用 t 更新其他点的距离。更新条件为如果 t 到 x 的距离加上 t 到 1 号点的距离小于 x 直接到 1 号点的距离,则可以更新。当循环结束后,我们一定可以确定某一个点的最短距离(每次确定的都是不在 st 中且与 1 号点最近的点,贪心原理,证明过程不在此赘述);
把过程 5 再循环 n 遍就求出了 n 个点到 1 号点的最短距离。
# Dijkstra 算法 | |
n, m = map(int, input().split()) | |
# 本题中 n 的范围是 500 m 是 10^5 大于 n^2 所以是稠密图 要用邻接矩阵 用 g 表示 | |
# 其中为什么要 n+1?这是让下标都从 1 开始,方便处理且符合人类的思考逻辑 | |
g = [[float('inf')] * (n + 1) for _ in range(n + 1)] | |
# dist 分析中已经提过,用来记录 1 号点到 i 的距离 | |
dist = [float('inf')] * (n + 1) | |
# st 表示每个点数是否已经是确定的。 | |
st = set() | |
# 初始化邻接矩阵。 | |
for _ in range(m): | |
x, y, z = map(int, input().split()) | |
# 因为题目中说可能有重边,也就是一个点到另外一个点可能有多个边 | |
# 所以我们只保存最短的那条边。 | |
g[x][y] = min(g[x][y], z) | |
# 初始化第一个点为 0,就是它到自己的距离。 | |
dist[1] = 0 | |
# 注意要循环 n 遍,每遍都会确认一个点, | |
# 确认的点为不在 st 中,并且与 1 号点最近的点 | |
for _ in range(n): | |
# 初始化 t | |
t = -1 | |
for i in range(1, n + 1): | |
# 如果 i 不是已经确定的点, | |
# 并且是未赋值的(也就是等于初值 - 1)或者 dist 中 t 大于 i 说明 i 更短 | |
# 所以用 i 更新 t, 并且最后把 t 加到集合中 | |
if i not in st and (t == -1 or dist[i] < dist[t]): | |
t = i | |
st.add(t) | |
# 用 t 更新其他点的距离 | |
for j in range(1, n + 1): | |
# 这里 j 直接到 1 号点,或者 j 先到 t 再到 1 号点,那个最小就用那个。 | |
dist[j] = min(dist[j], dist[t] + g[t][j]) | |
# 最后求出 1 到 n 的最短距离就行了。 | |
print(-1 if dist[-1] == float('inf') else dist[-1]) |
比较明显,时间复杂度是
# 堆优化
我们很容易发现上面的算法最大时间复杂度是 O (n^2) 的。又可以发现最耗时的其实是在找不在 st 中并且当前距离 1 号点最小的数 t 的这一步。那我们要在一堆数中找出最小的数可不可以借用什么现成的数据结构呢?没错,那就是堆。代码整体思路没有变化。
优化后,时间复杂度是。
from collections import defaultdict | |
from heapq import heappush, heappop | |
n, m = map(int, input().split()) | |
# 点的数量与边的数量差不多 所以是稀疏图 用邻接表存储 | |
g = defaultdict(lambda: defaultdict(lambda: float('inf'))) | |
for _ in range(m): | |
x, y, z = map(int, input().split()) | |
g[x][y] = min(g[x][y], z) | |
dist = [float('inf')] * (n + 1) | |
dist[1] = 0 | |
heap = [] | |
# 需要把当前节点到 1 号点的距离,和当前节点编号都入堆 | |
heappush(heap, (0, 1)) | |
st = set() | |
while heap: | |
# 弹出当前最小的点 | |
d, node = heappop(heap) | |
# 如果当前点再 st,则略过即可 | |
if node in st: | |
continue | |
st.add(node) | |
# 枚举当前点可以到达的点 p | |
for t in g[node]: | |
# 用 t 更新其他距离 | |
if dist[t] > d + g[node][t]: | |
dist[t] = d + g[node][t] | |
heappush(heap, (dist[t], t)) | |
print(dist[-1] if dist[-1] != float('inf') else -1) |
# 时间复杂度
实际应用一下我们的模板。
# LeetCode 743. 网络延迟时间
# 题目描述
不再过多赘述题意,点击题目链接可以跳转到原题。读完题立刻就能发现,这道题也近乎是一道最短路问题的纯模板题。
# 题目分析
和我们上面分析的模板唯一不同的地方就在于【从某个节点 k 发出一个信号,需要多久才可以使所有点都收到信号】,这说明我们要求出 k 到所有点的最短距离,那么这些距离中最大的那个就是结果。
# Code
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int: | |
g = [[float('inf')] * (n + 1) for _ in range(n + 1)] | |
for x, y, z in times: | |
g[x][y] = z | |
dist = [float('inf')] * (n + 1) | |
# 注意!!!唯有此处不同,从 k 点出发,那么初始化 k 到它自己的距离是 0 | |
dist[k] = 0 | |
st = set() | |
for _ in range(n): | |
t = -1 | |
for i in range(1, n + 1): | |
if i not in st and (t == -1 or dist[t] > dist[i]): | |
t = i | |
st.add(t) | |
for j in range(1, n + 1): | |
dist[j] = min(dist[j], dist[t] + g[t][j]) | |
res = max(dist[1:]) | |
return res if res < float('inf') else -1 |