前置知识:图论基础之 Dijkstra 求最短路
# AcWing 853. 有边数限制的最短路
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出 impossible。
注意:图中可能 存在负权回路 。
输入格式
第一行包含三个整数 n,m,k。接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
点的编号为 1∼n。
输出格式
输出一个整数,表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。如果不存在满足条件的路径,则输出 impossible。
数据范围
1≤n,k≤500, 1≤m≤10000, 1≤x,y≤n, 任意边长的绝对值不超过 10000。输入样例
3 3 1 1 2 1 2 3 1 1 3 3输出样例
3
# 题目描述
给定一个有 n 个点和 m 条边的有向图,图中可能存在重边和自环,并且存在负权边,并且存在负权回路。问题是让我们求出从 1 号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出 - 1。
# bellman-ford 思路
给出一个图,求最短路,很容易想到直接用 Dijkstra,但是这个题是否可以用呢?
我们先回顾一下 dijkstra,它的核心思路总共分为三个步骤:
先循环所有点,找到未被标识且距离源点最近的点 t;
将 t 标识起来,并且用 t 更新其他点,更新的规则是如果 t 到 x 的距离加上 t 到源点的距离小于 x 直接到源点的距离,则可以更新;
将前两步循环 n 次,就找到了 n 个点到源点的最短路径;
可以看到在第二步最关键的一步,我们使用已经找到了最小距离的点 t 去更新了其它点的最小距离,而如果存在负权边的情况下,这个更新可能就是错误的,因为在有负权边的情况下,我们找到的最小距离 dist [t] 可能就不是正确的,自然也无法更新其他点。
正确的解决方法是使用标题中提到的 bellman-ford,与 dijkstra 一样,它也是用来求最短路的,它最大的一个特点就是可以用来求出有边数限制的最短路问题。
# bellman-ford 的思路
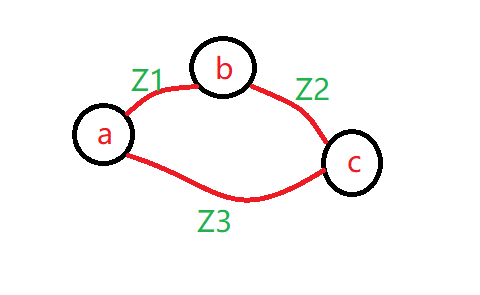
它的更新方式和 dijkstra 相差不多。
源点为 a,它到 b 的距离为 z1,b 到 c 的距离为 z2,a 到 c 的距离为 z3;我们循环其中每个点 b、c 到指向目标 a 的距离,并且用相邻点去更新(更新也叫松弛),更新的规则是:c 到 b 再到 a,也就是 z2+z1,如果比(z3)c 直接到 a 小,就用 z1+z2 更新 dist [c],这样在循环结束之后即可得到结果。
要说明的是当图中存在负权回路的时候,可能不会有最短路径,因为如果有负权回路,我们可以在回路中转很多圈,每转一圈就会使路径减小,如果回路中转无数圈则当前路径变成负无穷,那么从回路中出去之后,路径仍是负无穷。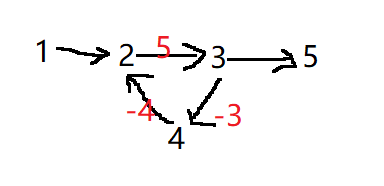
# Code
在 bellman-ford 中,每次更新会把每条边都更新一下,那么更新 n-1 次就可以更新出结果啦,如果第 n 次还可以继续更新说明图中有负环,无法得出结果。
实际操作比较简单,只需要两层循环:
循环 n 次;
每次循环都把所有的边都更新一遍;
for i in range(n): | |
for a, b, w in g[i]: | |
dist[b] = min(dist[b],back[a] + w) |
其中 back 表示上一轮更新完之后结果的备份,因为在每次循环 i 中,所有的边都会被更新中,因此需要备份,否则可能影响到相关点,发生串联效应。比如说先更新了 a,又用更新之后的 a 去更新其他点;
时间复杂度:比较明显,两层循环,所以总共为 O (n^2)。
from copy import deepcopy | |
# 读入数据 | |
n, m, k = list(map(int, input().split())) | |
g = [] | |
for _ in range(m): | |
a, b, w = list(map(int, input().split())) | |
g.append([a, b, w]) | |
# 初始化距离 | |
dist = [float('inf')] * (n + 10) | |
dist[1] = 0 | |
def bellman_ford(): | |
# 本题要求只能经过 k 条路径,因此我们遍历的路径数也是 k | |
for i in range(k): | |
# 备份结果 | |
back = deepcopy(dist) | |
for a, b, w in g: | |
# 用 b 点此时的最短距离 和 先到 a 再到 b 哪个更短 来更新 b 的最新最短距离 | |
dist[b] = min(dist[b], back[a] + w) | |
return 'impossible' if dist[n] == float('inf') else dist[n] | |
print(bellman_ford()) |
实战演练一下
# LeetCode 787. K 站中转内最便宜的航班
# 题目描述
和上面的题基本一样。
# 题目分析
从题目中可以分析出,由所有城市组成了一个图,而价格则是每个边的权重,又发现给出了条件最多经过 k 个点可知,本题应该用 bellman-ford。所以再默写一遍就可以了。
# Code
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int: | |
from copy import deepcopy | |
dist = [float('inf')] * n | |
# 从 src 开始 所以 src 到它自己为 0 | |
dist[src] = 0 | |
# 细节:这里要循环 k+1 次 是因为落地城市也要算上一个 | |
for i in range(k + 1): | |
back = deepcopy(dist) | |
for a, b, w in flights: | |
dist[b] = min(dist[b], back[a] + w) | |
return -1 if dist[dst] == float('inf') else dist[dst] |