# 前置知识

看完必会的并查集入门攻略。本文是上篇文章的延伸，并查集的实战应用篇。

目录

AcWing 1250. 格子游戏：二维坐标的并查集裸替，主要考察二维坐标转一维。

AcWing 1252. 搭配购买：使用并查集把相同集合的多个物品看做一个整体，方便使用 01 背包。

AcWing 237. 程序自动分析：带有离散化的并查集。

AcWing 238. 银河英雄传说：维护额外信息（距离和个数）的并查集。

AcWing 239. 奇偶游戏：综合应用。带有边权的并查集和带有扩展域的并查集，同时也应用了离散化。

# AcWing 1250. 格子游戏

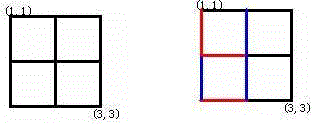
Alice 和 Bob 玩了一个古老的游戏：首先画一个 n×n 的点阵（下图 n=3）。接着，他们两个轮流在相邻的点之间画上红边和蓝边： 直到围成一个封闭的圈（面积不必为 1）为止，“封圈” 的那个人就是赢家。因为棋盘实在是太大了，他们的游戏实在是太长了！他们甚至在游戏中都不知道谁赢得了游戏。于是请你写一个程序，帮助他们计算他们是否结束了游戏？

输入格式

输入数据第一行为两个整数 n 和 m。n 表示点阵的大小，m 表示一共画了 m 条线。以后 m 行，每行首先有两个数字 (x,y)，代表了画线的起点坐标，接着用空格隔开一个字符，假如字符是 D，则是向下连一条边，如果是 R 就是向右连一条边。输入数据不会有重复的边且保证正确。

输出格式

输出一行：在第几步的时候结束。假如 mm 步之后也没有结束，则输出一行 “draw”。

数据范围

1≤n≤200，
1≤m≤24000

输入样例

3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D

输出样例

4

# 题目描述

在一个 n*n 的点阵上画边，一人画一次，问什么时候可以得到一个封闭的矩形。

# 题目分析

一人一画的规则有点像博弈论的问题，但是读到最后，我们发现并没有问，最后赢的人是谁，而是问什么时候完成封闭矩形的。

这样一来就比较简单了。我们可以使用并查集的思路来解决。

初始的时候，每个点都是单独属于一个集合，把两点连接一条边看做是把两点加入到一个集合里。这样一来，假如连完边之后，形成了一个矩形，说明在连边之前，这两个点一定已经在一个集合中。

因此，本题其实只需要在合并之前，判断一下两个点是否在同一个集合，就可以知道连完之后会不会出现封闭矩阵。

# Code

实现的时候，需要注意的一点是：题目给出的点是二维的，我们需要转换成一维。

二维转一维的公式是： x坐标 * n + y坐标 (其中 x 和 y 必须从 0 开始)。

#include <iostream>

#include <cstring>

using namespace std;

const int N = 40010, M = 24010;

int n, m;

int p[N], res;

int find(int x) {

    if (p[x] != x) p[x] = find(p[x]);

    return p[x];

}

// 二维点坐标变成一维

int get(int x, int y) {

    return x * n + y;

}

int main() {

    cin >> n >> m;

    for (int i = 0; i <= n * n; i ++ ) p[i] = i;

    for (int i = 1; i <= m; i ++ ) {

        int x, y;

        char t;

        cin >> x >> y >> t;

        // 二维转一维 坐标必须从 0 开始 不然不满足公式

        x -- , y -- ;

        int a = get(x, y); 

        int b;

        if (t == 'D') b = get(x + 1, y);

        else b = get(x, y + 1);

        int pa = find(a), pb = find(b);

        // 两个点在同一集合 则连边后形成封闭矩阵

        if (pa == pb) {

            res = i;

            break;

        }

        p[pa] = pb; // 不在同一集合 合并两条边

    }

    if (!res) puts("draw");

    else cout << res << endl;

    return 0;

}

# AcWing 1252. 搭配购买

Joe 觉得云朵很美，决定去山上的商店买一些云朵。商店里有 n 朵云，云朵被编号为 1,2,…,n 并且每朵云都有一个价值。但是商店老板跟他说，一些云朵要搭配来买才好，所以买一朵云则与这朵云有搭配的云都要买。但是 Joe 的钱有限，所以他希望买的价值越多越好。

输入格式

第 1 行包含三个整数 n，m，w 表示有 n 朵云，m 个搭配，Joe 有 w 的钱。第 2∼n+1 行，每行两个整数 ci，di 表示 i 朵云的价钱和价值。第 n+2∼n+1+m 行，每行两个整数 ui，vi 表示买 ui 就必须买 vi，同理，如果买 vi 就必须买 ui。

输出格式

一行，表示可以获得的最大价值。

数据范围

1≤n≤10000,
0≤m≤5000,
1≤w≤10000,
1≤ci≤5000,
1≤di≤100,
1≤ui,vi≤n

输入样例

5 3 10
3 10
3 10
3 10
5 100
10 1
1 3
3 2
4 2

输出样例

1

# 题目描述

（买云朵的故事真是太浪漫啦～～）

一些云朵需要搭配起来购买，总共有 n 朵云，m 个搭配，Joe 同学有 w 块钱，每个云朵都有价钱和价值两种属性，问怎么买才能获得最大价值的云朵。

# 题目分析

一眼看上去非常的像有 依赖的背包问题 ，但是我们仔细的读题，会发现与依赖背包还是不太一样，对于本题来说，如果有一个云朵被买，那么所有与该云朵搭配的云朵都需要一起被买（而依赖背包中是只有父节点被购买，才需要子节点也购买，反过来，子节点购买，是不需要购买父节点的），这就启发我们，把所有搭配的云朵看做一个集合（并查集的集），然后把每个集合作为一个商品，这样本题就变成了 01 背包问题。

# Code

#include <iostream>

#include <cstring>

using namespace std;

const int N = 10010;

int p[N], w[N], v[N], f[N];

int n, m, money;

int find(int x) {

    if (p[x] != x) p[x] = find(p[x]);

    return p[x];

}

int main() {

    cin >> n >> m >> money;

    for (int i = 1; i <= n; i ++ ) p[i] = i;

    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    while (m -- ) {

        int a, b;

        cin >> a >> b;

        int pa = find(a); int pb = find(b);

        // 合并一个集合里的云朵 价格和价值 别忘记合并

        if (pa != pb) {

            w[pa] += w[pb];

            v[pa] += v[pb];

            p[pb] = pa;

        }

    }

    // 01 背包模板

    for (int i = 1; i <= n; i ++ ) {

        if (p[i] == i)

            for (int j = money; j >= v[i]; j -- )

                f[j] = max(f[j], f[j - v[i]] + w[i]);

    }

    cout << f[money] << endl;

    return 0;

}

# AcWing 237. 程序自动分析

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 x1,x2,x3,… 代表程序中出现的变量，给定 n 个形如 xi=xj 或 xi≠xj 的变量相等 / 不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。

例如，一个问题中的约束条件为：x1=x2，x2=x3，x3=x4，x1≠x4，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式
输入文件的第 1 行包含 1 个正整数 t，表示需要判定的问题个数，注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第 1 行包含 1 个正整数 n，表示该问题中需要被满足的约束条件个数。

接下来 n 行，每行包括 3 个整数 i,j,e，描述 1 个相等 / 不等的约束条件，相邻整数之间用单个空格隔开。若 e=1，则该约束条件为 xi=xj；若 e=0，则该约束条件为 xi≠xj。

输出格式
输出文件包括 t 行。

输出文件的第 k 行输出一个字符串 YES 或者 NO，YES 表示输入中的第 k 个问题判定为可以被满足，NO 表示不可被满足。

数据范围
1≤n≤10^5
1≤i,j≤10^9

输入样例

2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出样例

NO
YES

# 题目分析

给出一些约束条件，这些约束条件分为两个种类，一种是等于，一种是不等于，问题是给出的约束条件能否同时满足。

# 题目分析

本题第一眼看上去，有些像差分约束问题，但是我们发现本题的约束条件只有两种，一种等于，一种不等于，所以我们完全没必要把约束条件转换成图。

我们发现这两种类型的数据具有明显的传递关系，那就可以把这两种关系类型的数据用集合维护起来，等于号的在一个集合，不等于号的在另一个集合，这样只要集合出现冲突就说明这个问题可以被判定为不满足条件。

而维护具有传递关系的集合，我们就可以使用并查集。

例如题面给出的示例： x1=x2，x2=x3，x3=x4，x1≠x4 ，我们先把所有相等关系的数据合并到一个集合中，那么在所有的不等关系的数据中，只要两个数据在同一个集合内，就说明发生冲突，比如 x1 和 x4 。

# Code

本题虽然看起来是一个并查集的裸题，但是其实难点并不在并查集，而是隐藏在数据范围中。

本题的约束条件数量 n 总共有$10^6$ 个，每个约束条件有两个数据，也就是说数据最多也就只会有$2*10^6$ 个，可是单个数据的最大值却达到了$10^9$，那么对于并查集数组来说，就需要$10^9$ 的空间大小，这显然是不可行的。所以，我们需要使用离散化把的单个数据的大小映射到最大为$10^6$。

离散化的作用：当出现数据范围很大，但是能用到的很小的时候，可以使用 离散化 把 数据范围 压缩到 使用范围。

比如，本题把单个数据最大$10^9$ 压缩到单个数据最大$10^6$。

离散化一般分为两种：保持数据顺序的离散化和不保序的离散化。

保序的离散化一般要分为三个步骤：排序、判重、二分。

不保序的离散化比较简单可以使用 map 或者 hash表 之类的数据结构实现即可。

（离散化不是本文重点，因此不做过多讲述，代码中有注释。）

#include <iostream>

#include <cstring>

#include <unordered_map>

using namespace std;

const int N = 2000010;

int n, m;

int p[N];

unordered_map<int, int> S; // 离散化 hash 表

struct Query {

    int x, y, e;

}query[N];

// 超级简单的不保序离散化

// 将单个数据范围在 1~10^9 压缩到 单个数据范围在 1~10^6

int get(int x) {

    // 如果 x 不在哈希表中 就给它一个映射值。

    if (S.count(x) == 0) S[x] = ++ n;

    return S[x]; // 返回 x 在哈希表的位置

}

int find(int x) {

    if (p[x] != x) p[x] = find(p[x]);

    return p[x];

}

int main() {

    int T;

    cin >> T;

    while (T -- ) {

        cin >> m;

        n = 0;

        S.clear();

        for (int i = 0; i < m; i ++ ) {

            int a, b, c;

            scanf("%d%d%d", &a, &b, &c);

            query[i] = {get(a), get(b), c};

        }

        for (int i = 1; i <= n; i ++ ) p[i] = i;

        // 合并 所有的 相等约束条件

        for (int i = 0; i < m; i ++ ) {

            if (query[i].e == 1) {

                int pa = find(query[i].x);

                int pb = find(query[i].y);

                p[pa] = pb;

            }

        }

        // 检查不等条件

        bool flag = false;

        for (int i = 0; i < m; i ++ ) {

            if (query[i].e == 0 ) {

                int pa = find(query[i].x);

                int pb = find(query[i].y);

                // 在同一个集合说明相等 与 不等条件冲突

                if (pa == pb) { 

                    flag = true;

                    break;

                }

            }

        }

        if (flag) puts("NO");

        else puts("YES");

    }

    return 0;

}

# AcWing 238. 银河英雄传说

有一个划分为 N 列的星际战场，各列依次编号为 1,2,…,N。有 N 艘战舰，也依次编号为 1,2,…,N，其中第 i 号战舰处于第 i 列。有 T 条指令，每条指令格式为以下两种之一：

1. M i j ，表示让第 i 号战舰所在列的全部战舰保持原有顺序，接在第 j 号战舰所在列的尾部。
2. C i j ，表示询问第 i 号战舰与第 j 号战舰当前是否处于同一列中，如果在同一列中，它们之间间隔了多少艘战舰。

现在需要你编写一个程序，处理一系列的指令。

输入格式

第一行包含整数 T，表示共有 T 条指令。接下来 T 行，每行一个指令，指令有两种形式： M i j 或 C i j 。其中 M 和 C 为大写字母表示指令类型，i 和 j 为整数，表示指令涉及的战舰编号。

输出格式

你的程序应当依次对输入的每一条指令进行分析和处理：如果是 M i j 形式，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；如果是 C i j 形式，你的程序要输出一行，仅包含一个整数，表示在同一列上，第 i 号战舰与第 j 号战舰之间布置的战舰数目，如果第 i 号战舰与第 j 号战舰当前不在同一列上，则输出−1。

数据范围

N≤30000,T≤500000

输入样例

4
M 2 3
C 1 2
M 2 4
C 4 2

输出样例

-1
1

# 题目描述

并查集的模型，加了一个题面，有 N 个集合，初始化时候，每个集合有一个元素。给出两种命令，一种是合并，一种是查询，不过这个合并的规则是必须是 a 和并到 b 上，也就 a 的父节点是 b。而查询的也不仅仅是两个数是否在一个集合，而是当两个数据在一个集合的时候输出这两个数据的 之间有多少个数据。

本题题面隐性表达了非常重要的一点，那就是本题的所有集合均是链，因为所有的合并都是合并到集合的末尾。（后面的分析如果不明白就可以思考一下，集合是链的含义。）

# 题目分析

比较裸的一个并查集题目。主要的难点在于如何维护并查集中数据的位置。

在基础篇中，我们已经讲解过，使用 size 数组维护集合中元素的数量。而本题还需要配合一个另外的数组 d ，来维护并查集中元素到它的根节点的距离。

d [x]：表示集合中的元素 x 到它的根节点 p [x] 的距离。

维护这个距离的意义是什么呢？

试想一下，我们想求的是一个集合中 a 和 b 之间的距离，那么我们只要知道它俩分别到根节点的距离，用这两个距离做差就求出来了。

比如，x 和 y 在一个集合，x 到根节点的距离 d[x]=4 ，而 y 到根节点的距离 d[y]=7 ，那么很明显它俩之间的数据就是 d[x]-d[y] 的绝对值减一，也就是它俩之间有两个元素（5 和 6）。

那么，现在的问题就变成了如何维护距离数组 d 呢？

首先考虑，两个集合的合并，假设我们把集合 x 合并到了集合 y 上面。

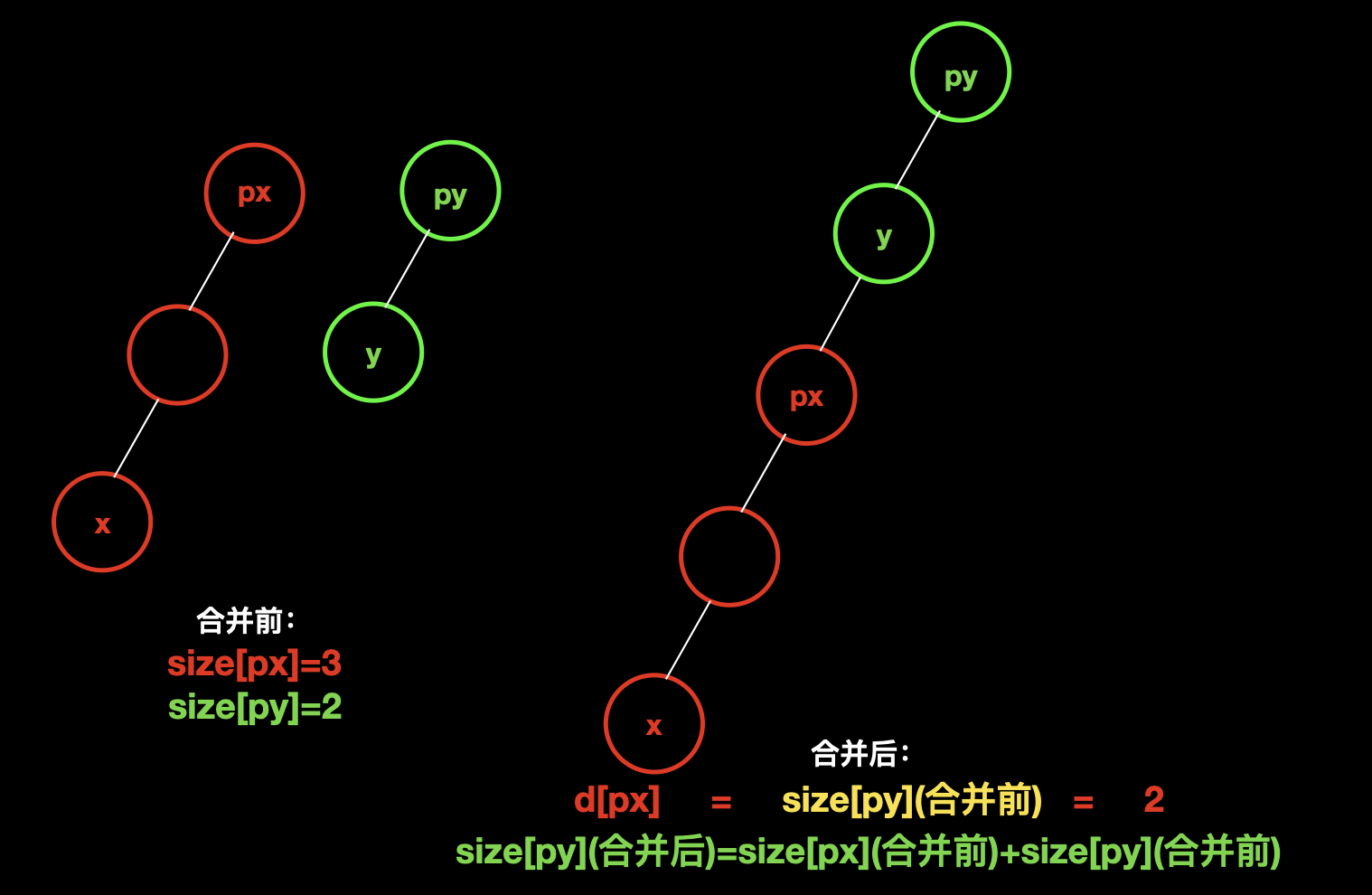
通过图中，我们能直观的看到合并的情况，当集合 px 合并到 py，那么 p [x] 到根节点的距离 就是 合并前 py 中 的所有数据，而合并后，集合 px 就消失了，只剩下集合 py，py 中的数据数量就是 两个集合的数量之和。

除此之外，在合并的时候，在上面的合并上，我们其实并没有求出每个点到根节点的距离，那么我们就可以在，路径优化的时候，来维护每个节点到根节点的距离。

在路径优化维护距离的时候，我们虽然不知道每个距离到根节点的距离，但是我们可以用自底向上的递归，从根节点出发来更新每个节点的距离。

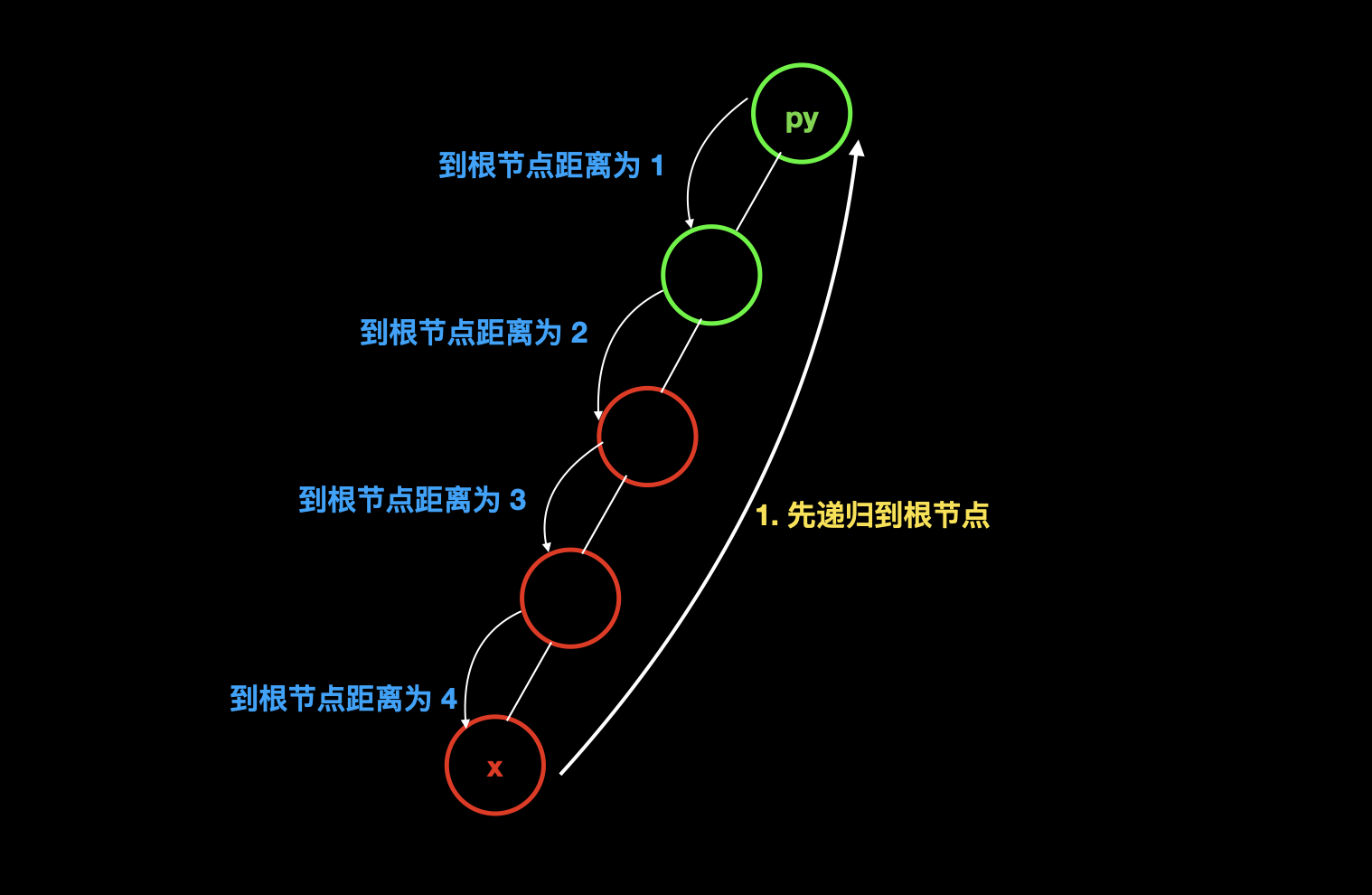
综上，我们就维护出了一个每个元素到根节点的距离的数组 d。

# Code

#include <iostream>

#include <cstring>

using namespace std;

const int N = 300010;

int n, m, p[N], sz[N], d[N];

// 维护距离的并查集模板

int find(int x) {

    if (p[x] != x) {

        int root = find(p[x]); // 先递归到根节点

        d[x] += d[p[x]];  // 根节点开始累加

        p[x] = root;

    }

    return p[x];

}

int main() {

    cin >> m;

    // 初始化 每个节点到自身的距离为 0 

    // 初始化 每个集合中的数据个数为 1 也就是根节点自己

    for (int i = 1; i <= N; i ++ )

        p[i] = i, d[i] = 0, sz[i] = 1;

    while (m -- ) {

        int a, b;

        char t;

        cin >> t >> a >> b;

        int pa = find(a), pb = find(b);

        if (t == 'M') {

            // 当两个数据不在一个集合 则合并

            if (pa != pb) {

                // 合并 且维护信息

                p[pa] = pb;

                d[pa] = sz[pb];

                sz[pb] += sz[pa];

            }

        } else {

            if (pa != pb) cout << -1 << endl;

            else {

                // 注意输出的时候 因为减一的关系 可能会负

                // 但是有解情况 最小是 0 也就是自己到自己

                cout << max(abs(d[a] - d[b]) - 1, 0) << endl;

            }

        }

    }

    return 0;

}

# AcWing 239. 奇偶游戏

小 A 和小 B 在玩一个游戏。首先，小 A 写了一个由 0 和 1 组成的序列 S，长度为 N。然后，小 B 向小 A 提出了 M 个问题。在每个问题中，小 B 指定两个数 l 和 r，小 A 回答 S [l∼r] 中有奇数个 1 还是偶数个 1。机智的小 B 发现小 A 有可能在撒谎。例如，小 A 曾经回答过 S [1∼3] 中有奇数个 1，S [4∼6] 中有偶数个 1，现在又回答 S [1∼6] 中有偶数个 1，显然这是自相矛盾的。请你帮助小 B 检查这 M 个答案，并指出在至少多少个回答之后可以确定小 A 一定在撒谎。即求出一个最小的 k，使得 01 序列 S 满足第 1∼k 个回答，但不满足第 1∼k+1 个回答。

输入格式

第一行包含一个整数 N，表示 01 序列长度。第二行包含一个整数 M，表示问题数量。接下来 M 行，每行包含一组问答：两个整数 l 和 r，以及回答 even 或 odd ，用以描述 S [l∼r] 中有偶数个 1 还是奇数个 1。

输出格式

输出一个整数 k，表示 01 序列满足第 1∼k 个回答，但不满足第 1∼k+1 个回答，如果 01 序列满足所有回答，则输出问题总数量。

数据范围

N≤109,M≤5000

输入样例

10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd

输出样例

3

# 题目描述

一个有趣的游戏，小 A 给出一个 01 序列 S，小 B 问小 A 一个区间 [l,r] 内有多少个 1。但是小 B 发现小 A 可能会说谎，比如小 A 说区间 [1,3] 中有奇数个 1，[4,6] 有偶数个 1，那么奇数 加上 偶数 则一定有 奇数个 1，也就是区间 [1,6] 一定有奇数个 1，可是小 A 又说 [1,6] 有偶数个 1，所以小 A 说谎了。

问题是给出 M 个回答，问小 B 在第几个回答的时候发现小 A 说慌了。

# 题目分析

本题给出的是一个区间的奇偶性，对于整个区间而言是不太好分析的，所以使用类似前缀和的思想，将区间转换为变量。

使用 sum [i] 表示 1~i 中 1 的个数的奇偶数组。则有：

1. S [L,R] 有偶数个 1，等价于 sum [L-1] 与 sum [R] 的奇偶性相同。例如，示例中有 S [1,3] 有奇数个 1，S [4,6] 有偶数个 1。而区间 S [4,6] 又可以拆分成 sum [3] 和 sum [6]，并且他们两个奇偶性应该相同，而 sum [3] 就是区间 S [1,3] 是奇数，所以 sum [6] 就是区间 S [1,6] 也应该是奇数。

2. S [L,R] 有奇数个 1，等价于 sum [L-1] 与 sum [R] 的奇偶性不同。与上面同理。

注意在上面的思路中，我们并没有求出整个 sum 数组，只是把 sum [3] 和 sum [6] 看做一个变量。

如此，我们就构造出了数据的传递关系，因此，我们就可以参考上题的思路，使用并查集来解决。

但是与上题相比，本题有三种关系：

1. 如果 x1 和 x2 的奇偶性相同，x2 和 x3 奇偶性也相同，那么 x1 和 x3 奇偶性相同；

2. 如果 x1 和 x3 的奇偶性相同，x2 和 x3 奇偶性不同，那么 x1 和 x3 奇偶性不同；

3. 如果 x1 和 x2 的奇偶性不同，x2 和 x3 奇偶性也不同，那么 x1 和 x3 的奇偶性相同；

我们神奇的发现，如果把奇偶性相同看做 1，不同看做 0，那么这不就是异或的运算规则嘛？

对于这种多种传递关系的并查集，一种解决方案是使用带边权的并查集，还有一种解决方案是使用带扩展域的并查集。

# 带边权的并查集

我们可以参考一下上一道题，在上一道题中，同样是判断矛盾，当发现不等式组的两个数据在同一个集合中，我们就认为是矛盾。但是在本题中，我们还需要知道这两个数据在这个集合中的奇偶关系是否什么样的。

那么如何维护一个集合中不同数据的关系呢？

我们可以让集合中的每个数据都与根节点产生关联，以此间接的使所有的数据关联到一起。

比如：a 与根节点奇偶性不同，b 与根节点奇偶性相同，则我们可以知道 a 与 b 奇偶性不同。

所以，在路径优化的过程中，就可以把每个数据与根节点的关系维护出来，也就是带有边权的并查集。

带有边权的并查集，使用一个数组 d[x] 维护数据 x 与根节点 p[x] 的相对关系。

在本题中，边权 d [x] 为 0 表示与根节点 p [x] 的奇偶性相同，为 1 表示与根节点 p [x] 的奇偶性不同。

综上，我们总结一下本题的思路：

1. 对于给定的每个区间，我们判断 sum [L] 和 sum [R] 是否属于一个集合（奇偶性关系已知）。

2. 属于一个集合的话，判断他们在集合内的奇偶关系与给出的奇偶关系是否相同，如果不相同，说明出现矛盾，小 A 说谎了。

3. 如果不属于一个集合，则将两个数据合并。

# 带扩展域的并查集

我们把变量 X 拆分成两个节点，一个是 Xodd，一个是 Xeven。其中 Xodd 表示 sum [X] 是奇数，Xeven 表示 sum [X] 是偶数，我们一般也会把这两个节点分别称为奇数域和偶数域。

在带扩展域的并查集中，我们要合并的就是这些域，而非数据本身。

假设，题目给出区间 [L,R] 的奇偶性是 ans，并且 sum [L-1] 和 sum [R] 离散化之后是 x 和 y，假设，我们让 ans 为 0 表示偶数，1 表示奇数。

那么当 ans 等于 0 的时候，合并 Xodd,Yodd ，合并 Xeven,Yeven ，表示当 X 和 Y 的奇偶性相同的时候，可以互相推出，既知道 X 是偶数，则 Y 也是偶数；知道 X 是奇数，则 Y 也是奇数。

当 ans 等于 1 的时候，合并 Xodd,Yeven ，合并 Xeven,Yodd ，表示当 X 和 Y 奇偶性不同的时候，可以互相推出。

我们的想一下，这样做有什么好处呢？

我们把使用并查集 维护数据 变成了 维护条件，也就是我们本来维护的是 X 和 Y，现在变成了维护 X 是偶数，Y 是奇数等条件。

这样做，当我们知道 X 与 Y 的关系之后，如果又知道了 Y 与 Z 的关系，那么我们也就知道了 X 与 Z 的关系，也就是这些条件具有传递性。

比如，通过数据 x,y,0 推出 X 和 Y 的奇偶性相同，再来一个数据 y,z,1 推出 Y 和 Z 奇偶性不同，我们就可以得到 x,z,1 表示 X 与 Z 的奇偶性也是不同的。

那么，我们如何判断矛盾呢？

假如两个变量 X 和 Y，有 Xodd 和 Yodd 在一个集合，说明两者奇偶性必定相同；如果 Xodd 和 Yeven 在一个集合里说明两者奇偶性是不同的，那么如果新数据与之相悖，说明出现了矛盾。

# Code

在实现上，由于本题的数据范围也是比较奇怪，N 的长度为$10^9$，但是问答 M 的数量只有$10^5$，因此也需要使用离散化压缩数据。

# 带边权的并查集

带边权的并查集，在合并时候要更新边权数组 d []。

我们定义 d [x] 表示的是 x 到根节点 p [x] 的关系，d [y] 是 y 到根节点 p [y] 的关系，那么合并的时候，假如是把 x 合并到了 y 上面（以 y 作为集合根节点），那么 x 到根节点的关系就由三部分组成：

1. x 到 x 的原根节点 p [x]，这部分就是 d [x]；

2. x 的原根节点 p [x] 到 y，也就是 d[p[x]] 我们是不知道的，但是我们知道合并后的结果，假设合并后的结果是 t，那么就有 t=d[x]^d[y]^d[p[x]] ，如此，我们就推出了 d[p[x]]=d[x]^d[y]^t ；

3. y 到根节点 p [y]，这部分就是 d [y]；

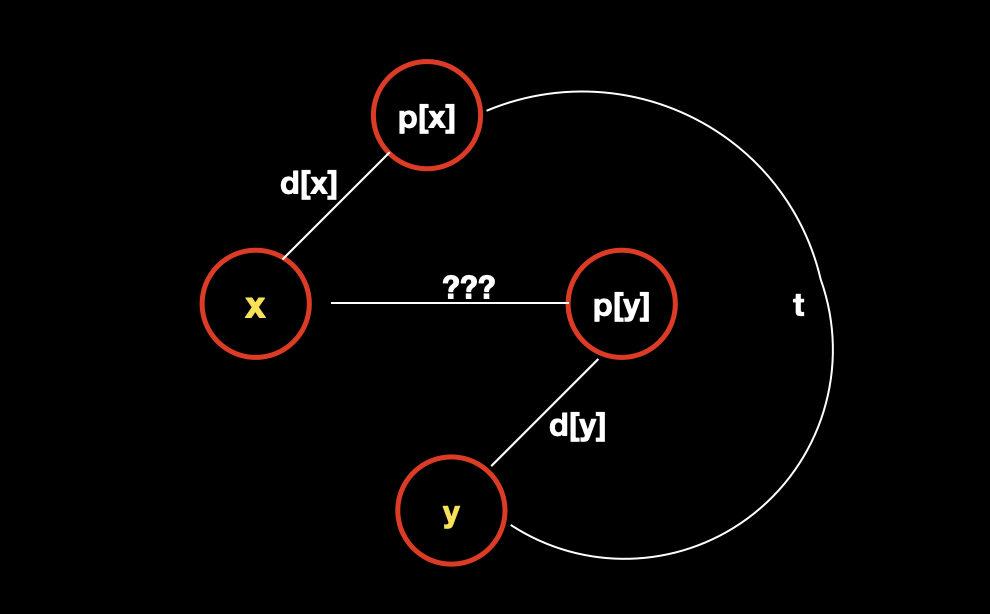
我们把这三部分全部异或起来，就得到了合并后的 d [x]。

#include <iostream>

#include <cstring>

#include <unordered_map>

using namespace std;

const int N = 20010;

int n, m;

int p[N], d[N];

unordered_map<int, int> S;

int find(int x) {

    // 带权并查集的路径压缩 必须注意细节

    // 一定 先计算边权 再压缩

    if (p[x] != x) {

        int root = find(p[x]);

        d[x] ^= d[p[x]];

        p[x] = root;

    }

    return p[x];

}

int get(int x) {

    if (S.count(x) == 0) S[x] = ++ n;

    return S[x];

}

int main() {

    cin >> n >> m;

    n = 0;

    for (int i = 0; i < N; i ++ ) p[i] = i;

    int res = m; // 没有矛盾输出问题的数量

    for (int i = 0; i < m; i ++ ) {

        int a, b;

        string c;

        cin >> a >> b >> c;

        // 获取离散化后的 sum [L-1] 和 sum [R]

        a = get(a - 1), b = get(b);

        int t = 0; // 0 表示偶数个 1

        if (c == "odd") t = 1; // 1 表示有奇数个 1

        int pa = find(a), pb = find(b);

        // 如果两个数据的奇偶关系已知

        if (pa == pb) {

            // 判断他们的奇偶关系 是否和本次数据相同

            if ((d[a] ^ d[b]) != t) {

                res = i;

                break;

            }

        } else {

            p[pa] = pb;

            // 并查集到根

            d[pa] = d[a] ^ d[b] ^ t;

        }

    }

    cout << res << endl;

    return 0;

}

# 带扩展域的并查集

在实现上，我们如何表示两个点呢？

可以直接用两个不同的数，假如数据为 X，那么我们可以让 X 本身来表示 Xeven，用 X+Base 来表示 Xodd（这里的 Base 为数据总量除以 2，所以 X+Base 是一个一定不在本题使用范围内的数，因此保证了数据不会重复）。

#include <iostream>

#include <cstring>

#include <unordered_map>

using namespace std;

const int N = 20010, Base = N / 2;

int n, m;

int p[N], d[N];

unordered_map<int, int> S;

int find(int x) {

    if (p[x] != x) p[x] = find(p[x]);

    return p[x];

}

int get(int x) {

    if (S.count(x) == 0) S[x] = ++ n;

    return S[x];

}

int main() {

    cin >> n >> m;

    n = 0;

    for (int i = 0; i < N; i ++ ) p[i] = i;

    int res = m; // 没有矛盾输出问题的数量

    for (int i = 0; i < m; i ++ ) {

        int a, b;

        string c;

        cin >> a >> b >> c;

        // 获取离散化后的 sum [L-1] 和 sum [R]

        a = get(a - 1), b = get(b);

        int t = 0; // 0 表示偶数个 1

        // 假如给出数据是 X 和 Y 是偶数关系

        // 则有 Xodd 和 Yodd 在一个集合 Xeven 和 Yeven 在一个集合

        if (c == "even") {

            // 如果 Xodd 和 Yeven 在一个集合 一定矛盾

            if (find(a + Base) == find(b)) {

                res = i;

                break;

            }

            p[find(a)] = p[find(b)]; // Xodd 和 Yodd 合并到一个集合

            p[find(a + Base)] = p[find(b + Base)]; // Xeven 和 Yeven 合并到一个集合

        } else {

            // 反之，则相反

            if (find(a) == find(b)) {

                res = i;

                break;

            }

            p[find(a)] = p[find(b + Base)]; // Xeven 和 Yodd 在一个集合

            p[find(a + Base)] = p[find(b)]; // Xodd 和 Yeven 在一个集合

        }

    }

    cout << res << endl;

    return 0;

}

END