# 欧拉路径和欧拉回路
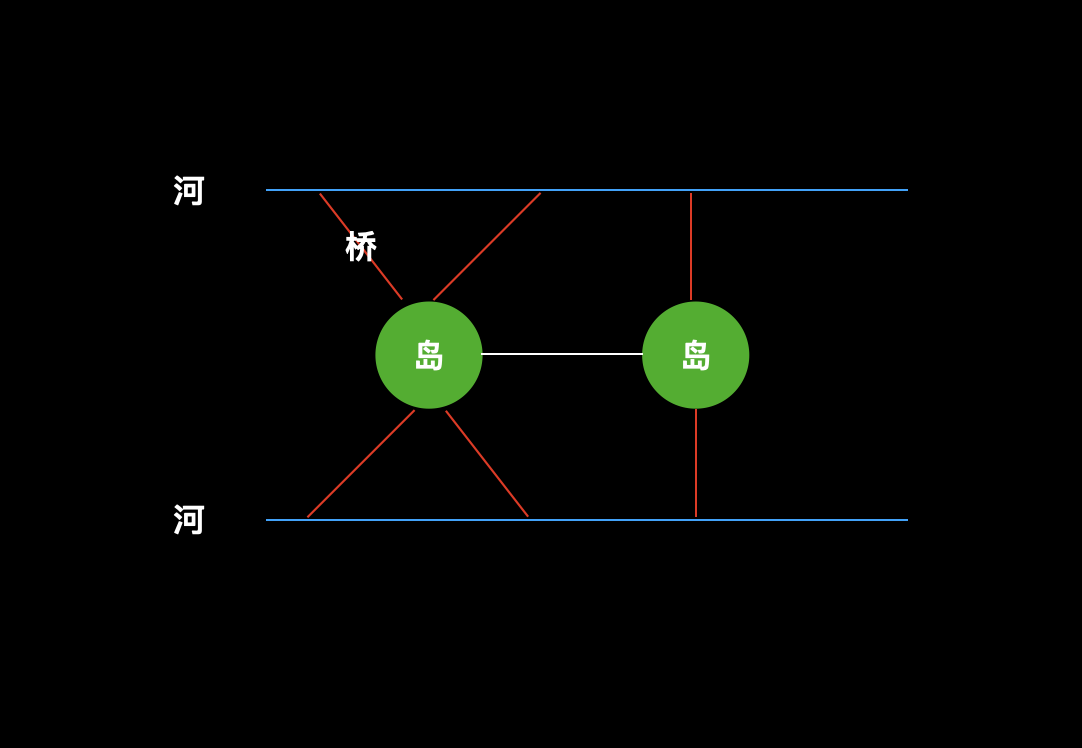
哥尼斯堡七桥问题:18 世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来(如概述图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。后来大数学家欧拉把它转化成一个几何问题 —— 一笔画问题。
在图论的概念里,我们把这个一笔画问题称为欧拉路径问题。
欧拉路径问题:是否存在一个路劲,使得每条边 恰好 走一次。
欧拉回路问题:是否存在一个环路,使得每条边 恰好 走一次。
# 欧拉路径和欧拉回路的成立条件
我们先把七桥问题转换成图,于是可以得到如下图: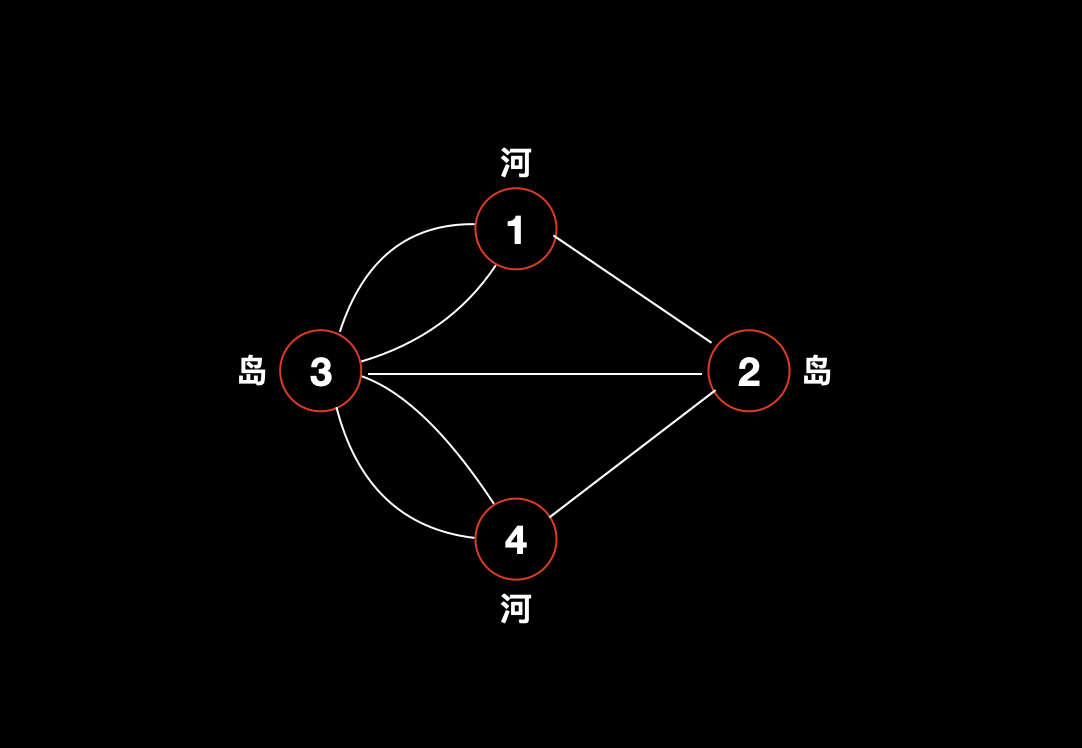
我们发现四个点的度分别是: 3、3、5、3 。
我们发现对于 起点的度 来说,从起点初始延伸出一条出边,而后其他的边再经过起点,必定是进去之后还要出来,也就是度一定是偶数,那么算上起点初始延伸出去的那条边,最终起点的度一定是奇数。
而对于 终点的度 来说,除了最终走到它的那条边之外,其他所有经过它的边,必定也是进去之后再出来,所以同 起点的度 一样,终点的度也一定是奇数。
对于路径中所有 中间点的度 来说,走进来之后一定就要走出来,所以中间点的度 一定是偶数。
因此,我们就能得出一些关于欧拉路径问题的结论:
对于无向图来说:
欧拉路径问题成立的充分必要条件:度数为奇数的点只能有 0 个或者 2 个;
欧拉回路问题成立的充分必要条件:我们把欧拉回路看成是一种特殊的欧拉路径,因为起点也是终点,所以起点的度也必须是偶数。于是得到结论度数为奇数的点只能有 0 个;
对于有向图(所有边都连通)来说:
存在欧拉函数的充分必要条件:要么所有点的出度均等于入度;要么除了两个点之外,其余所有点的出度等于入度。剩余的两个点,起点满足出度比入度多 1,终点满足入度比出度多 1。
存在欧拉回路的充分必要条件:所有点的出度都等于入度。
# 基础思路
int seq[N]; // 存储最终的路径序列 | |
void dfs(u) { | |
for (int i = h[u]; ~i; i = ne[i]) { | |
dfs(e[i]); // 扩展 | |
} | |
把u加入序列 seq[]←u | |
} |
最后, seq[] 中存下的就是欧拉路径的倒序。
# AcWing 1123. 铲雪车
随着白天越来越短夜晚越来越长,我们不得不考虑铲雪问题了。
整个城市所有的道路都是双向车道,道路的两个方向均需要铲雪。因为城市预算的削减,整个城市只有 1 辆铲雪车。
铲雪车只能把它开过的地方(车道)的雪铲干净,无论哪儿有雪,铲雪车都得从停放的地方出发,游历整个城市的街道。
现在的问题是:最少要花多少时间去铲掉所有道路上的雪呢?
输入格式
输入数据的第 1 行表示铲雪车的停放坐标 (x,y),x,y 为整数,单位为米。下面最多有 4000 行,每行给出了一条街道的起点坐标和终点坐标,坐标均为整数,所有街道都是笔直的,且都是双向车道。
铲雪车可以在任意交叉口、或任何街道的末尾任意转向,包括转 U 型弯。
铲雪车铲雪时前进速度为 20 千米 / 时,不铲雪时前进速度为 50 千米 / 时。
保证:铲雪车从起点一定可以到达任何街道。
输出格式
输出铲掉所有街道上的雪并且返回出发点的最短时间,精确到分钟,四舍五入到整数。输出格式为”hours:minutes”,minutes 不足两位数时需要补前导零。
具体格式参照样例。数据范围
−10^6≤x,y≤10^6 所有位置坐标绝对值不超过 10^6。输入样例
0 0 0 0 10000 10000 5000 -10000 5000 10000 5000 10000 10000 10000输出样例
3:55样例解释
输出结果表示共需3小时55分钟。
# 题目描述
一个城市铲雪的问题,这个城市因为预算只有一辆铲雪车啦(可以说是非常穷了)。
一个城市有很多双向道路,铲雪车从一个起点开始沿着道路走,所有它走过的地方会被铲掉,因为是双向道路,所以两个方向均需要铲雪,铲雪车需要过去一趟,回来一趟,才能铲完一条道路上的雪。铲雪车在任意街道的末尾或者交叉口,可以随意转向,问题是最少需要多少时间可以铲除所有道路上的雪。
# 题目分析
我们以图中点 b 为参照点,可以发现,因为每条道路都是双向的,也就是说,假如另一个到达 b 的点是 a ,那么 a->b 会为 b 提供一个入度,而 b->a 会为 b 提供一个出度,也就是说对于点 b 来说,有一个出度就会有一个入度,它的出入度永远是成对出现的,也就是说永远不可能出现单数(奇数)。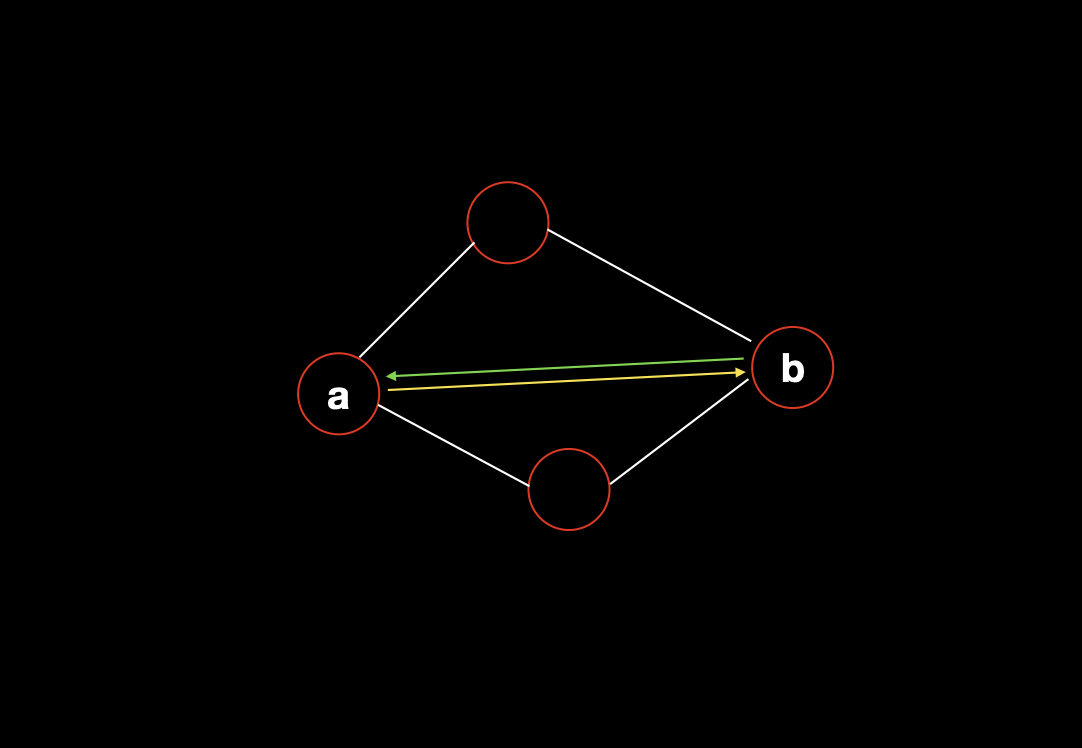
进而,我们发现其实任意一个点都满足上面得出来的结论:所有点的度都不是奇数,说明题目给出的图,其实是一个欧拉回路,那么我们就一定有办法,每条路都只走一遍(一个来回),就可以铲完所有雪。
也就是二倍的所有路径总长度 除以 铲雪速度:。
所以,本题虽然是个图论问题,但是更向一个脑筋急转弯,我们用欧拉回路的性质,可以直接算出来结果。
# Code
#include <iostream> | |
#include <cstring> | |
#include <cmath> | |
using namespace std; | |
int main() { | |
double x1, y1, x2, y2; | |
cin >> x1 >> y1; | |
double sum = 0; | |
while (cin >> x1 >> y1 >> x2 >> y2) { | |
double dx = x1 - x2; | |
double dy = y1 - y2; | |
sum += sqrt(dx * dx + dy * dy) * 2; | |
} | |
// 转换成千米 除以速度 再转换成小时 round 是四舍五入 | |
int minutes = round(sum / 1000 / 20 * 60); | |
int hours = minutes / 60; | |
minutes %= 60; | |
printf("%d:%02d\n", hours, minutes); | |
return 0; | |
} |
# AcWing 1184. 欧拉回路
给定一张图,请你找出欧拉回路,即在图中找一个环使得每条边都在环上出现恰好一次。
输入格式
第一行包含一个整数 t,t∈{1,2},如果 t=1,表示所给图为无向图,如果 t=2,表示所给图为有向图。第二行包含两个整数 n,m,表示图的结点数和边数。
接下来 m 行中,第 i 行两个整数 vi,ui,表示第 i 条边(从 1 开始编号)。
如果 t=1 则表示 vi 到 ui 有一条无向边。
如果 t=2 则表示 vi 到 ui 有一条有向边。
图中可能有重边也可能有自环。点的编号从 1 到 n。
输出格式
如果无法一笔画出欧拉回路,则输出一行:NO。否则,输出一行:YES,接下来一行输出 任意一组 合法方案即可。
如果 t=1,输出 m 个整数 p1,p2,…,pm。令 e=|pi|,那么 e 表示经过的第 i 条边的编号。如果 pi 为正数表示从 ve 走到 ue,否则表示从 ue 走到 ve。
如果 t=2,输出 m 个整数 p1,p2,…,pm。其中 pi 表示经过的第 i 条边的编号。
数据范围1≤n≤105, 0≤m≤2×105输入样例 1
1
3 3
1 2
2 3
1 3
输出样例 1YES 1 2 -3输入样例 2
2 5 6 2 3 2 5 3 4 1 2 4 2 5 1输出样例 2
YES 4 1 3 5 2 6
# 题目描述
纯粹的欧拉回路模板题。
# 题目分析
纯粹的欧拉回路模板题。
有一个需要特别考虑的问题是如何判断无解,我们可以根据性质定义来判断是否有解。
对于无向图来说,有解的话:
- 所有点的度数必须是偶数;
- 所有边必须都是连通的;
对于有向图来说,有解的话:
- 所有点的入度等于出度;
- 所有边连通;
# Code
#include <iostream> | |
#include <cstring> | |
#include <algorithm> | |
using namespace std; | |
const int N = 100010, M = 400010; | |
int n, m, type; | |
int h[N], e[M], ne[M], idx; | |
// 欧拉回路每条边只能使用一次 | |
bool used[M]; // 判断每条边是否使用过 | |
int ans[M], cnt; // 记录路径和路径的长度 | |
int din[N], dout[N]; | |
void add(int a, int b) { | |
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ; | |
} | |
void dfs(int u) { | |
for (int &i = h[u]; ~i;) { | |
if (used[i]) { | |
// 边已经被用过则删掉一条边 | |
i = ne[i]; | |
continue; | |
} | |
used[i] = true; // 标记边 u->i 已经被用过了 | |
// 马上就要用这条边 也把它删掉 | |
// 如果是无向图 同时标记反向边也被用掉了。 | |
if (type == 1) used[i ^ 1] = true; | |
int t; | |
// 把当前边添加到结果 | |
if (type == 1) { | |
// (0,1) (2,3) (4,5) 奇数作为返回的边 | |
t = i / 2 + 1; | |
// 边从 0 开始计数 所以当 i 为奇数的时候是反向边 | |
if (i & 1) t = -t; | |
} else t = i + 1; | |
int j = e[i]; | |
i = ne[i]; | |
dfs(j); | |
ans[ ++ cnt] = t; | |
} | |
} | |
int main() { | |
cin >> type; | |
cin >> n >> m; | |
memset(h, -1, sizeof h); | |
for (int i = 0; i < m; i ++ ) { | |
int a, b; | |
cin >> a >> b; | |
add(a, b); | |
if (type == 1) add(b, a); | |
din[b] ++, dout[a] ++ ; | |
} | |
if (type == 1) { | |
// 如果是无向图 那么每个点的度 必须是偶数 | |
for(int i = 1; i <= n; i ++ ) { | |
if (din[i] + dout[i] & 1) { | |
puts("NO"); | |
return 0; | |
} | |
} | |
} else { | |
// 如果是有向图 那么每个点的入度则必须等于出度 | |
for (int i = 1; i <= n; i ++ ) { | |
if (din[i] != dout[i]) { | |
puts("NO"); | |
return 0; | |
} | |
} | |
} | |
for (int i = 1; i <= n; i ++ ) { | |
// 找到一个存在边的点 作为起点 | |
if (h[i] != -1) { | |
dfs(i); | |
break; | |
} | |
} | |
// 最后的路径如果没有走过所有的边 也失败 | |
if (cnt < m) { | |
puts("NO"); | |
return 0; | |
} | |
puts("YES"); | |
for (int i = cnt; i > 0; i -- ) printf("%d ", ans[i]); | |
puts(""); | |
return 0; | |
} |
# AcWing 1124. 骑马修栅栏
农民 John 每年有很多栅栏要修理。
他总是骑着马穿过每一个栅栏并修复它破损的地方。
John 是一个与其他农民一样懒的人。
他讨厌骑马,因此从来不两次经过一个栅栏。
你必须编一个程序,读入栅栏网络的描述,并计算出一条修栅栏的路径,使每个栅栏都恰好被经过一次。
John 能从任何一个顶点 (即两个栅栏的交点) 开始骑马,在任意一个顶点结束。
每一个栅栏连接两个顶点,顶点用 1 到 500 标号 (虽然有的农场并没有 500 个顶点)。
一个顶点上可连接任意多 (≥1) 个栅栏。
所有栅栏都是连通的 (也就是你可以从任意一个栅栏到达另外的所有栅栏)。
你的程序必须输出骑马的路径 (用路上依次经过的顶点号码表示)。
我们如果把输出的路径看成是一个 500 进制的数,那么当存在多组解的情况下,输出 500 进制表示法中最小的一个 (也就是输出第一个数较小的,如果还有多组解,输出第二个数较小的,等等)。
输入数据保证至少有一个解。
输入格式
第 1 行:一个整数 F,表示栅栏的数目;第 2 到 F+1 行:每行两个整数 i,j 表示这条栅栏连接 i 与 j 号顶点。
输出格式
输出应当有 F+1 行,每行一个整数,依次表示路径经过的顶点号。注意数据可能有多组解,但是只有上面题目要求的那一组解是认为正确的。
数据范围
1≤F≤1024, 1≤i,j≤500输入样例
9 1 2 2 3 3 4 4 2 4 5 2 5 5 6 5 7 4 6输出样例
1 2 3 4 2 5 4 6 5 7
# 题目描述
有很多相互连接的栅栏,一个要走过所有的栅栏,但是每个栅栏它不想走两次,最后输出字典序最小的可行的路径。
也就是给出一个无向图,求字典序最小的欧拉路径。
# 题目分析
本题主要的难点在于求字典序最小。
我们在求欧拉路径的时候,是在自底向上的递归,也就是说先遍历到的点会后加入到路径序列,所以我们只需要保证当前点的所有出边 是 从小到大排序就可以。
# Code
#include <iostream> | |
#include <cstring> | |
using namespace std; | |
const int N = 510; | |
// 数据未给出点数量,但是题目中有说最多 500 个点 | |
int n = 500, m; | |
// 需要从小到大搜索 邻接表比较麻烦 所以用邻接矩阵存图 | |
int g[N][N]; | |
int ans[1100], cnt; | |
int d[N]; | |
void dfs(int u) { | |
for (int i = 1; i <= n; i ++ ) { | |
if (g[u][i]) { | |
// 欧拉路径 每条边只能用一次 | |
// 所以用完就删掉这条无向边 | |
g[u][i] --, g[i][u] --; | |
dfs(i); | |
} | |
} | |
ans[++ cnt] = u; // 加入序列 | |
} | |
int main() { | |
cin >> m; | |
while (m -- ) { | |
int a, b; | |
cin >> a >> b; | |
g[a][b] ++, g[b][a] ++ ; // 无向图 | |
d[a] ++ , d[b] ++ ; | |
} | |
int start = 1; // 找一个起点 | |
// 找到较小的有度数的编号作为起点 | |
while (!d[start]) start ++ ; | |
for (int i = 1; i <= n; i ++ ) { | |
if (d[i] % 2) { | |
start = i; // 较小的奇数点作为起点 | |
break; | |
} | |
} | |
dfs(start); | |
// 因为序列中是反的 所以输出时候也要反向输出结果 | |
for (int i = cnt; i; i -- ) printf("%d\n", ans[i]); | |
return 0; | |
} |
# AcWing 1185. 单词游戏
有 N 个盘子,每个盘子上写着一个仅由小写字母组成的英文单词。
你需要给这些盘子安排一个合适的顺序,使得相邻两个盘子中,前一个盘子上单词的末字母等于后一个盘子上单词的首字母。
请你编写一个程序,判断是否能达到这一要求。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。每组数据第一行包含整数 N,表示盘子数量。
接下来 N 行,每行包含一个小写字母字符串,表示一个盘子上的单词。
一个单词可能出现多次。
输出格式
如果存在合法解,则输出”Ordering is possible.”,否则输出”The door cannot be opened.”。数据范围
1≤N≤105, 单词长度均不超过1000输入样例
3 2 acm ibm 3 acm malform mouse 2 ok ok输出样例
The door cannot be opened. Ordering is possible. The door cannot be opened.
# 题目描述
有 N 个盘子,每个盘子上有一个单词,单词首尾可以拼接,需要我们判断是否可以把所有的单词都拼接到一起。
# 题目分析
假设把单词看做一条边,26 个小写英文字母看做点,那么问题就是能否找到一条路径 依次走过每条边。也就是判断有向图是否存在欧拉路径。
有向图的欧拉路径判断:
- 除了起点和终点外,其余点入度等于出度;
- 是否整个图都连通;
# Code
实现上,判断图是否连通可以使用并查集。
#include <iostream> | |
#include <cstring> | |
using namespace std; | |
const int N = 30; // 26 个字母 | |
int n, m; | |
int din[N], dout[N], p[N]; | |
bool st[N]; | |
int find(int x) { | |
if (p[x] != x) p[x] = find(p[x]); | |
return p[x]; | |
} | |
int main() { | |
char str[1010]; | |
int T; | |
cin >> T; | |
while (T -- ) { | |
cin >> n; | |
memset(st, 0, sizeof st); | |
memset(din, 0, sizeof din); | |
memset(dout, 0, sizeof dout); | |
for (int i = 0; i < 26; i ++ ) p[i] = i; | |
for (int i = 0; i < n; i ++ ) { | |
scanf("%s", str); | |
int len = strlen(str); | |
int a = str[0] - 'a', b = str[len - 1] - 'a'; | |
st[a] = st[b] = true; //ab 已经被使用 | |
dout[a] ++ , din[b] ++ ; | |
p[find(a)] = find(b); | |
} | |
int start = 0, end = 0; // 首尾节点 | |
bool flag = true; // 判断是否成功 | |
// 找到首尾节点 | |
for (int i = 0; i < 26; i ++ ) { | |
// 只有首尾节点可以入度出度不同 | |
if (din[i] != dout[i]) { | |
// 尾节点入度多 1 首节点出度多 1 | |
if (din[i] == dout[i] + 1) end ++ ; | |
else if (din[i] + 1 == dout[i]) start ++ ; | |
// 不是首尾节点 入度出度不同 则说明不是欧拉路径 | |
else { | |
flag = false; | |
break; | |
} | |
} | |
} | |
// 如果找到首尾节点 也需满足条件(见分析)才可以 | |
// if (flag and !((!start and !end) or (start == 1 and end == 1))) flag = false; | |
if (flag && !(!start && !end || start == 1 && end == 1)) flag = false; | |
// 还需要判断连通性 | |
int rep = -1; | |
for (int i = 0; i < 26; i ++ ) { | |
if (st[i]) { | |
if (rep == -1) rep = find(i); // 找唯一祖宗节点 | |
else if (rep != find(i)) { // 有点不属于同一个集合则不连通 | |
flag = false; | |
break; | |
} | |
} | |
} | |
if (flag) puts("Ordering is possible."); | |
else puts("The door cannot be opened."); | |
} | |
return 0; | |
} |
END