# 问题描述

给定一个二分图，其中左半部包含 n1 个点（编号 1∼n1），右半部包含 n2 个点（编号 1∼n2），二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数
1、二分图：在一个图中，可以把所有的点划分到两个集合，满足所有的边都在两个集合之间连通，我们认为这个图是二分图。
2、二分图的匹配：给定一个二分图 G，在 G 的一个子图 M 中，M 的边集 {E} 中的任意两条边都不依附于同一个顶点，则称 M 是一个匹配。
3、二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。
输入格式
第一行包含三个整数 n1、 n2 和 m。
接下来 m 行，每行包含两个整数 u 和 v，表示左半部点集中的点 u 和右半部点集中的点 v 之间存在一条边。
输出格式
输出一个整数，表示二分图的最大匹配数。

# 算法描述

为什么要管这个算法叫 “恋爱循环” 呢？因为它的算法流程和这个名字实在是太像了。这个算法真正的名字叫 “匈牙利算法”，也叫 “增广路算法”。

在这里，我们把一个集合当作男同学集合，一个当作女同学集合。可以连成边的男女同学，就认为是具有好感的。

我们作为 “月老”，任务就是把两个集合中的所有同学两两配对，组合出尽可能多的情侣。

# 算法流程

遍历整个男同学集合，从第一个男同学开始，寻找和他具有好感的女同学，只要找到了就暂时把他俩配成一对。

如果和当前男同学 X 具有好感的女同学 A 已经被配对给了别的同学怎么办呢？此时比较常规的做法是继续去和下一个具有好感的女同学配对。

但是，该算法的做法是找到和这位女同学 A 匹配的男同学 B 是哪位，看下这位男同学 B 是否有其他的女同学 C 可以配对，如果有就让这位男同学 B 和其他人 C 配对。这样当前男同学 X 就可以和女同学 A 进行配对啦。

# 示例

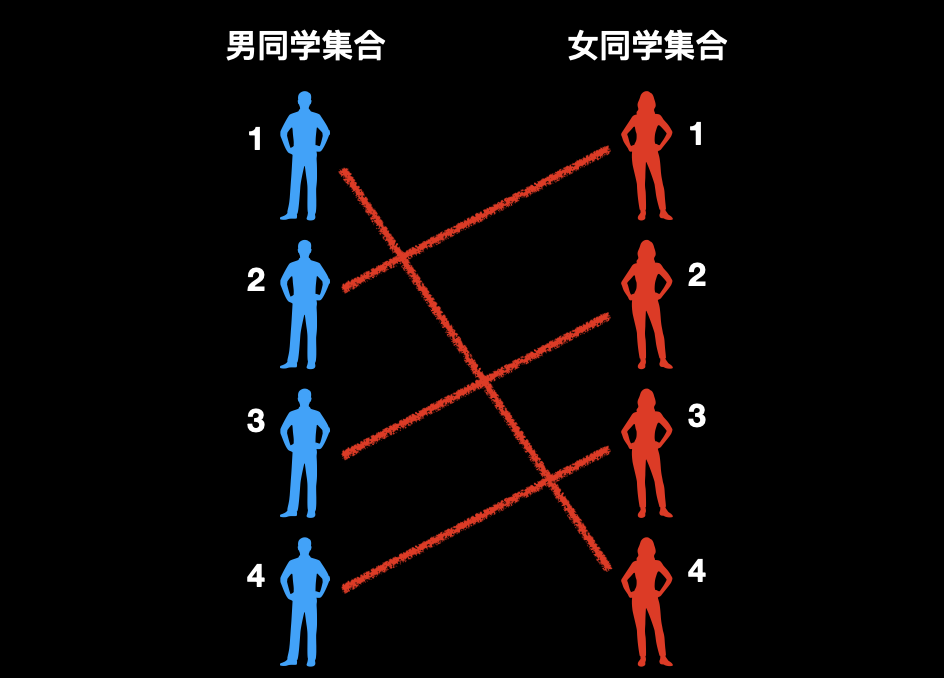
1、遍历到 1 号男同学，发现他和 2 号女同学具有好感，因此，我们先将他俩连一条红绳。

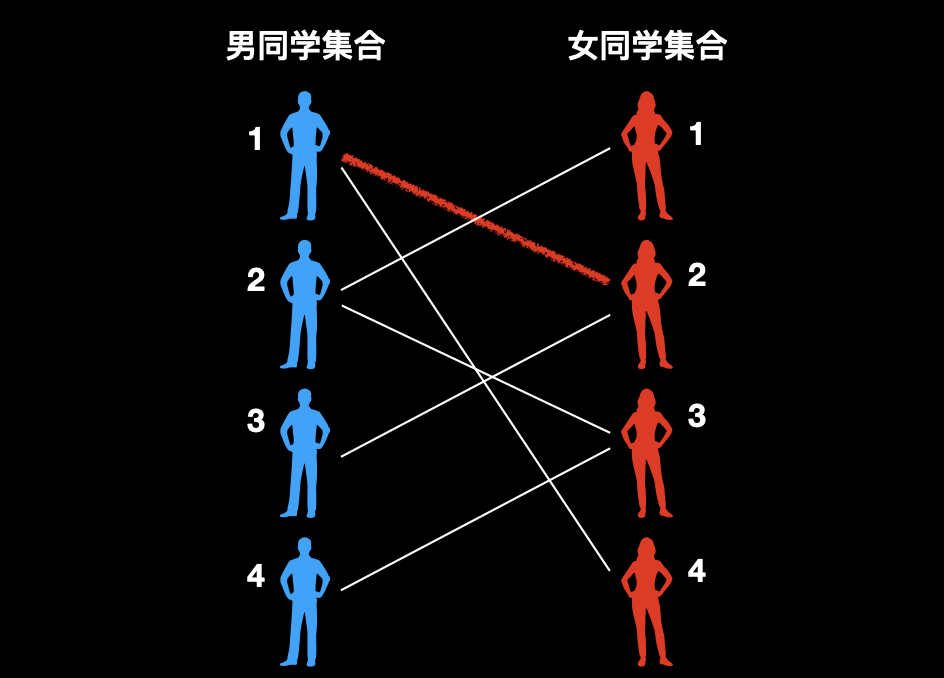
2、遍历到 2 号男同学，发现他和 1 号女同学具有好感，因此，他俩也可以连一条红绳。

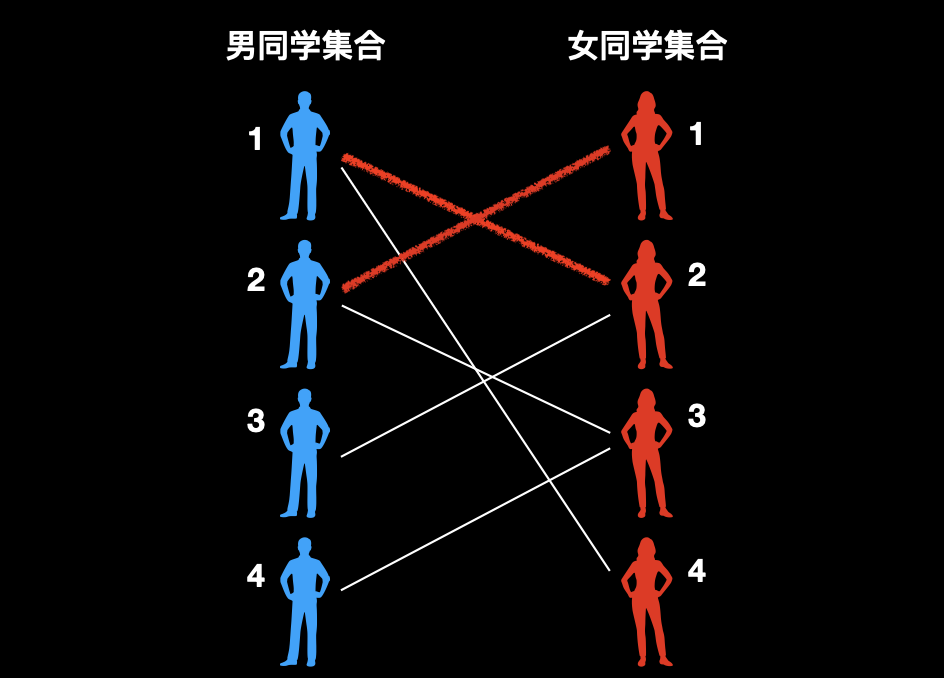
3、遍历到 3 号男同学，发现他和 2 号女同学具有好感，2 号女同学已经和 1 号男同学配对了。

此时关键来了，再看 1 号男同学发现他还和 4 号女同学具有好感，那么问题就简单了。我们给 1 号男和 2 号女一条绿绳子，让他们分开。

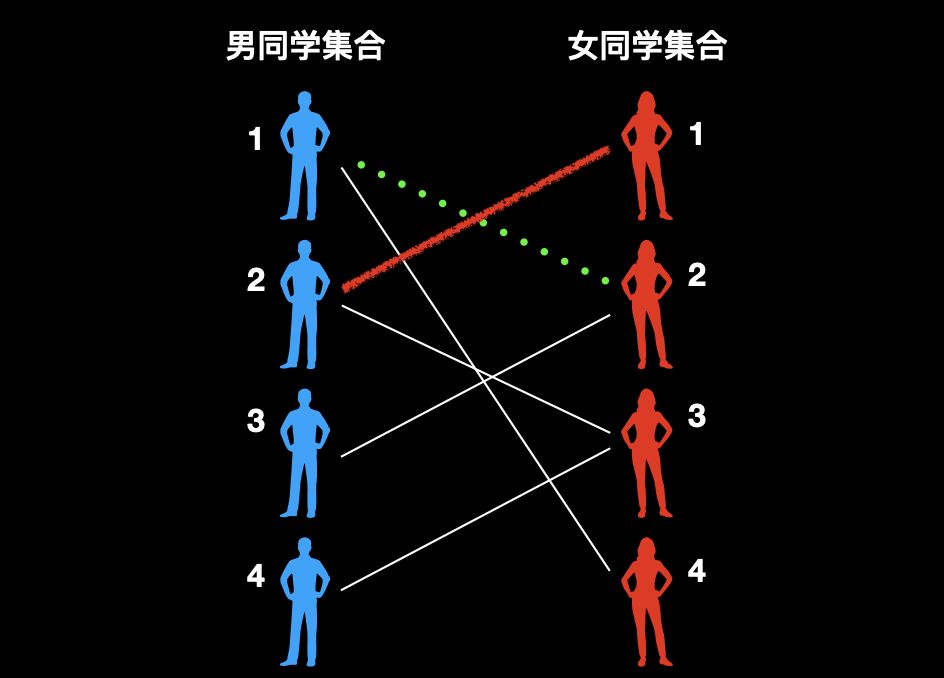
4、然后再把 1 号男和 4 号女配对，3 号男和 2 号女配对，皆大欢喜。

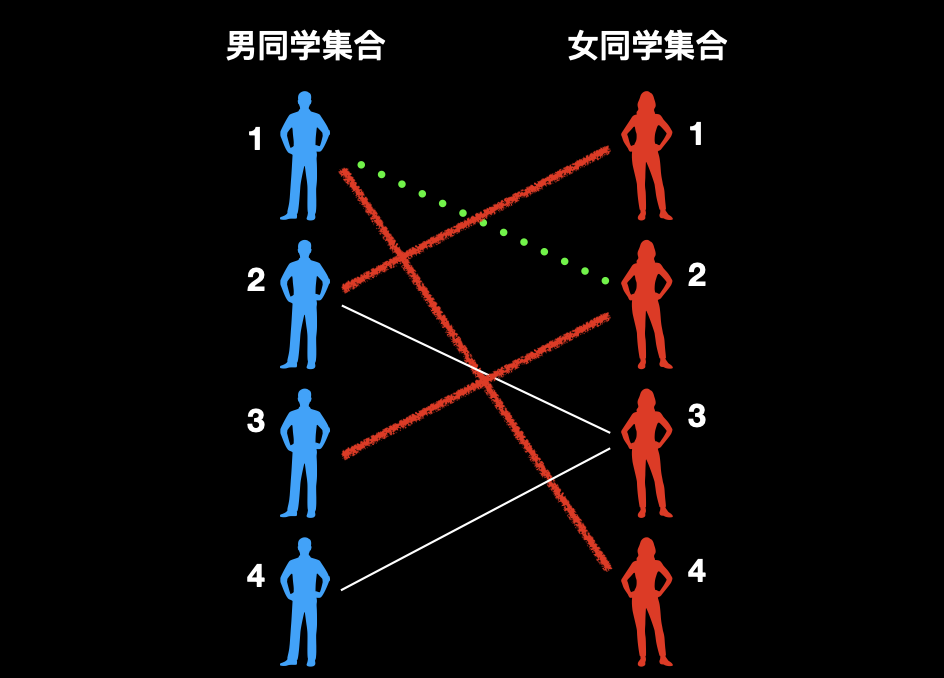
5、最后把 4 号男和 3 号女配对。获得最大匹配数，4 对。

# Code

	from collections import defaultdict
	# 读入数据 n1 是男同学数量，n2 是女同学数量
	n1, n2, m = map(int, input().split())
	# 保存具有好感度的同学
	edge = defaultdict(list)
	for _ in range(m):
	a, b = map(int, input().split())
	# 注意：此处因为我们后面只需要通过男同学寻找女同学
	# 所以不需要存女同学对应的男同学。
	edge[a].append(b)

	match = [0] * (n2 + 1) # 女同学匹配到了那个男同学

	# 给当前 boy 匹配个 girl
	def dfs(boy):
	# 与当前 boy 互有好感的所有 girl
	girls = edge[boy]
	for girl in girls:
	# 如果当前 gilr 未和当前 boy 匹配过
	if not status[girl]:
	# 记录这个 girl 已经被当前 boy 匹配了
	status[girl] = True
	# 核心代码如果当前 girl 没有对象直接把她给当前 boy
	# 如果有对象就 dfs 给他对象找新的 girl
	if not match[girl] or dfs(match[girl]):
	match[girl] = boy
	return True
	# 如果当前 boy 未能匹配任何妹子循环结束
	return False

	res = 0
	for i in range(1, n1 + 1):
	# 记录当前 boy 已经匹配过的 girl，避免 dfs 重复匹配相同 girl
	status = [0] * (n2 + 1)
	if dfs(i):
	res += 1
	print(res)

# 时间复杂度

从思路上分析，最外层循环我们遍历了每一个男同学，而匹配女同学的时候，最坏的情况就是被迫把所有的女同学都扫描一遍，所以总的时间复杂度为 O (NM)。