并查集是一种思路巧妙，代码很短的数据结构，也因此常常在算法题或者面试中出现。下面我们以一个模板题目作为示例，详细描述并查集的基本原理及使用。

# AcWing 836. 合并集合

一共有 n 个数，编号是 1∼n，最开始每个数各自在一个集合中。
现在要进行 m 个操作，操作共有两种：
M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；
输入格式
第一行输入整数 n 和 m。
接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b，都要输出一个结果，如果 a 和 b 在同一集合内，则输出 Yes，否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤105
输入样例
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例
Yes
No
Yes

# 题目描述

有 n 个数，编号 1~n。现在有两个操作：

M（merge）。合并两个数到一个集合中，如 M a b，则表示 a 和 b 合并到一个集合。
Q（query）。查询两个数是否在一个集合，如 Q a b，查询 a 和 b 是否在一个集合当中。

# 题目分析

分为常规思路和并查集两部分，读者可以对比这两种方法的不同，来初步理解并查集的作用。

# 常规思路

如果对于两个数，每个数初始都自己占用一个集合，那么合并两个数就将其中一个数的所属集合变为另外一个，但是这样做，在查询的时候则必须遍历两个数的所属集合，所以单次查询的时间复杂度是 O (n)。

# 使用并查集

# 概念

并查集，从名字中也可以看出来，这是一个专门负责合并与查询的数据结构。

在并查集中，使用多叉树的形式来维护所有的集合。使用根节点的编号来作为整个集合的编号，每个节点存储它的父节点，根节点存储它自己。用 p [x] 表示 x 的父节点编号。

白色数字：父节点编号；
绿色数字：节点本身的编号；

概念图

在这里，我们需要明确集合与节点是包含关系。

用集合的根节点编号表示一个集合。比如，也就是初始化之后，1 号节点因为它的节点编号和父节点编号相同，因此它就是一个集合的根节点，因为它的节点编号是 1，所以该集合的编号也是 1。
所以，后文所说的 "集合 1"，就是代表以 1 号节点为根节点的整个集合。在上图中，这个集合包含七个元素（未合并前）。

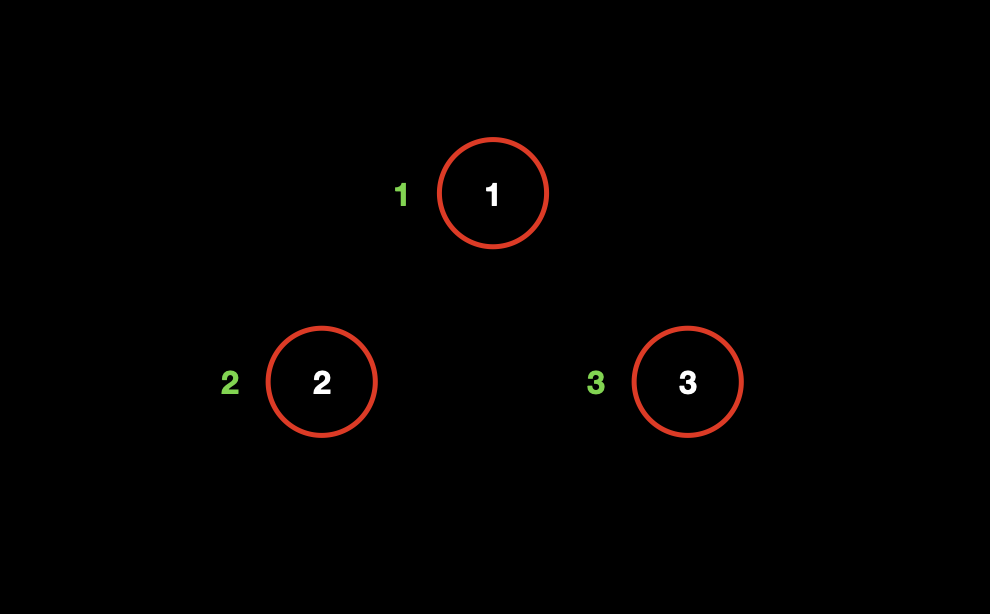
# 操作：初始化

为了方便后续的并和查的操作，我们在初始化阶段让每个节点都属于一个单独的集合，实现上就是节点编号等于它的父节点编号，如：节点 1 的父节点也是 1。

	// 初始化 n 个集合，每个集合 i 只有节点 i 一个元素。
	for (int i = 1; i <= n; i ++ )
	p[i] = i;

# 操作：合并

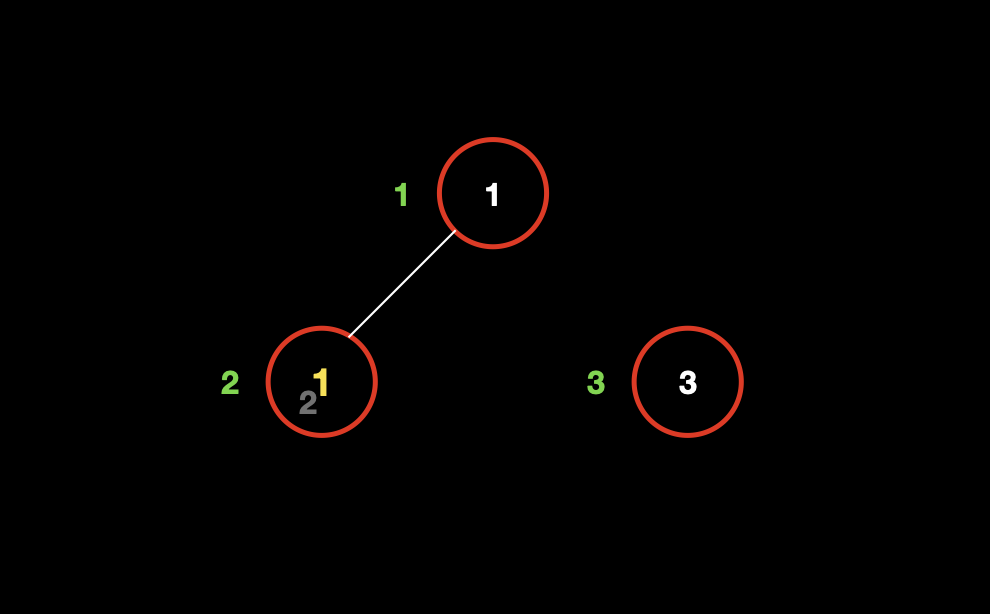
合并两个节点 a 和 b。直接将一个节点的所在集合指向另外一个节点的所在集合。

如下图，我们把节点 2 合并到节点 1，既，集合 2 的父节点编号变成集合 1 的节点编号。

	// 找到 a 和 b 的所属集合
	int x = find(a), y = find(b);
	// 下面两种方式均是把两个点合并到同一个集合
	p[x] = y; //x 的父节点是 y
	p[y] = x; //y 的父节点是 x

# 操作：查找

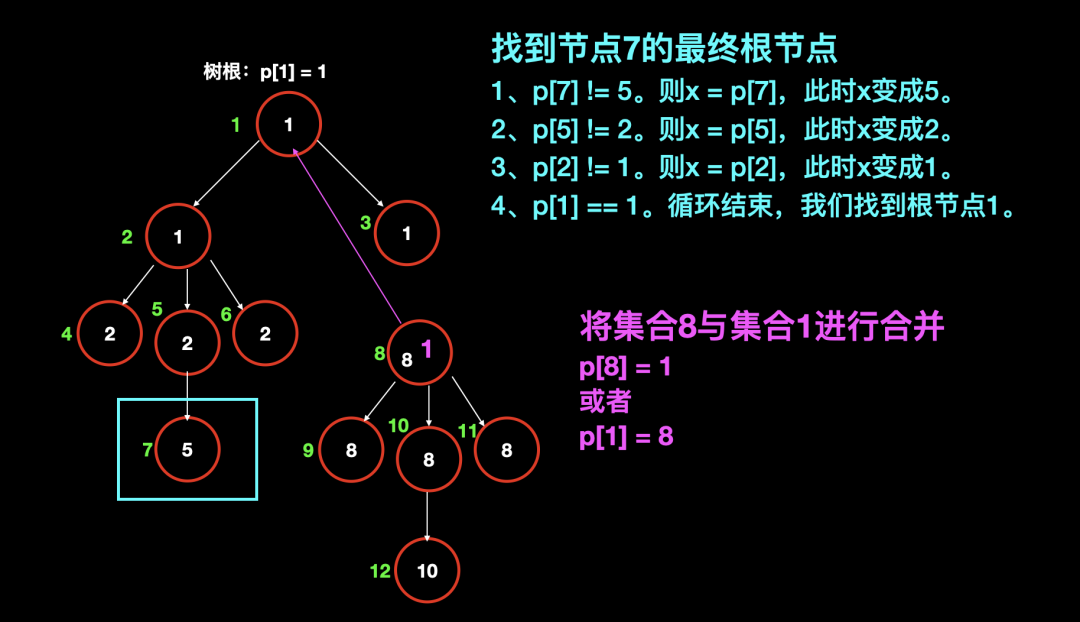
找到元素 x 属于哪个集合（也就是 find 函数）。我们沿着 x 的父节点一直向上搜索，直到找到 x 的最终根节点。

根据初始化的规则，我们可以直观的知道，判断一个点是不是最终根节点，实际上就是在看一个点的编号是否等于它的父节点的编号。用代码表示就是 (p[i] == i) 。
经过合并之后，节点的所属集合就会改变。
如图中节点 2 的所属集合本来是它自己，但是我们合并之后，把整个集合 2 合并到集合 1 上，所表现出来的现象就是原本节点 2 的父节点是它自己 (2) 表示它是集合 2 的最终根节点，合并之后节点 2 的父节点变成了节点 1，它的父节点不再是它自己，所以它也再属于集合 2。
那么，如何找到节点 2 合并后属于哪个集合呢？
我们只要沿着它的父节点向上找，直到找到最终根节点（参考概念图中天蓝色的文字描述部分）。
```
// 当循环停止之后，x就是所属的集合。
while (p[x] != x)  
    x = p[x];
```

# 优化：路径压缩

以概念图为例。

我们发现在查找这个操作上，我们要沿着父节点一点点的向上查找，直到找到最终根节点为止。

比如，找到节点 7 的所属集合，需要查找四次。这个查找次数和树的高度是成正比例的，也就是说所需要的时间复杂度是 log (n) 级别的。

而有一种优化方式，可以把这个复杂度优化到 O (1) 级别。在合并的时候，我们直接让所有的节点的父节点都指向所在集合的根节点。

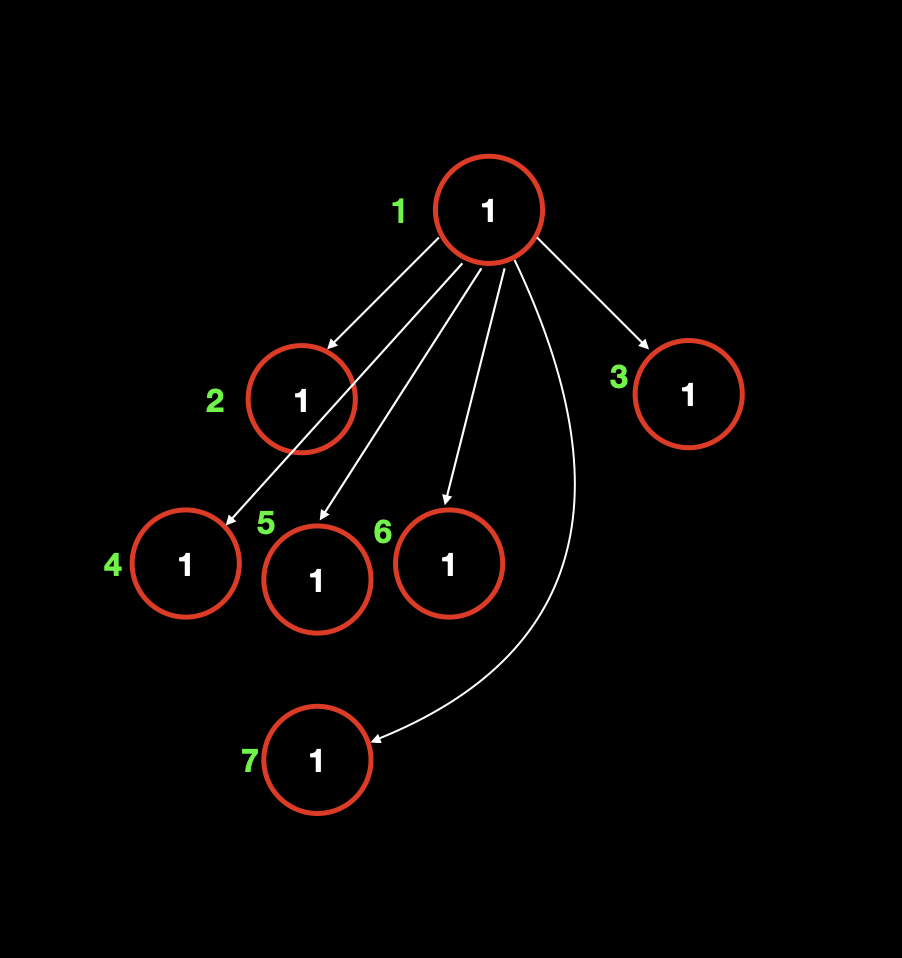
这种优化方式的好处也很明显，只需要向上找一次就可以知道某个元素属于哪个集合。

实现上，我们可以在查找操作的过程中，把对于非根节点把它指向它所在集合的根节点。

	int find(int x) {
	// 路径压缩
	if (p[x] != x) p[x] = find(p[x]);
	return p[x];
	}

# 维护额外信息

考虑这样一个问题：求某个集合的节点数量应该怎么办？

只需要多开一个数组 size [] 来记录每个集合中的节点数量。

初始化 size[] ，每个集合只有一个节点，既，根节点自己。只有集合合并的时候才会影响到一个集合的节点数量。所以在合并的时候，我们只要把两个集合的节点数量加一起就可以了。

比如： p[x]=y 该操作将 x 合并到集合 y 中，那么显然集合数量的变化就是 size[y] += size[x] 。

# Code

我们把上面分析的所有代码总结一下，就可以完成本题。

	#include <iostream>
	#include <cstring>

	using namespace std;

	const int N = 100010;
	int n, m;
	int p[N], size[N];

	// 查找
	int find(int x) {
	// 路径优化
	if (p[x] != x) p[x] = find(p[x]);
	return p[x];
	}

	// 合并
	int merge(int a, int b) {
	int x = find(a), y = find(b);
	p[x] = y;
	size[y] += size[x];
	}

	int main() {
	cin >> n >> m;
	// 初始化
	for (int i = 1; i <= n; i ++ ) p[i] = i, size[i] = 1;
	while (m -- ) {
	char t;
	int a, b;
	cin >> t >> a >> b;
	if (t == 'M') merge(a, b);
	else {
	int x = find(a), y = find(b);
	if (x != y) puts("No");
	else puts("Yes");
	}
	}
	return 0;
	}

END

并查集经典必会 AcWing算法基础课