# AcWing 291. 蒙德里安的梦想

求把 N×M 的棋盘分割成若干个 1×2 的的长方形，有多少种方案。
例如当 N=2，M=4 时，共有 5 种方案。当 N=2，M=3 时，共有 3 种方案。
如下图所示：
输入格式
输入包含多组测试用例。
每组测试用例占一行，包含两个整数 N 和 M。
当输入用例 N=0，M=0 时，表示输入终止，且该用例无需处理。
输出格式
每个测试用例输出一个结果，每个结果占一行。
数据范围
1 ≤ N, M ≤ 11
输入样例
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例
1
0
1
2
3
5
144
51205

# 题目分析

本题的题意可以根据 题目描述 中的示例理解。

从数据范围看， N 和 M 的最大值都只有 11 ，这就提示了我们本题可以使用 状态压缩动态规划 来做。

在摆放方块的时候，一定要注意一个核心点：先横着摆，再竖着摆。这是因为当把横着的摆放完之后，剩下竖着的位置是确定的。所以本题求的总方案数，就可以转化为所有只放横着小方块的合法方案数。

如何判断出当前方案是否合法呢？
只要剩余的位置能用竖着的小方块填满，就说明方案合法。那么当横着摆放完之后，按列来看，只要每一列内部连续空着的小方块是偶数个数，就说明可以竖着填满。

以 N=2，M=3 为例进行说明。

方案 1.
先横着摆放。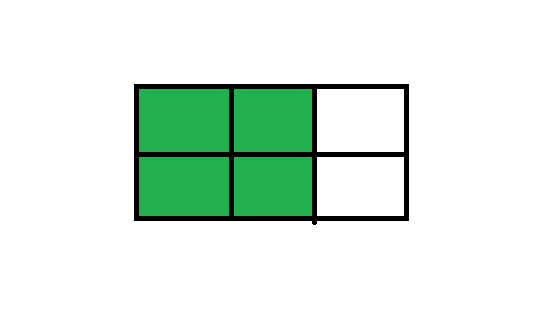

此时，已经不能再横着放，开始竖着放，考虑每列的剩余空间，
第一列无剩余空间，第二列无剩余空间，第三列剩余空间为偶数，因此可以用竖着的小方块填充满所有格子，方案合法。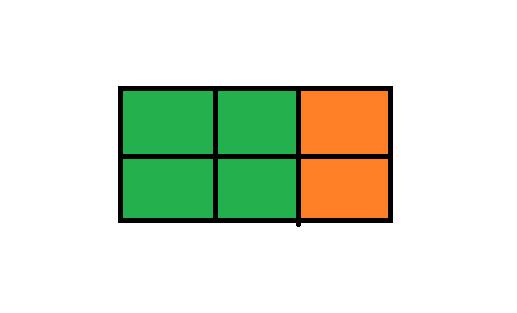

方案 2.
先横着摆放，填充满后两列。再考虑剩下的第一列有偶数个的剩余空间，所以可以填充满所有格子，方案合法。

方案 3.
先横着摆放（横着摆放 0 个方块）。再考虑剩下的每一列，剩下三列都有偶数个空余位置，因此都可以用竖着的小方块填充满，方案合法。

# 状态压缩动态规划

状态压缩：使用二进制来表示状态，但是存储的时候使用十进制来存。

状态定义：用 f(i, j) 表示已经将前 i-1 列及其之前所有列摆放好，且从第 i-1 列伸出到第 i 列的状态为 j 的所有方案数。

# 举例

当 $i=2, j={(1010)}_2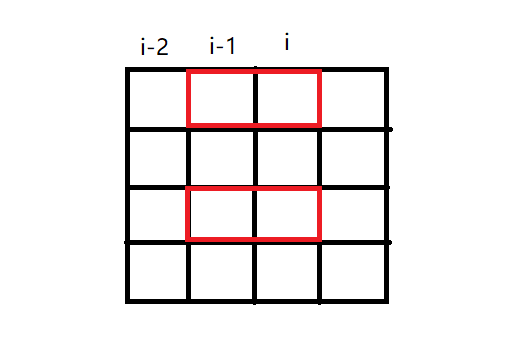$ 时候，此时状态如下：

根据我们对状态的定义，上述的状态用自然语言描述为：此时，第 i-1 列及其前面的所有列已经摆放好了，且 i-1 列中，第 1 行和第 3 行横着的方块延伸到了第 i 列，用二进制表示状态 j 为 1010 。

# 状态转移 (集合划分)

观察对于状态的定义，我们可以发现由 i-1 到 i 的状态已经是确定的，也就是我们状态定义中的 j 。

但是由 i-2 到 i-1 的状态是不确定的。更明确点说，我们的状态定义 f(i, j) 中只定义了 i-1 列及其之前列摆放好了，但是具体是如何摆放的并没有确定。所以我们可以枚举第 i-2 列到第 i-1 的状态 k 。那么我们惊奇的发现根据状态定义， i-2 到 i-1 的且状态为 k 的方案数不就是 f (i-1, k) 嘛。把所有枚举出来的 f(i-1, k) 都累加起来就构成了 f(i, j) 。

那么最后的答案是什么呢？

其实就是 f(m, 0) ，我们把这个状态带入到定义中，它表示前 m-1 列都已经摆放好啦，并且延伸到 m 列的行数是 0。这个状态恰好就是摆满 N * M 大小棋盘的所有方案数。

转换中需要注意方案是否合法
由于从 f(i-1, k) 转换到 f(i, j) 能否构成一个合法方案是不确定的。所以现在需要想一下，什么情况下它俩无法构成一个合法方案。

根据状态定义 f(i, j) ，在计算当前状态 i 的时候，前面 i-1 列及其前面列的横向方块是已经摆放好的，也就是说前 i-1 列剩下的空间必须能被竖着的小方块完全填充，也就是每列剩下的空间必须全是偶数。
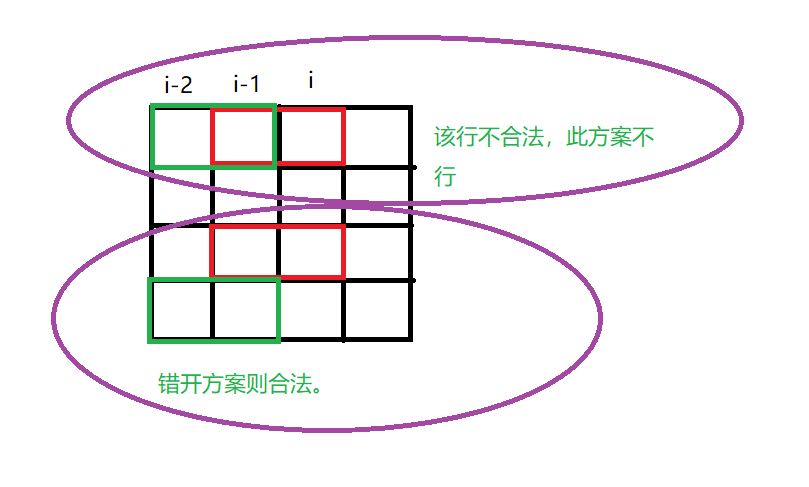
第 i-1 列和第 i 列是可能出现重复的。如果从 i-1 行延伸到了第 i 行就说明 i-1 行已经被占用了，那么 i-1 行就一定不能由 i-2 行延伸过来。而 k 和 j 的二进制表示中，如果是 1 就说明这一行是延伸的，所以 k 和 j 的同一行是不可以存在两个 1 的。也就是说必须满足 k & j == 0 才可以转移。

# Code

	def dp(n, m):
	N = 12
	M = 1 << N
	f = [[0] * (M) for _ in range(N)]
	# 初始化表示从 - 1 列伸出到第 0 列且全摆好的方案
	# 但是没有第 - 1 列所以这里表示第 0 列竖着摆
	# 参考例子 n=2、m=3 时候的方案 3
	f[0][0] = 1
	# st 存储所有的状态中能构成合法方案的
	st = [0] * M
	# state 存储与状态 j 不冲突的状态 k
	state = [[] for _ in range(M)]

	# 预处理 1 对应分析中的无法构成合法方案的情况 1
	# 状态 i 下是否会有连续奇数 0 的情况
	# 枚举状态 i
	for i in range(1 << n):
	# 举例：如果第 j 列此时为 100101 则结果是不合法
	# 当第一次遍历是 1 cnt0 合法第二三次是 0 cnt 变成 2 是偶数合法
	# 第四次遍历是 1 cnt 变成 0 第五次 cnt 变成 1 第六次是 1 判断 cnt 不合法
	cnt = 0 # 记录连续 0 的个数
	is_valid = True
	# 从上到下遍历列。
	for j in range(n):
	# i >> j 表示 i 二进制的第 j 位， &1 表示该位是不是 1
	if i >> j & 1:
	# 如果连续 0 是奇数说明没法竖着填充满
	if cnt & 1:
	is_valid = False
	break
	cnt = 0
	# 如果不是 1 统计连续 0 的个数
	else:
	cnt += 1
	# 判断最后一段 0 是否合法
	# 避免遗漏形如 000 的状态。
	if cnt & 1:
	is_valid = False
	st[i] = is_valid

	# 预处理 2 对应分析中的无法构成合法方案的情况 2
	# 既 i-2 延伸到了 i-1 此时 i-1 就无法在延伸到 i
	# 枚举第 i 列所有状态 j
	for j in range(1 << n):
	# 枚举 i-1 列所有状态 k
	for k in range(1 << n):
	# j & k 分析中已经有表述。
	# st 表示该列是否有连续个 0
	# 而在这里我们除了要考虑 i-1 延伸到 i 还要考虑 i-2 延伸到 i-1
	# 因为 i-2 如果延伸到 i-1 那么 i-1 也要横着放格子
	# 比如 i-2 延伸到 i-1 状态是 01000
	# i-1 延伸到 i 状态是 10010
	# 那么 i-1 横着放格子的行自然是 j \| k = 01000 \| 10010 = 11010
	if ((j & k) == 0) and st[j \| k] == True:
	# 存储与状态 j 不冲突的状态 k
	state[j].append(k)

	# 枚举每一列
	for i in range(1, m + 1):
	# 枚举状态 j
	for j in range(1 << n):
	# 枚举可以与 j 构成合法方案的状态 k
	for k in state[j]:
	f[i][j] += f[i - 1][k]
	print(f[m][0])

	while 1:
	n, m = list(map(int, input().split()))
	if n == 0 and m == 0:
	break
	dp(n, m)