# AcWing 895. 最长上升子序列

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数 N。
第二行包含 N 个整数，表示完整序列。
输出格式
输出一个整数，表示最大长度。
数据范围
请重点关注一下此处的数据范围
1 ≤ N ≤ 1000 ，
${-10^9}$ ≤ 数列中的数 ≤ ${ 10^9 }$ .
输入样例
7
3 1 2 1 8 5 6
输出样例
4

# 题目分析

最长上升子序列 是 最经典、最基础、最简单 的动态规划题目。

# 先简单看一下题意

给出一个长度为 N 的数列 nums ，从该数列中找出数值严格单调递增的最长子序列。

子序列：从 前往后扫 描数列，过程中 任意选取 若干元素，组成的新序列。

从前往后扫描给定样例 [3, 1, 2, 1, 8, 5, 6] ，找到其中严格单调递增的最长子序列，很容易发现是 [1, 2, 5, 6] ，总长度是 4 ，所以最终答案就是 4 。

# 动态规划

在前面的文章中，我们已经了解到动态规划有两个基本步骤：状态定义和状态转移。

在状态定义部分又分为 集合 和 集合的属性 两个概念。而状态转移则是考虑 集合如何划分 。

# 本题思路

# 状态定义

用 f(i) 表示状态。根据最终目标 严格单调递增的最长子序列 ，划分状态集合为 所有以第 i 个数结尾的上升子序列 ，而状态属性则是 集合中子序列长度的max 。

例如：
状态 f(4) 表示的集合是以 nums[4] 为结尾的所有上升子序列。包括 [(3,8),(1,8),(2,8),(1,2,8)] ，状态属性表示为 这些子序列长度的最大值 ，也就是 3 ，所以有 f[4]=3 。

理解状态定义之后，发现动态数组 f 中存储的就是以 nums 中每个元素结尾的最长上升子序列，那么 f 数组中的最大值就是最后的最长上升子序列。

# 状态转移

在考虑集合如何划分的部分的时候，我们依赖一个重要性质对于状态 f(i) ，它的最长上升子序列的最后一个元素一定是 nums[i] ，但是 f(i) 的 倒数第二个元素nums[j] ，是不确定的，因此我们可以通过 f(i) 倒数第二个元素来划分集合中的子序列。

枚举出所有可能成为 倒数第二个元素 的所有元素，也就是数列 nums[0, i] 的所有元素。他们都有可能成为 倒数第二个元素nums[j] 。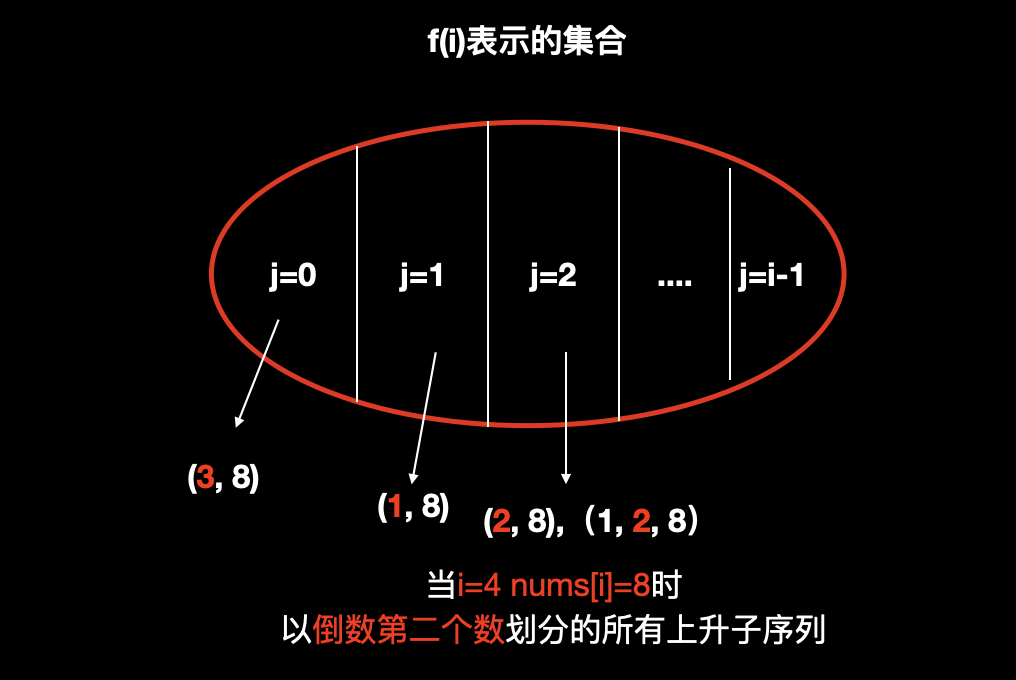

根据状态的定义， f(j) 表示的就是 以nums[j]结尾的最长上升子序列 。那我们考虑以下两种情况完成状态转移：

如果当前有 nums[j]<nums[i] ，我们就很容易推出状态转移 f(i)=f(j)+1 ，表示含义也就是当前元素 nums[i] 大于上一个元素 nums[j] 的情况下，当前最长上升子序列就等于它前一个元素的最长上升子序列的长度加一。
如果当前有 nums[j]>=nums[i] ，状态转移就是 f(i)=f(j) ，表示的含义是由前一个元素到当前元素不再是数值上升的，因此当前元素的状态就是前一元素的状态。

# Code

	n = int(input())
	nums = [int(num) for num in input().split()]
	# 初始化状态数组每个元素本身也视为一个长度为 1 的上升子序列
	f = [1] * (n + 1)
	# 枚举数列中的每一个数
	for i in range(n):
	# 枚举可能的倒数第二个数 (0~i-1)
	for j in range(i):
	if nums[j] < nums[i]:
	f[i] = max(f[j] + 1, f[i])
	# f 数组中存储了以每个元素为结尾的最长上升子序列
	print(max(f))

从代码中不难看出 (两层循环) 动态规划的时间复杂度是 ${O(n^2)}$ 。这在本题的数据范围 1 ≤ N ≤ 1000 是可以的，因为 ${10^6}$ 是不会超时的，但是如果这个数据范围增加到 1 ≤ N ≤ 100000 ，那么使用 ${O(n^2)}$ 复杂度的算法就会超时。所以我们需要一个更快的算法。

# 提高了数据范围

将题目的数据范围提升到 1 ≤ N ≤ 100000 。

# 动态规划中的冗余操作

我们注意到在最长上升子序列中，从长度为 1 的子序列开始算起。那么示例中第一个上升子序列是 (3) ，第二个是 (1) 。

因为最终目的是求 整个数列(nums) 的最长上升子序列，那么后续的子序列计算中就可以忽略掉第一个上升子序列 (3) ，这是因为第二个数字 1 比 3 更小，所以最终上升子序列的后续元素，如果能放在 1 后面的，一定也能放在 3 后面。

根据上面的分析，我们可以推出一个基本结论：如果保存 所有长度的上升子序列的结尾值 ，那么 随着长度的增加，结尾值也一定是递增的 。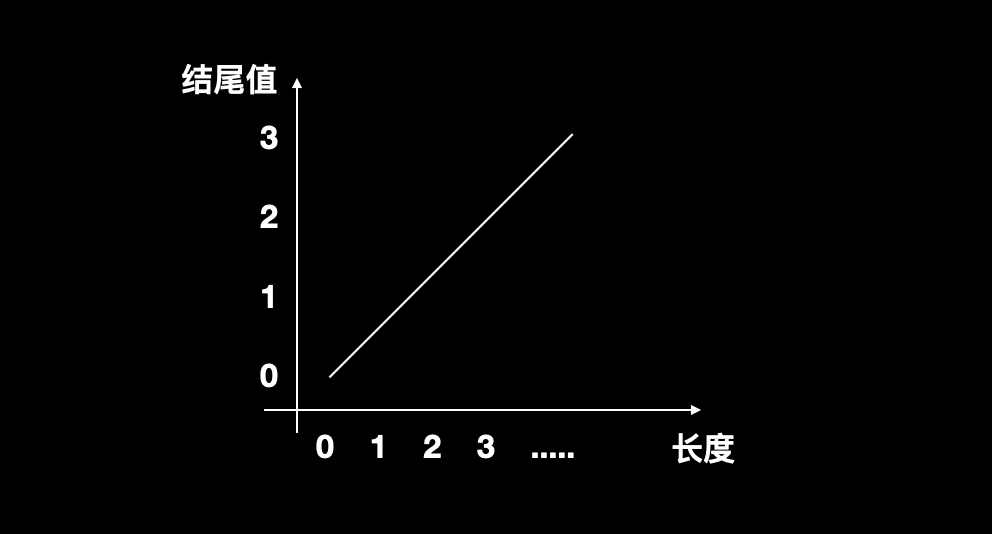

如何证明这个结论呢？

可以使用反证法。假设长度为 5 的最长上升子序列的结尾值是 7 ，而长度为 6 的最长上升子序列的结尾值比 7 更小，则会不符合定义。因为我们保存的长度为 5 的上升子序列的结尾值 7 已经是此时的最小值，如果长度增加了 1 最小值反而小的话，说明子序列不满足严格递增这一条件。因此保存结尾最小值的序列一定也是严格递增的。

所以我们可以用二分法来构建这个序列 q 。

以示例 [3, 1, 2, 1, 8, 5, 6] 举例：

扫描整个数列，第一个元素是 3 ，此时长度为 1 ，说明长度为 1 的最长上升子序列结尾值为 3 ，因此 q[1]=3 ;
扫描到第二个元素 1 ，用二分找到它在 q 中的位置（即保证 q 是严格递增序列）。我们发现这个位置就是此时 3 所在位置，所以 q[1]=1 ;
扫描到第三个元素 2 ，发现它比此时的结尾值大，说明最长上升子序列的长度又可以增加了，因此把 2 直接放在 q[2]=2 ;
扫描到第四个元素 1 ，放在 q[1]=1 ;
扫描到第五个元素 8 ，最长上升子序列的长度增加，把 8 直接放在 q[3]=8 ;
扫描到第六个元素 5 ，此时 q=[1,2,8] ，二分出 5 的位置，也就是现在 8 的所在，替换掉；
扫描到第七个元素 6 ，此时 q=[1,2,5] ，发现 6 比结尾值更大，因此最长上升子序列的长度增加，并且 q[4]=6 ;
最终，我们构建一个数组 q ，其中保存这不同长度对应的最长上升子序列的结尾值 q=[1,2,5,6] 。

# Code

	n = int(input())
	nums = list(map(int, input().split()))
	q = [0] * (n + 1)

	maxx = 0 # 存储最终的最长上升子序列长度
	for i in range(n):
	# 二分上下界为 0 和最终长度
	l, r = 0, maxx
	while l < r:
	mid = l + r + 1 >> 1
	# 当前值大于 q 中值，搜索右面 [mid, r]
	if q[mid] < nums[i]:
	l = mid
	else:
	r = mid - 1
	q[r + 1] = nums[i] # 把当前值放到 q 中
	# 如果当前值的位置比最终长度还大，
	# 说明最终值可以增长。
	if r + 1 > maxx:
	maxx += 1
	print(q) # [0, 1, 2, 5, 6, 0, 0, 0]
	print(maxx)

经典必会基础模板题最长上升子序列 AcWing算法基础课

# AcWing 895. 最长上升子序列

# 题目分析

# 先简单看一下题意

# 动态规划

# 本题思路

# 状态定义

# 状态转移

# Code

# 提高了数据范围

# 动态规划中的冗余操作

# Code

LeetCode 373. 查找和最小的K对数字

AcWing 291. 蒙德里安的梦想