# 前置文章

Floyd 算法简单入门

# AcWing 344. 观光之旅

给定一张无向图，求图中一个至少包含 3 个点的环，环上的节点不重复，并且环上的边的长度之和最小。
该问题称为无向图的最小环问题。
你需要输出最小环的方案，若最小环不唯一，输出任意一个均可。
输入格式
第一行包含两个整数 N 和 M，表示无向图有 N 个点，M 条边。
接下来 M 行，每行包含三个整数 u，v，l，表示点 u 和点 v 之间有一条边，边长为 l。
输出格式
输出占一行，包含最小环的所有节点（按顺序输出），如果不存在则输出 No solution.。
数据范围
1≤N≤100,
1≤M≤10000,
1≤l<500
输入样例
5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20
输出样例
1 3 5 2

# 题目描述

给出一张无向图，问图中所有至少包含三个点的环中，环上的边的长度总和最小是多少。

# 题目分析

本题如果是求两个点中的环长度最小非常简单，两个环其实就是边，因为是无向图，所以就是求最小的边，但是本题要求了至少三个边组成的环，问题就变得麻烦了起来。

# 关于 “环上的节点不重复”

题目中给出了一个条件 “环上的节点不重复”，说明，每个环中任何一个节点都只存在一次。但是这个条件，我们仔细思考一下，会发现即便环上的节点是重复的对最终结果也没有影响，因为根据数据范围，所有的边的权重都是大于一的，那么，我们去除重复的边一定可以使整个环的权重变小。

如下图，虽然绿色边使那个点被经过了两次，但是因为边的长度一定大于一，所以去掉边后依旧是一个环，并且环的权重更小。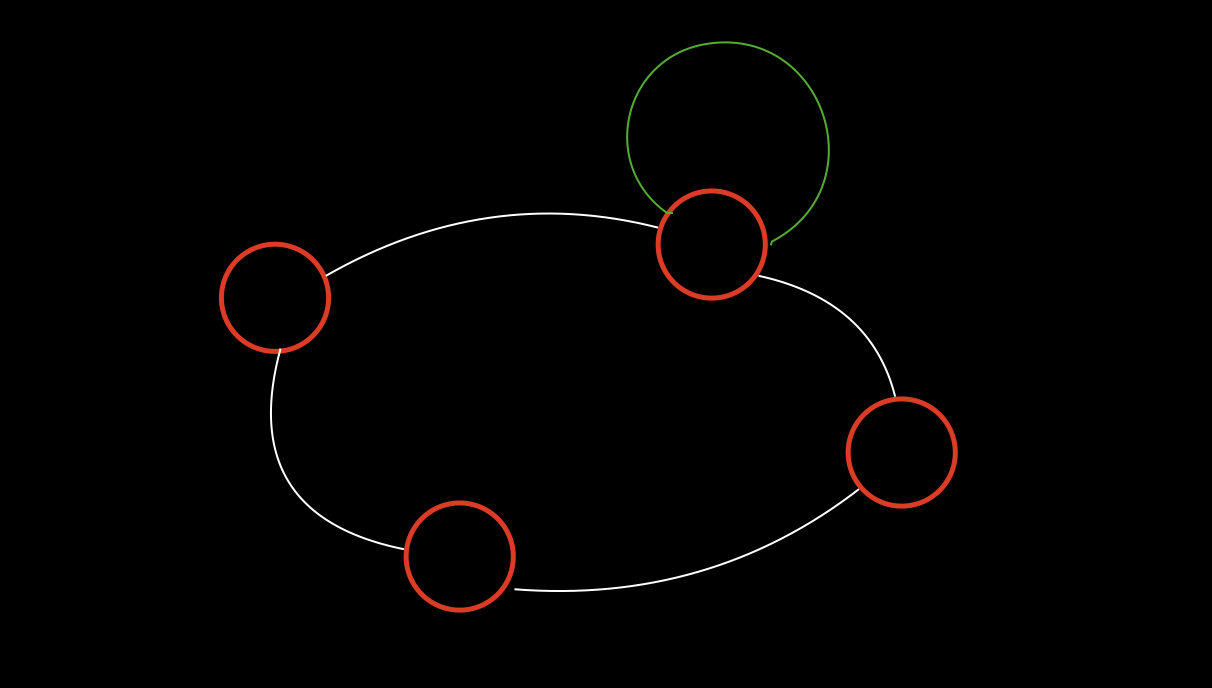

# 动态规划的思路

因为 floyd 的思路本质上是动态规划，所以我们也按照动态规划的思路从集合的角度来分析本题。

首先，我们要想一种划分方式，将所有的环进行分类。一般的动态规划中，我们经常以最后一个状态是由哪个状态转移而来进行划分。

在本题中，我们继承这种思路，把所有的环，根据编号最大的点进行划分集合。

注意这种划分方式的好处是：

可以不重不漏的包含所有的环；
划分好后，我们求出每一个集合中的最小值，然后再从每一个集合的最小值中，找出最终的最小值，就是结果。

那么，每一集合中的最小值怎么求呢？

可以从 floyd 的求解过程中找到答案。

	for (int k = 0; k < n; k ++ )
	// 此处已经求出了只经过 (1~k-1) 这些点的最短路径 d [i][j]
	for (int i = 0; i < n; i ++ )
	for (int j = 0; j < n; j ++ )
	d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

我们知道 floyd 算法的最大作用就是可以求出有边数限制的最短路。其中边数限制指的就是以上代码中的第一重循环 k ，也就是说当循环到 k 的时候，就已经知道了，所有从 i 到 j（d [i,j]），只经过 1~k-1 这些点的最短路径。

所以，我们在这个位置（上面代码注释的位置）就可以求出第 k 类（也就是编号最大为 k 的集合中的环的最小权重）。

那怎么求呢？我们可以发现，这个集合（k 为环中最大点的编号，下面简称集合 k）中的环，全部是如下形式：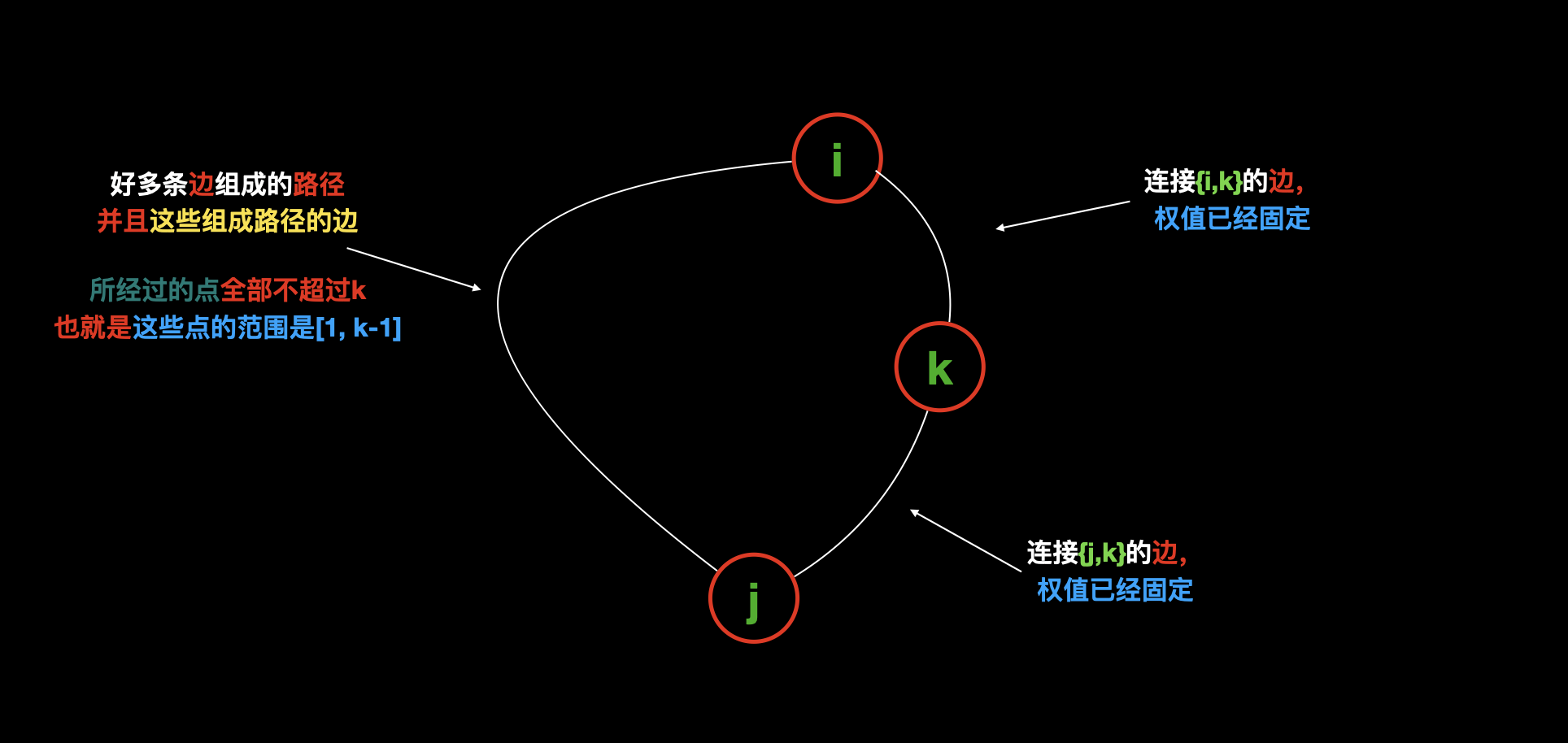

根据图中的分析，我们知道了集合 k 中的环，全部是由三部分组成：

i 到 k 的距离是固定的，记作 w[i][k] ；
j 到 k 的距离也是固定的，记作 w[j][k] ；
所有 i 到 j，且经过的最大点编号小于等于 k-1 的最短距离，在第一重循环到 k 的时候已经知道了。记作 d[i][j] 。。

那么最终集合 k 的最小值就是：枚举 i 和 j，求 min({d[i][j]}) + w[i][k] + w[j][k] 。

那么最终所有集合最小值就是：枚举所有的 集合k ，也即是 集合1~n ，然后求他们的一个最小值就行了。

# Code

本题在实现上还有一个难点，既：最后题目要求输出包含最小环的所有节点（按顺序输出）。

因此，我们还需要存储一下节点的转移路线。

考虑状态转移的部分： d[i][j]=d[i][k]+d[k][j] ，其中边 {i,j} 被 k 分成两部分，当前的 d[i][j] 由中间点 k 转移而来，因此在每次转移的时候记录这个点 k，记作 pos[i][j]=k 。

有了 pos 数组，求环的路径的时候就可以通过递归来遍历出整条环上的路径。

	#include <iostream>
	#include <cstring>
	#include <algorithm>

	using namespace std;

	const int N = 110, INF = 0x3f3f3f3f;

	int n, m;
	// 数组含义见分析
	int w[N][N], d[N][N];
	int pos[N][N];
	//path 表示当前最小环的路径 cnt 表示对应路径的点数量
	int path[N], cnt;

	void get_path(int i, int j) {
	// 如果 ij 没被更新过说明没有中间点
	// 它俩就组成一条边
	if (pos[i][j] == 0) return ;
	int k = pos[i][j]; // 取出更新它的点 k
	get_path(i, k); // 先从 i 走到它俩的中间点 k
	path[cnt ++ ] = k; // 把 k 加上
	get_path(k, j); // 再从 k 走到 j

	}

	int main() {
	cin >> n >> m;
	// 初始化两点间的距离
	memset(w, 0x3f, sizeof w);
	for (int i = 1; i <= n; i ++ ) w[i][i] = 0;

	while (m -- ) {
	int a, b, c;
	cin >> a >> b >> c;
	// 无向图建立双向边以及重边的话取最小值
	w[a][b] = w[b][a] = min(w[a][b], c);
	}
	int res = INF;
	memcpy(d, w, sizeof d);
	//floyd 算法
	for (int k = 1; k <= n; k ++ ) {
	// 在这个位置枚举每个集合的最小值并更新最终答案
	// 注意 i 和 j 的范围都是 1~k-1
	// 但是因为是双向图 w [i][j] == w [j][i]
	// 因此 j 枚举一半就行所以我们选择从 i+1 枚举 j
	for (int i = 1; i < k; i ++ ) {
	for (int j = i + 1; j < k; j ++ ) {
	// 判断当前环是否能更新结果不转 LL 会爆 int
	if ((long long)d[i][j] + w[i][k] + w[k][j] < res) {
	res = d[i][j] + w[i][k] + w[k][j];
	// 当前环是最小环那把当前环的路线更新到 path 数组
	cnt = 0;
	path[cnt ++ ] = k; // 先放点 k
	path[cnt ++ ] = i; // 从 k 走到 i 再放点 i
	get_path(i, j); // 路径 i 到 j 有很多点递归放 i~j 最短距离的所有点
	path[cnt ++ ] = j; // 最后放 j
	}
	}
	}
	for (int i = 1; i <= n; i ++ ) {
	for (int j = 1; j <= n; j ++ ) {
	if (d[i][j] > d[i][k] + d[k][j]) {
	d[i][j] = d[i][k] + d[k][j];
	// 记录当前 {i,j} 最小距离是由哪个 k 转换而来的
	pos[i][j] = k;
	}
	}
	}
	}
	if (res == INF) puts("No solution.");
	else {
	for (int i = 0; i < cnt; i ++ ) cout << path[i] << ' ';
	}
	}

END