# LeetCode 913. 猫和老鼠

两位玩家分别扮演猫和老鼠，在一张 无向 图上进行游戏，两人轮流行动。

图的形式是：graph [a] 是一个列表，由满足  ab 是图中的一条边的所有节点 b 组成。

老鼠从节点 1 开始，第一个出发；猫从节点 2 开始，第二个出发。在节点 0 处有一个洞。

在每个玩家的行动中，他们 必须 沿着图中与所在当前位置连通的一条边移动。例如，如果老鼠在节点 1 ，那么它必须移动到 graph [1] 中的任一节点。

此外，猫无法移动到洞中（节点 0）。

然后，游戏在出现以下三种情形之一时结束：

• 如果猫和老鼠出现在同一个节点，猫获胜。
• 如果老鼠到达洞中，老鼠获胜。
• 如果某一位置重复出现（即，玩家的位置和移动顺序都与上一次行动相同），游戏平局。

给你一张图 graph ，并假设两位玩家都都以最佳状态参与游戏：

• 如果老鼠获胜，则返回  1；
• 如果猫获胜，则返回 2；
• 如果平局，则返回 0 。

示例 1

输入：graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
输出：0

示例 2

输入：graph = [[1,3],[0],[3],[0,2]]
输出：1

提示

• 3 <= graph.length <= 50
• 1 <= graph[i].length < graph.length
• 0 <= graph[i][j] < graph.length
• graph[i][j] != i
• graph [i] 互不相同
• 猫和老鼠在游戏中总是移动

# 题目分析

汤姆和杰瑞的故事。

先来简单的看一下题意：

• 在一个无向图上有若干节点，并给出了连通的边。老鼠和猫咪沿着图的边行动。老鼠先走，猫咪再追。
• 一个非常重要的前提是，无论老鼠还是猫咪每次都会做出最佳选择。
• 有三种最终结果：
  • 猫咪胜利。即，在老鼠走到点 0 之前，猫咪和老鼠走到了同一个点。
  • 老鼠胜利。即，老鼠顺利走到了点 0。
  • 双方平局。即，老鼠和猫咪的位置和移动顺序都与上一次相同。

前面两种结果，猫或鼠赢都比较好理解，平局的情况我们可以根据 示例1 理解。

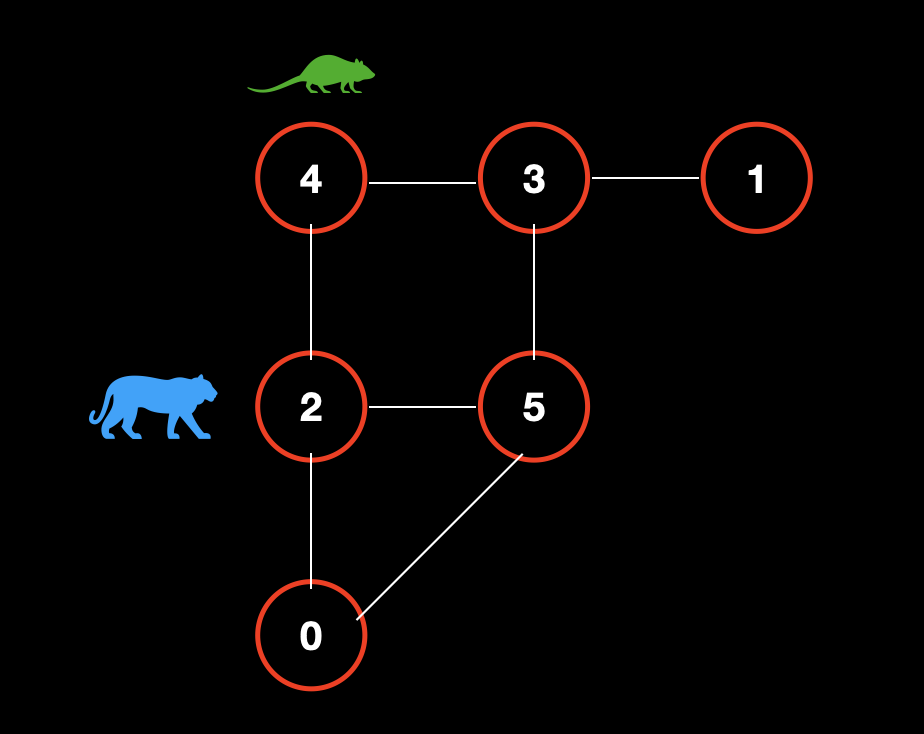
# 示例 1 分析

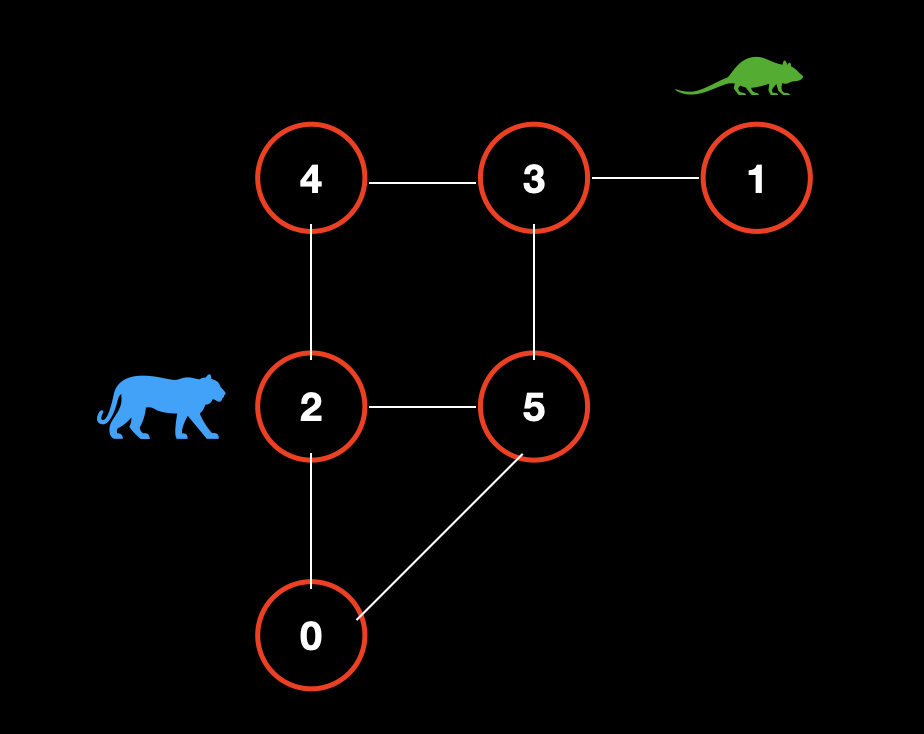
1. 初始状态。在初始的时候，老鼠必定在点 1，猫咪必定在点 2。
   

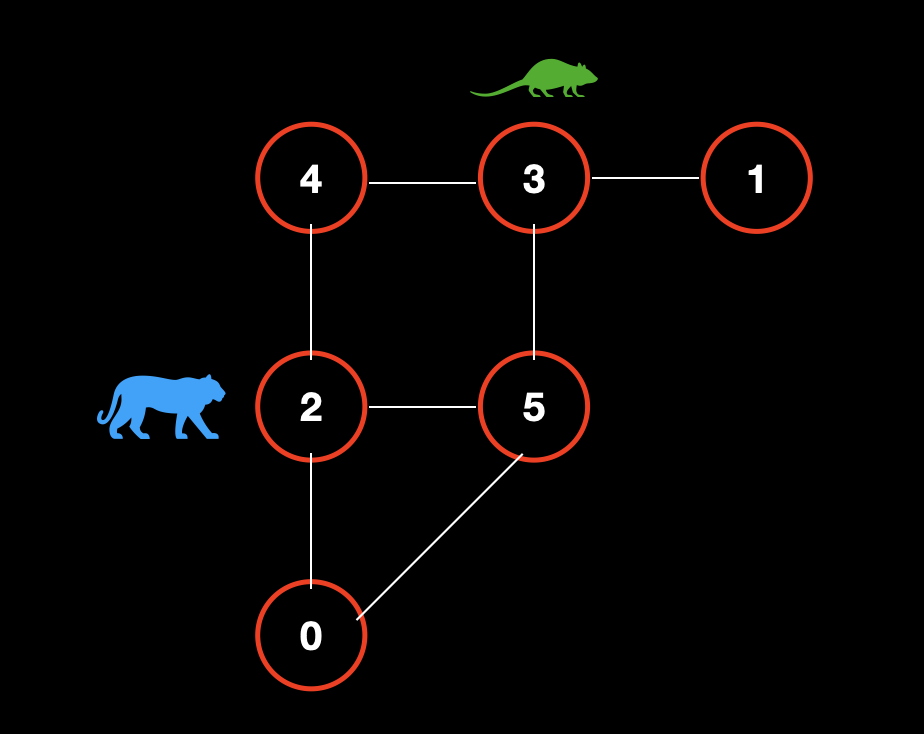
2. 老鼠走。老鼠在点 1，它先走，并且只能走到点 3。
   

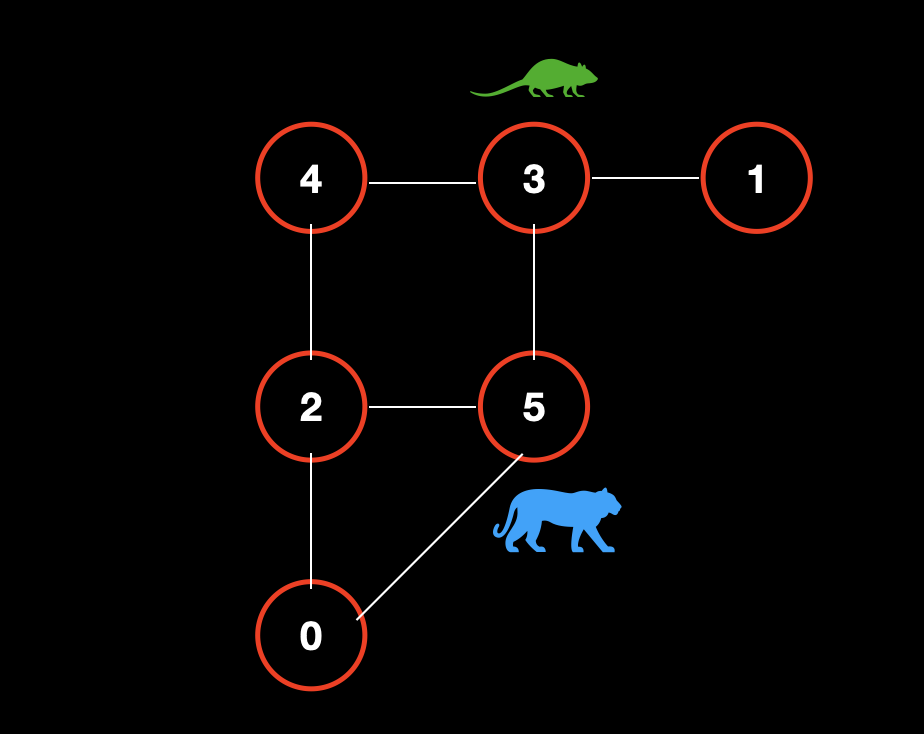
3. 猫咪走。此时，猫咪在点 2，它看似有两种选择：点 4 和点 5。然而，为了不让老鼠走到点 5 从而再走到点 0，它必须先走到点 5，而不能走到点 4。
   

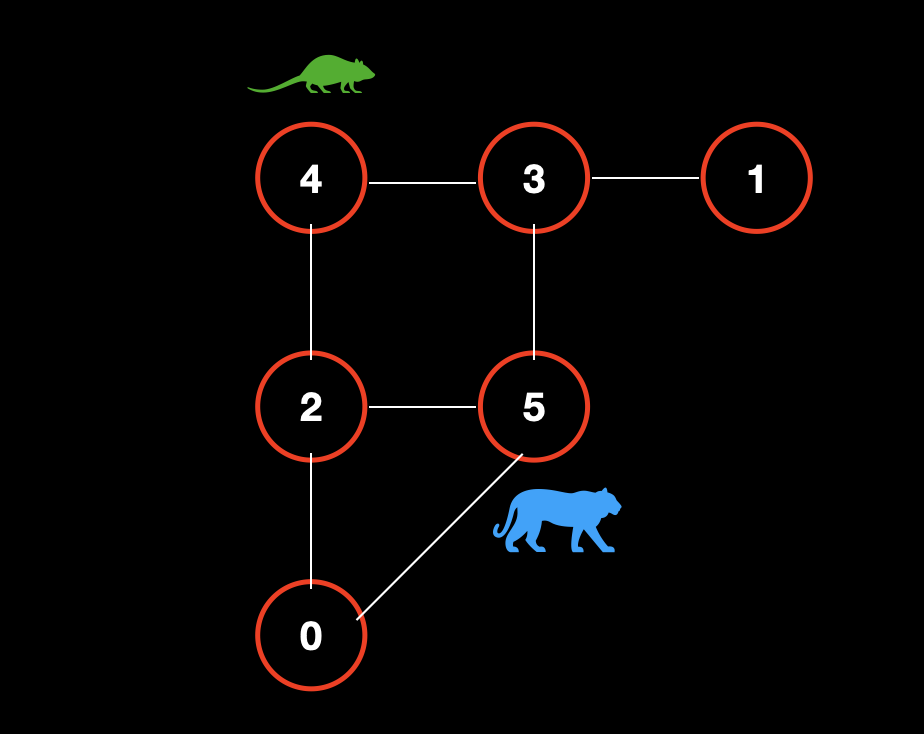
4. 老鼠走。此时，老鼠只剩下一种选择，既，走到点 4。
   

5. 猫咪走。此时，猫咪看似有点 2 和点 3 两种选择。然而，为了不让老鼠走到点 2 从而走到点 0，它必须回到点 2，而不能去点 3。
   

6. 老鼠走。此时，老鼠又只能走到点 3。也就是整体状态又回到了第二步。
   

如果游戏继续进行下去，就会重复步骤 2 到 6，因此，他们必定会得到平局的结果。

# 动态规划思路

状态定义：使用 f(k, i, j) 表示老鼠在 i ，猫咪在 j ，用 k 表示下一步该谁走。

无论对于老鼠还是猫咪来说，他们的下一步都可以走到自己此时所在点能连到的边。
也就是 f(k, i, j) ，可以有如下转移：

for x in g[i]:  # 下一状态老鼠走

    f(k + 1, x, j)  # 下一状态

for y in g[j]:  # 下一状态猫咪走

    f(k + 1, i, y)  # 下一状态

我们根据题意使用：1 表示老鼠赢，2 表示猫咪赢，0 表示平局。则对于老鼠和猫来说都是能选 1 就选 1，没法选 1 优先选 0（尽可能获胜，无法获胜尽量平局）。

老鼠和猫咪可走的点都是 1~n ，所以他们的可走步数最多只有 $2{n^2}$ 种。对应状态上，就是老鼠和猫咪都走 ${n^2}$ （注意这里不是 n ，因为题目没说不能走重复格子），所以总共是 $2{n^2}$ 。

所以总步数 ( k ) 大于 $2{n^2}$ 的时候，必然出现重复状态，也就是会平局。

但是，当 k 的取值范围取到 $2{n^2}$ 的极限值的时候，总时间复杂度还要乘以两个 n （老鼠和猫咪的取值，对应状态定义中 i 和 j 的范围），最终，时间复杂度达到 $2{n^4}$ ，最后超时。

但是但是但是，再想一下，其实老鼠和猫咪的点并没有都是 1~n ，因为它们是不能往回走的，也就是说无论是老鼠还是猫只要走一步就要减少一格，因此他们每人最多走 n 格（因为不能往回了），所以，他俩一人一步，只能走 $2{n}$ 步。

# Code

def catMouseGame(self, graph: List[List[int]]) -> int:

    n = len(graph)

    f = [[[-1] * (n + 2) for _ in range(n + 2)] for _ in range(n * 2 + 2)]

    def dfs(k, i, j):

        # print('k, i, j', k, i, j)

        v = f[k][i][j]

        # 记忆化搜索，只搜索有效状态 

        # 用 -1 表示已经搜索过了 可以直接返回

        if v != -1:

            return v

        if k > 2 * n: # 平局

            f[k][i][j] = 0

            return 0

        if i == 0:  # 老鼠进洞 老鼠赢

            f[k][i][j] = 1

            return 1

        if i == j:  # 老鼠和猫在一个点 猫咪赢

            f[k][i][j] = 2

            return 2

        if k % 2 == 0:  # 老鼠走

            draws = 0 # 有无平局

            for x in graph[i]:

                t = dfs(k + 1, x, j) # 老鼠下一步结果

                if t == 1: # 老鼠走到 1 就赢

                    f[k][i][j] = 1

                    return 1

                if t == 0: # 老鼠走到 0 可以有平局

                    draws += 1

            if draws: # 平局返回 0

                f[k][i][j] = 0

                return 0

            f[k][i][j] = 2

            return 2 # 老鼠没赢 也没能平局 猫赢

        else:

            draws = 0

            for y in graph[j]:

                if y == 0:  # y 是洞口 猫不能走

                    continue

                t = dfs(k + 1, i, y)

                if t == 2:  # 猫赢

                    f[k][i][j] = 2

                    return 2

                if t == 0:

                    draws += 1

            if draws: # 平局返回 0

                f[k][i][j] = 0

                return 0

            f[k][i][j] = 1

            return 1

    # 初始状态老鼠先走，老鼠在 1 猫咪在 2

    return dfs(0, 1, 2)