首页 算法 图论

# 前置文章

Spfa 简单应用

Bellman-Ford 简单应用

# 图论之求负环问题模型

给出一张有向图或者无向图，其中每条边都有权值（距离），权值有正有负，如果图中存在一个环，这个环的所有边权值之和是负数，则称之为 “负环”。

# 负环对算法的影响

根据我们的更新条件，当存在一条边 {a, b, w} 满足 dist[x] > dist[b] + w 则可以进行更新，但是如果有负环，那么该更新过程永远都不会结束。

  1. 正环图中的更新

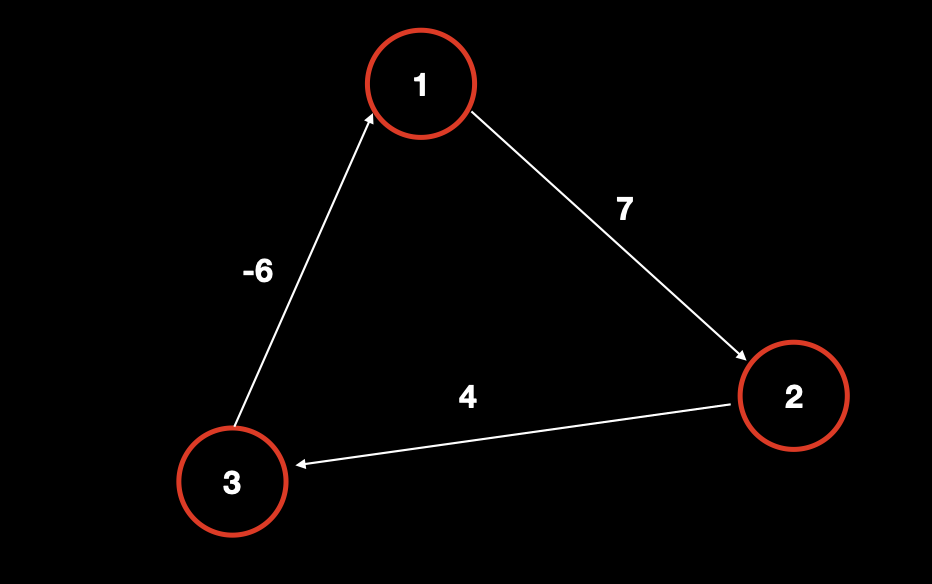
    在一个正环图中，我们以 点 1 为源点，求 点 1 到 点 2 的最短距离，看一下他们的更新情况。从 点1 到 点2 有两种走法：

    1. 直接从 点1 到 点2 。既，直接初始化该最短距离为 7 ，记作 dist[2]=7 。

    2. 从 点1 出发经过环再到达 点2 。既， 1 -> 2 -> 3 -> 1 -> 2 ，那么这条路径为 7 + 4 + (-6) + 7 == 12 ，而以前的最短距离是 7 ，那么此时无法再更新路径 dist[2] 。

      并且，因为整个环上的权值之和是正数，所以再循环下去这个路径值只会越来越大，更加无法更新 dist[2] 。

  2. 负环图中的更新

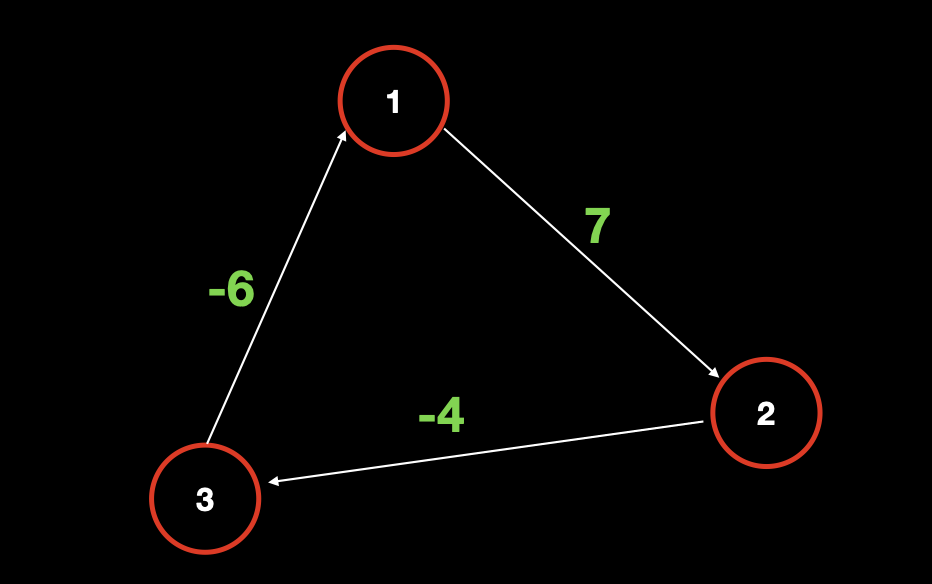
    在负环图中，仍然以 点 1 为源点，求 点 1 到 点 2 的最短距离，依然是两种情况：

    1. 直接从 点1 到 点2 ，既初始化该最短距离为 7 ，记作 dist[2]=7 。

    2. 从 点1 出发经过环再到达 点2 。既， 1 -> 2 -> 3 -> 1 -> 2 ，那么这条路径为 7 + (-4) + (-6) + 7 == 4 ，而以前的最短距离 dist[2]=7 ，我们发现从 点1 出发在环上绕一圈，再到达 点2 ，反而使最短距离变小了，更新后的最短距离是 dist[2]=4 ，这个距离是由环上所有边的权重之和 加上 上一个该点的最短距离组成。

      并且，因为整个环的权重之和是负数，所以每经过一次环， dist[2] 都会被更新，这就造成了我们算法陷入死循环。

# 判断是否有负环

  1. 在 Spfa 算法中，每次更新最短距离后，都会把被更新的点入队，因此，我们只需要统计每个点入队的次数。

    如果一个点入队了 n 次，也就代表它更新了 n 次，说明它经过了 n 条边，两个点连成一条边，所以它至少经过了 n+1 个点，但是我们只有 n 个点，根据抽屉原理，必然有一个点被经过了两次，也就说明图中存在环，使得路径回到了经过两次的那个点。

    并且，我们知道路径想要更新，那必须是当前计算出的最短距离小于目前该点的最短距离（比如： dist[2]=7 和 绕环一周后的 4 ）。

    假设当前 dist[2]=7 ，那么计算出 4 这个结果是通过环权重总和 + dist [2] 得到，已知 dist[2] 是确定的，想要让这个计算结果 (4) 比 dist[2] 更小，则环的权重总和就必须是负数。

    这样我们就得到了一个负环。

  2. 还有另外一种方式，依旧是使用 Spfa 算法，统计从起点到任意一个 点i 的最短路经过的边数，若 点i 对应边数 cnt[i] >= n , 则也说明存在负环。

    正确性理解与上面的方法 1 相同。方法 1 通过入队次数来推断路径经过的边数量，而本方法直接统计起点到点 i 的经过的边数量。所以该方法更方便，更容易理解一点。

# AcWing 904. 虫洞

农夫约翰在巡视他的众多农场时，发现了很多令人惊叹的虫洞。

虫洞非常奇特，它可以看作是一条 单向 路径，通过它可以使你回到过去的某个时刻（相对于你进入虫洞之前）。

农夫约翰的每个农场中包含 N 片田地，M 条路径（双向）以及 W 个虫洞。

现在农夫约翰希望能够从农场中的某片田地出发，经过一些路径和虫洞回到过去，并在他的出发时刻之前赶到他的出发地。

他希望能够看到出发之前的自己。

请你判断一下约翰能否做到这一点。

下面我们将给你提供约翰拥有的农场数量 F，以及每个农场的完整信息。

已知走过任何一条路径所花费的时间都不超过 10000 秒，任何虫洞将他带回的时间都不会超过 10000 秒。

输入格式
第一行包含整数 F，表示约翰共有 F 个农场。

对于每个农场，第一行包含三个整数 N,M,W。

接下来 M 行，每行包含三个整数 S,E,T，表示田地 S 和 E 之间存在一条路径，经过这条路径所花的时间为 T。

再接下来 W 行，每行包含三个整数 S,E,T，表示存在一条从田地 S 走到田地 E 的虫洞，走过这条虫洞，可以回到 T 秒之前。

输出格式
输出共 F 行，每行输出一个结果。

如果约翰能够在出发时刻之前回到出发地，则输出 YES，否则输出 NO。

数据范围

1≤F≤5
1≤N≤500,
1≤M≤2500,
1≤W≤200,
1≤T≤10000,
1≤S,E≤N

输入样例

2
3 3 1
1 2 2
1 3 4
2 3 1
3 1 3
3 2 1
1 2 3
2 3 4
3 1 8

输出样例

NO
YES

# 题目描述

说是农夫的农场里存在一种 “虫洞”，虫洞可以看做一种单向的道路，可以回到过去的某一时刻。问题是 农夫可以从任意的点 i 出发，是否可以通过虫洞，再回到点 i，看到出发前的自己。

# 题目分析

本题是一个比较简单的负环模板型问题。我们把农夫的每一个农场看做 点，把连接农场田地的路径看做 边，把经过每条路径所需要的时间看做 边的权重，并且已知虫洞的作用是回到 T 秒之前，所以我们把虫洞看做是单向负权边，这样，本题实际上就是求从任意一个点出发，是否存在一个负环（回到起点）。所以根据前面的小节的分析直接使用 Spfa 求一下是否存在负环就可以了。

# Code

在实现上，本题还有一个地方需要注意，既，我们不知道以哪个点作为起点。

为了解决这个问题，可以使用虚拟源点的思想，既，使用一个虚拟源点，向所有的点连接一条权重为 0 的边。这样，原图中有负环就等价于新图中有负环，而新图我们可以直接从虚拟源点出发寻找负环，因为虚拟源点可以遍历到所有其他点，并且到所有其他点的权重是 0，不影响最终答案。

实现上，我们把所有点都入队，并且标记为距离为 0，相当于设置一个不存在的虚拟源点连接到其他点一条权重为 0 的边。

#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, M = 5210;
int n, m1, m2;
int dist[N], cnt[N], q[N];
bool st[N];
int h[N], e[M], ne[M], w[M], idx;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa() {
    memset(dist, 0x3f, sizeof dist);
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);
    
    int hh = 0, tt = 0;
    // 所有点都入队
    for (int i = 1; i <= n; i ++ ) {
        q[tt ++ ] = i;
        st[i] = true;
    }
    while (hh != tt) {
        int t = q[hh ++ ];
        if (hh == N) hh = 0;
        st[t] = false;
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                // 统计边的条数 由 t -> j 则 j 的最短路径增加一条边
                cnt[j] = cnt[t] + 1; 
                if (cnt[j] >= n) return true;
                if (!st[j]) {
                    q[tt ++ ] = j;
                    if (tt == N) tt = 0;
                    st[j] = true;
                }
            }
        }
    }
    return false;
    
}
int main() {
    int T;
    cin >> T;
    while (T -- ) {
        memset(h, -1, sizeof h);
        idx = 0;
        cin >> n >> m1 >> m2;
        while (m1 -- ) {
            int a, b, c;
            cin >> a >> b >> c;
            add(a, b, c), add(b, a, c); // 田地的道路是双向边
        }
        while (m2 -- ) {
            int a, b, c;
            cin >> a >> b >> c;
            add(a, b, -c); // 虫洞是单向的负权边
        }
        bool res = spfa();
        if (res) puts("YES");
        else puts("NO");
    }
    return 0;
}
# AcWing 361. 观光奶牛
给定一张 L 个点、P 条边的有向图，每个点都有一个权值 f [i]，每条边都有一个权值 t [i]。
求图中的一个环，使 “环上各点的权值之和” 除以 “环上各边的权值之和” 最大。
输出这个最大值。
注意：数据保证至少存在一个环。
输入格式
第一行包含两个整数 L 和 P。
接下来 L 行每行一个整数，表示 f [i]。
再接下来 P 行，每行三个整数 a，b，t [i]，表示点 a 和 b 之间存在一条边，边的权值为 t [i]。
输出格式
输出一个数表示结果，保留两位小数。
数据范围
2≤L≤1000,
2≤P≤5000,
1≤f[i],t[i]≤1000

输入样例
5 7
30
10
10
5
10
1 2 3
2 3 2
3 4 5
3 5 2
4 5 5
5 1 3
5 2 2

输出样例
6.00

# 题目描述
给定一个 L 个点，P 条边的有向图，每个点的权值为 f[i] ，每条边的权值为 t[i] ，求图中是否存在一个环，使得 环上∑f[i]∑t[i]\frac{\sum f[i]}{\sum t[i]}（后面称为 公式 ） 的值最大。
# 题目分析
图论问题中，形如此类问题：max (∑x∑y\frac{\sum x}{\sum y})，被称为 01 规划问题。对于这类问题，通常使用二分法来解决。
根据数据范围 1≤f[i],t[i]≤1000 可以知道，想让 公式 最大，最大的值时，就是让所有的 f [i] 为 1000 ，所有的 t[i] 为 1 ，结果为 1000 ，所以我们可以知道公式最终的结果范围是 (0, 1000] 。
假如，对上述的公式范围进行二分，得到答案 mid，那么，我们就可以根据：给定图中是否有一个环，可以使得 公式 > mid，来调整 mid 的范围。如果存在这样的环，那么我们就可以增加 mid 的值，反之，减小 mid 的值。
如此，问题就变成了，如何判断图中是否存在一个环，使得 公式 > mid。
首先，把公式做一下变形：∑fi∑ti>mid\frac{\sum f_i}{\sum t_i}>mid，因为其中的权重全部是正数，所以可以变成∑fi>∑ti∗mid{\sum f_i}>{\sum t_i}*mid，再变换一下，把他们移动到一边，得到：∑fi−∑ti∗mid>0{\sum f_i}-{\sum t_i}*mid>0，因为是累加是加法操作，所以我们把累加符号提出来，公式变成：∑(fi−ti∗mid)>0\sum (f_i-t_i*mid)>0。
根据上面的推导，我们要判断图中是否存在一个环，使得公式∑(fi−ti∗mid)>0\sum (f_i-t_i*mid)>0 成立。
spfa 算法有一个性质，当图中存在 点权 和 边权 两种权重的时候，可以把他们放到一起来看，既，把 点权 存放到 边权 中。
在本题我们就可以用这个性质，把边的权重从tit_i 替换成fi−ti∗midf_i-t_i*mid。这样，本题就变成了图中是否存在一个正环。
那么，求正环和负环是一个对称的问题，我们可以直接 spfa 求最长路的同时判断是否存在正环就可以了。
# Code
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010, M = 5010;
int h[N], wf[N], e[M], ne[M], idx;
int q[N], cnt[N];
int wt[M];
double dist[N];
bool st[N];
int n, m;
void add(int a, int b, int  c) {
    e[idx] = b, wt[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa(double mid) {
    memset(dist, 0, sizeof dist);
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    int hh = 0, tt = 0;
    for (int i = 1; i <= n; i ++ ) {
        q[tt ++ ] = i;
        st[i] = true;
    }
    while (hh != tt) {
        int t = q[hh ++ ];
        if (hh == N) hh = 0;
        st[t] = false;
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            // 求最长路径 此处是小于号  
            //t -> j 权重是点 t 的权重和边的权重乘 mid
            if (dist[j] < dist[t] + wf[t] - wt[i] * mid) {
                dist[j] = dist[t] + wf[t] - wt[i] * mid;
                cnt[j] = cnt[t] + 1;
                if (cnt[j] >= n) return true;
                if (!st[j]) {
                    q[tt ++ ] = j;
                    if (tt == N) tt = 0;
                    st[j] = true;
                }
            }
        }
    }
    return false;
}
int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i ++ ) cin >> wf[i];
    while (m -- ) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    double l = 0, r = 1e6;
    //double 类型的精度问题 大于一个比较小的数 既为 0
    while (r - l > 1e-4) {
        double mid = (l + r) / 2;
        if (spfa(mid)) l = mid;
        else r = mid;
    }
    printf("%.2lf\n", r);
    return 0;
}
# AcWing 1165. 单词环
我们有 n 个字符串，每个字符串都是由 a∼z 的小写英文字母组成的。
如果字符串 A 的结尾两个字符刚好与字符串 B 的开头两个字符相匹配，那么我们称 A 与 B 能够相连（注意：A 能与 B 相连不代表 B 能与 A 相连）。
我们希望从给定的字符串中找出一些，使得它们首尾相连形成一个环串（一个串首尾相连也算），我们想要使这个环串的平均长度最大。
如下例：
ababc
bckjaca
caahoynaab
第一个串能与第二个串相连，第二个串能与第三个串相连，第三个串能与第一个串相连，我们按照此顺序相连，便形成了一个环串，长度为 5+7+10=22（重复部分算两次），总共使用了 3 个串，所以平均长度是 223≈7.33。
输入格式
本题有多组数据。
每组数据的第一行，一个整数 n，表示字符串数量；
接下来 n 行，每行一个长度小于等于 1000 的字符串。
读入以 n=0 结束。
输出格式
若不存在环串，输出”No solution”，否则输出最长的环串的平均长度。
只要答案与标准答案的差不超过 0.01，就视为答案正确。
数据范围
1≤n≤10^5

输入样例
3
intercommunicational
alkylbenzenesulfonate
tetraiodophenolphthalein
0

输出样例
21.66

# 题目描述
给出 n 个字符串，当一个字符串的最后两个字符和另一个字符串的前两个字符相同的时候，这两个字符串可以拼接起来。如此拼接，则有可能拼出一个环，用环中边的总权重除以环的数量，就得到了环的平均长度，本题的目标是求环的最大平均长度。
# 题目分析
本题在建图上，有一个小小的陷阱，很容易想到的建图方法是：把每个字符串当做一个点，如果能连接到另一个字符串，则连接一条边。但是我们注意一下数据范围 1≤n≤10^5 ，字符串一共有10510^5 个，那如果两两连接一条边，边的数量将达到101010^{10} ，无论是空间还是时间都是会爆掉的，所以要换一种建图的方法。
我们把每个字符串当做一条边，把字符串的头部和尾部的两个字母看做点，把字符串的长度看做是边的权重。按照这种建图方式，我们看一下题面给出的示例中的图：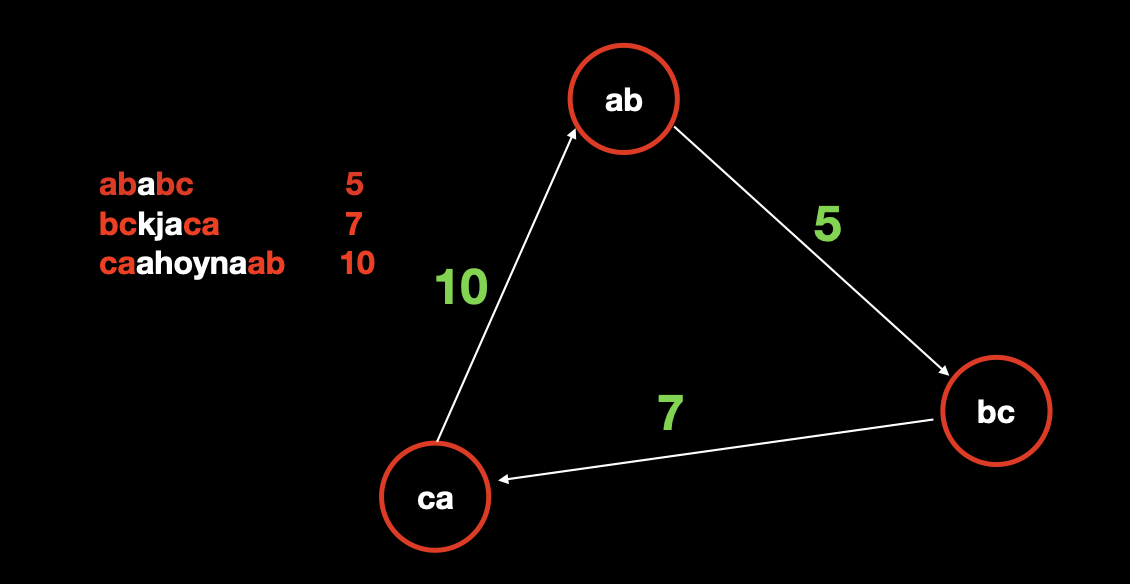
按照这种方式建图，点由两个小写字母组成，每个小写字母共有 26 个，因此点的数量就是 26*26==676 个点，而边的数量就是字符串的数量，既，10510^5。
当建图之后，我们要求的目标是图中是否存在一个环使得，环中边权之和除以边权数量的结果最大。，也就是求max(∑wi∑1)max(\frac{\sum w_i}{\sum 1})，其中分母为环中所有边权之和，分母为环中所有边权数量。如此，我们就将这道题完完全全的转换成和上题一样的题目。
那我们再按照上题的思路分析一下：
  1. 二分法的范围是 (0，1000] ，其中 1000 为10510^5 个边均取最大值；
  2. 公式转换：∑wi∑1>mid\frac{\sum w_i}{\sum 1}>mid，因为分子和分母都是正数，所以可以把分子移动到右面，得到:∑wi>mid∗∑1\sum w_i>mid*\sum1，把他们都移动到一侧，得到：∑wi−∑1∗mid>0\sum w_i-\sum1 * mid>0 ，最后把求和符号提出来，得到：∑wi−1∗mid>0\sum w_i-1*mid>0。
  3. 所以，我们把边的权重看做是wi−midw_i-mid。
  4. 对于每个 mid 以上面的最终公式作为权重，判断是否有正环。
# Code
注意本题实现上还有一个小细节，题目给出了条件 "可能不存在环串"，如何判断不存在环这种情况呢？
注意我们是把公式wi−midw_i-mid 作为边权的，而使得这个公式最大的 mid 值是 0，因为我们要判断的是正环，根据更新规则（权重大的更新权重小的），权重越大越可能出现正环，所以我们只要判断 mid 等于 0 时候，是否存在正环就可以判断出是否有解。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 700, M = 100010;
int h[N], w[M], e[M], ne[M], idx;
int q[N], cnt[N];
double dist[N];
bool st[N];
int n;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa(double mid) {
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    
    int hh = 0, tt = 0;
    for (int i = 0; i < 676; i ++ ) {
        q[tt ++ ] = i;
        st[i] = true;
    }
    int count = 0; // 统计 spfa 的迭代总次数
    while (hh != tt) {
        int t = q[hh ++ ];
        if (hh == N) hh = 0;
        st[t] = false;
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist[j] < dist[t] + w[i] - mid) {
                dist[j] = dist[t] + w[i] - mid;
                cnt[j] = cnt[t] + 1;
                // 此处是经验之举 当 spfa 迭代一定次数是，我们就认为出现环
                // 不加会超时
                if (++ count > 2 * n) return true;
                if (cnt[j] >= N) return true;
                if (!st[j]) {
                    q[tt ++ ] = j;
                    if (tt == N) tt = 0;
                    st[j] = true;
                }
            }
        }
    }
    return false;
}
int main() {
    while (scanf("%d", &n), n) {
        char str[1010];
        memset(h, -1, sizeof h);
        idx = 0;
        for (int i = 0; i < n; i ++ ) {
            scanf("%s", str);
            int len = strlen(str); // 字符串长度
            if (len >= 2) {
                // 任意使用一种方式来表示字符串的头部尾部两个数 这里使用数字。
                int left = (str[0] - 'a') * 26 + str[1] - 'a';
                int right = (str[len - 2] - 'a') * 26 + str[len - 1] - 'a';
                add(left, right, len); // 读入边
            }
        }
        if (!spfa(0)) puts("No solution");
        else {
            double l = 0, r = 1000;
            while (r - l > 1e-4) {
                double mid = (l + r) / 2;
                if (spfa(mid)) l = mid;
                else r = mid;
            }
            printf("%lf\n", r);
        }
    }
    return 0;
}
END
   
 更新于   阅读次数  次
请我喝[茶]~(￣▽￣)~*
A Cat Without Sugar 微信支付
微信支付
A Cat Without Sugar 支付宝
支付宝