首页 算法 图论

# 前置知识

差分约束问题的常规思路

# 拓扑排序

对于一个图，图中所有的点可以构成一个序列，对于图中的每条边 x->y ，在序列中 x 都出现在 y 的前面，则称这个序列是这个图的拓扑序列，这个图是拓扑图。

也就是说，当用拓扑排序排好之后，整个图中的边都是从前往后的。

例如下图中，可以组成一个序列 [1,2,3] ，其中三条边 1->2 ， 2->3 ， 1->3 。均是由前面的点指向后面的点。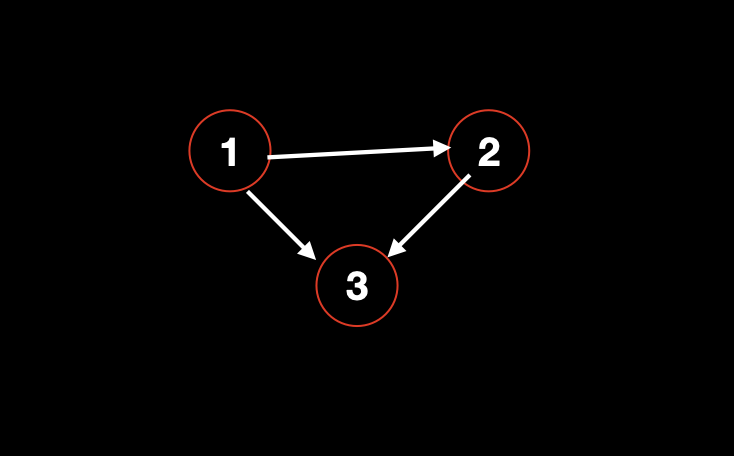

如果把边 1->3 变成 3->1 ，那么图中就会出现环，而边 3->1 则不满足拓扑序列的条件，说明拓扑图一定是五环的，所以拓扑图又是有向无环图。

# 求拓扑序列的思路

有向图中点的入度：有多少条边指向该点；

有向图中点的出度：有多少条边从该点出去；

例如：上图中的三个点中：

  1. 对于点 1 来说，没有边指向它，所以它的入度是 0，而有两条边从它出去，所以它的出度是 2；

  2. 对于点 2 来说，有一条边指向它，所以它的入度是 1，有一条边从它出去，所以它的出度也是 1；

  3. 对于点 3 来说，有两条边指向它，所以它的入度是 2，没有边从它出去，所以它的出度是 0；

首先，考虑拓扑序列的起始点，在例子中，我们发现 点1 是入度为 0 的点，这意味着，没有任何一条边在它前面，因此它可以作为一个起始点，也就是说可以把入度为 0 的点作为起始点。

然后，我们结合拓扑图的定义，使用 BFS 来完成拓扑排序。

# 模板 Code

q[N]; // 添加所有入度为 0 的点进入队列
while (q.size()) {
    int t = q.pop_first(); // 取出队头元素
    // 枚举所有 t 指向的边 j。
    for (int i = h[t]; ~i; i = ne[i]) {
        din[j] -- ; // 模拟删除掉 t->j 这条边，让 j 的入度减一；
        // 假如点 j 入度为 0，说明它前面没有点了，既这之后出现的点不可能指向它。
        // 那么我们就可以把它入队。
        if (!din[j]) {
            q[++ tt] = j;
        }
    }
}

# AcWing 1191. 家谱树

有个人的家族很大，辈分关系很混乱，请你帮整理一下这种关系。

给出每个人的孩子的信息。

输出一个序列，使得每个人的孩子都比那个人后列出。

输入格式
第 1 行一个整数 n，表示家族的人数；

接下来 n 行，第 i 行描述第 i 个人的孩子；

每行最后是 0 表示描述完毕。

每个人的编号从 1 到 n。

输出格式
输出一个序列，使得每个人的孩子都比那个人后列出；

数据保证一定有解，如果有多解输出任意一解。

数据范围

1≤n≤100

输入样例

5
0
4 5 1 0
1 0
5 3 0
3 0

输出样例

2 4 5 3 1

# 题目描述

整理一个家族的族谱。（给出一个有向无环图，输出拓扑序列。）

# 题目分析

拓扑排序的模板题。

我们把每一个人都看做图的一个节点，如果 a 有一个儿子是 b，那么我们就连接一条有向边 a->b ，用这种建图方式，我们就创建出来一个有向无环图，题目要求我们每个人的孩子都比那个人后输出，也就是输出的序列里面，所有的边都是从 前 指向 后，也就是拓扑排序。

# Code

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, M = N * N;
int n, m;
int h[N], e[M], ne[M], idx;
int q[N], din[N];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// 拓扑排序模板
void topsort() {
    int hh = 0, tt = -1;
    // 把所有度数为 0 的起点入队
    for (int i = 1; i <= n; i ++ ) {
        if (!din[i])
            q[++ tt] = i;
    }
    while (hh <= tt) {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (-- din[j] == 0) {
                q[ ++ tt] = j;
            }
        }
    }
}
int main() {
    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i ++ ) {
        int son;
        while (cin >> son, son) {
            add(i, son);
            din[son] ++;
        }
    }
    topsort();
    for (int i = 0; i < n; i ++ ) cout << q[i] << ' ';
    cout << endl;
    return 0;
}
# AcWing 1192. 奖金
由于无敌的凡凡在 2005 年世界英俊帅气男总决选中胜出，Yali Company 总经理 Mr.Z 心情好，决定给每位员工发奖金。
公司决定以每个人本年在公司的贡献为标准来计算他们得到奖金的多少。
于是 Mr.Z 下令召开 m 方会谈。
每位参加会谈的代表提出了自己的意见：“我认为员工 a 的奖金应该比 b 高！”
Mr.Z 决定要找出一种奖金方案，满足各位代表的意见，且同时使得总奖金数最少。
每位员工奖金最少为 100 元，且必须是整数。
输入格式
第一行包含整数 n,m，分别表示公司内员工数以及参会代表数。
接下来 m 行，每行 2 个整数 a,b，表示某个代表认为第 a 号员工奖金应该比第 b 号员工高。
输出格式
若无法找到合理方案，则输出 “Poor Xed”；
否则输出一个数表示最少总奖金。
数据范围
1≤n≤10000,
1≤m≤20000

输入样例
2 1
1 2

输出样例
201

# 题目描述
公司发奖金的故事。给出一些不等式条件，求公司需要给出的最少的总奖金。
# 题目分析
把员工看做点，代表提出的意见看做不等式，使用差分约束的思路建图。
看到本题核心的不等式条件，我们发现这似乎是一道差分约束的题目。
但是我们分析题目，发现本题求的是最少的总奖金，这也意味着，当我们得到一个不等式的时候，只能增加一块钱，也就是说明按照差分约束的思路，将不等式转换为图之后，图中所有边的权重恒定为 1，说明图中一定不存在环，因为存在环说明边权重一定小于等于 0。
不等式转换后的图，不存在环，又是有向图，所以这就是一个有向无环图，又称拓扑图。
所以，本题我们只需要求一下拓扑排序，然后求一遍最长路就能得到最少的总奖金啦。（参考文章：差分约束，求 “最少” 需要用最长路。）
# Code
#include <iostream>
#include <cstring>
using namespace std;
const int N = 10010, M = 20010;
int n, m;
int h[N], e[M], ne[M], idx;
int q[N], din[N];
int dist[N];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool topsort() {
    int hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++ ) {
        if (!din[i]) q[ ++ tt] = i;
    }
    while (hh <= tt) {
        int t = q[ hh ++ ];
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (-- din[j] == 0) q[ ++ tt] = j;
        }
    }
    return tt == n - 1; // 判断有没有环 有环则无解。
}
int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while (m -- ) {
        int a, b;
        cin >> a >> b;
        add(b, a); // 不等式转换成图的 连边规则。
        din[a] ++ ;
    }
    if (!topsort()) puts("Poor Xed");
    else {
        // 初始化每个人最少 100 块钱
        for (int i = 1; i <= n; i ++ ) dist[i] = 100;
        // 拓扑排序求最大值 依次按照顺序求就行
        for (int i = 0; i < n; i ++ ) {
            int j = q[i];
            // 求长路 
            for (int k = h[j]; ~k; k = ne[k])
                dist[e[k]] = max(dist[e[k]], dist[j] + 1);
        }
        int res = 0;
        for (int i = 1; i <= n; i ++ ) res += dist[i];
        cout << res << endl;
    }
    return 0;
}
# AcWing 164. 可达性统计
给定一张 N 个点 M 条边的有向无环图，分别统计从每个点出发能够到达的点的数量。
输入格式
第一行两个整数 N,M，接下来 M 行每行两个整数 x,y，表示从 x 到 y 的一条有向边。
输出格式
输出共 N 行，表示每个点能够到达的点的数量。
数据范围
1≤N,M≤30000
输入样例
10 10
3 8
2 3
2 5
5 9
5 9
2 3
3 9
4 8
2 10
4 9

输出样例
1
6
3
3
2
1
1
1
1
1

# 题目描述
给出一个拓扑图，求分别统计每个点出发 能够到达的点的数量。

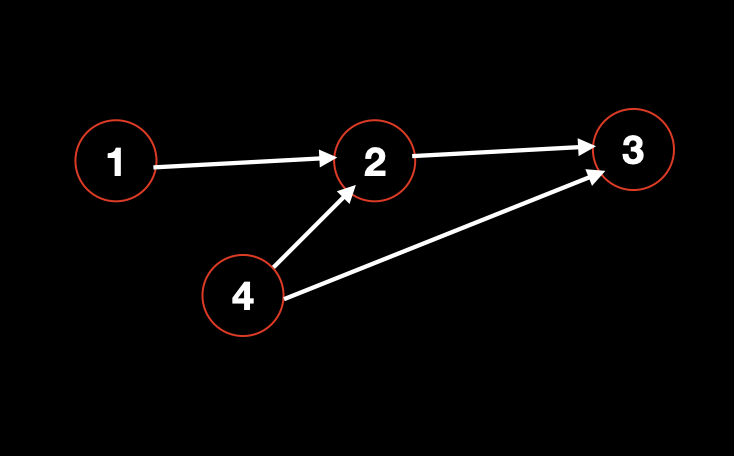
如上图所示:
  1. 从点 1 出发，可以到达点 1,2 和 3，所以数量就是 3；
  2. 从点 2 出发，可以到达点 2 和 3，所以数量就是 2；
  3. 从点 3 出发，只能到达它自己，所以数量就是 1；
  4. 从点 4 出发，可以到达点 4,2 和 3，所以数量就是 3；
因此最终结果是：3,2,1,3。
# 题目分析
通过题面，我们发现从每个点出发，能到达的点的数量，就是 该点本身 加上 它后面所有点能到达的点的数量。
因此，我们就能使用动态规划的思路来解决该问题。
假设有两条边 i->j1 和 i->j2 ，我们让 f [i] 表示点 i 能到达的点的数量，那么根据上述的思路，就可以得到：
f[i] = 1 + f[j1] + f[j2]

那么此时又出现了一个新的问题，在上面的公式中，我们求当前的 f [i] 的时候，使用了 i 后面的点的 f 数组值，我们如何保证，当计算 f [i] 时候，它后面点的 f 数组值已经被计算出来了呢？
观察题面，本题是有向无环图，也即是拓扑图，而拓扑图有一个重要的特性：拓扑排序后，对于任意的一条边 {x->y} x 都会出现在 y 的前面。
也就是说，只要我们对整个图拓扑排序一遍，然后把排序结果倒序，就可以保证 y 一定出现在 x 前面，那么当计算点 x 的 f 值时候，它所有可达点 y 的 f 值 都已经被计算出来了。
# Code
在实现的时候，有一个需要注意的地方，我们在实现的的时候，要把拓扑序列遍历一遍，对于其中的每个点 都要遍历这个点的所有边，这个操作会让时间复杂度达到O(n2)O(n^2)，其中 n 的数据范围是3∗1043*10^4，这个操作的时间复杂度就是9∗1089*10^8，会超时。因此我们要优化一下。
参考以前学过的状态压缩的思路，我们可以把 f [i] 看做一个二进制数，二进制的第 j 位如果是 1，表示当前 i 可以到 j，如果是 0，则表示当前 i 不能到点 j。
使用这种方式，可以把 N 位的二进制数压缩成N/32N/32 + 1 个无符号的 32 位 unsigned int 进行存储。如此，将时间复杂度压缩到N(N+M)/32N(N+M)/32，空间使用则约为N2/8N^2/8（一个字节的八个比特位均能存储一个 1/0）。
这个操作我们可以用 C++ STL 中的 bieset 来完成。
#include <iostream>
#include <cstring>
#include <bitset>
using namespace std;
const int N = 30010, M = 30010;
int n, m;
int h[N], e[M], ne[M], idx;
int q[N], din[N];
bitset<N> f[N];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// 拓扑排序模板
void topsort() {
    int hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++ )
        if (!din[i]) q[ ++ tt] = i;
    while (hh <= tt) {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (-- din[j] == 0) {
                q[ ++ tt] = j;
            }
        }
    }
}
int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while (m -- ) {
        int a, b;
        cin >> a >> b;
        add(a, b);
        din[b] ++ ;
    }
    topsort();
    // 如果 x 能到达 y1,y2 那么想求 f [x] 必须先求出 f [y1] 和 f [y2]
    // 而拓扑排序后 x 一定在它能到的点 (y1,y2) 的前面 所以这里需要倒序
    for (int i = n - 1; i >= 0; i -- ) {
        int j = q[i];
        // 初始化当前节点的 f 值为 1 表示节点自己能到自己
        f[j][j] = 1; 
        // 所有点 j 能到达的点 e [k]
        for (int k = h[j]; ~k; k = ne[k])
            // 那么 f [j] 就是 点 j 自身 和 所有 f [e [k]] 的并集
            // 二进制操作中就是 或运算
            f[j] |= f[e[k]];
    }
    for (int i = 1; i <= n; i ++ ) {
        cout << f[i].count() << endl;
    }
    return 0;
}
# AcWing 456. 车站分级
一条单向的铁路线上，依次有编号为 1, 2, …, n 的 n 个火车站。
每个火车站都有一个级别，最低为 1 级。
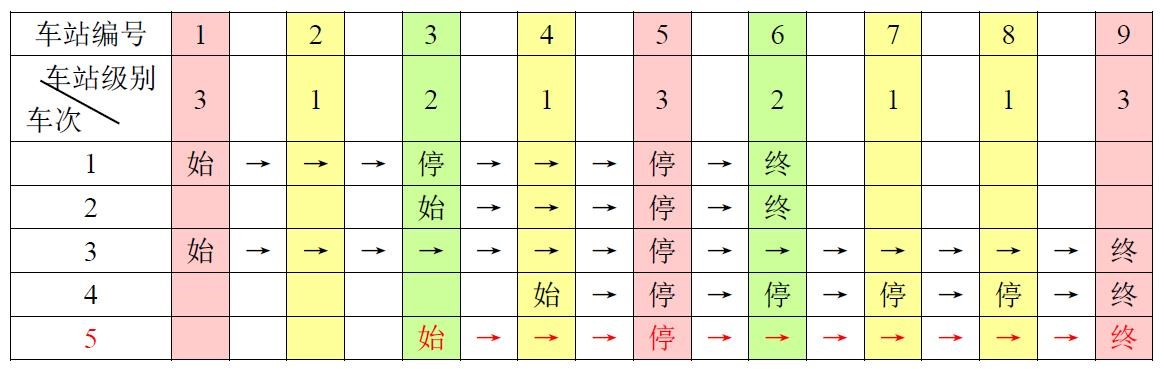
现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）
例如，下表是 5 趟车次的运行情况。
其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。
现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。
输入格式
第一行包含 2 个正整数 n,m，用一个空格隔开。
第 i+1 行（1≤i≤m）中，首先是一个正整数 si（2≤si≤n），表示第 i 趟车次有 si 个停靠站；接下来有 si 个正整数，表示所有停靠站的编号，从小到大排列。
每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
输出只有一行，包含一个正整数，即 n 个火车站最少划分的级别数。
数据范围
 1≤n,m≤1000

输入样例
9 3 
4 1 3 5 6 
3 3 5 6 
3 1 5 9 

输出样例
3

# 题目描述
神奇的铁路列车运行规则。
给出一条单向铁路线，线上有 n 个点作为车站，每个车站都有一个级别，每一趟列车的运行都要满足如下规则：如果他在第 x 站停靠了，那么所有级别 小于等于 第 x 站级别 的车站 也都需要停靠。已知起始站和终点站是必须停靠的，也就是说已知所有级别小于等于起始站和终点站的车站都必须停靠。
问题是给出 m 趟车次的运行情况，计算出 要满足 m 趟列车的运行，所有的火车站至少要分为几个不同级别。
# 题目分析
本题其实和本文的第二个题目 AcWing 1192. 奖金高度相似，不同点是在 1192 里面，明确的给出不等式条件，而本题的题面则是高度抽象，甚至都不太能分辨出是图论问题。
本题，如果从问题入手，就太抽象了（我刚读完题甚至都不明白问题啥意思）。我们可以先分析一下，读完题之后，比较清晰的线索：
  1. 停靠过的车站的等级 一定严格大于 没有停靠过的车站的等级；
  2. 每个车站都有一个级别，最低为 1 级；
综合线索 1 和 2，可以推理出本题最关键的结论：假如在 A 车站停靠了，而 B 车站没有停靠，则一定有一个不等式：A>=B+1，表示的含义是停靠的车站的级别 至少也要比 未停靠车站 的级别大 1。
回过头来，我们在看本题的最终问题：满足 m 趟列车，至少 要分为几个不同的级别。分析一下题目给出的示例：
  1. 示例中有 9 个火车站，共有 3 趟列车；
  2. 第一趟列车有四个停靠站，分别是 1,3,5,6；第二趟列车有三个停靠站，分别是 3,5,6；第三趟列车有三个停靠站，分别是 1,5,9；
我们可以以每个车站为点，第一辆车在 1 号车站停靠，而在 2 号车站未停靠，我们就可以列出一个不等式： 1号车站>=2号车站+1 ，然后根据差分约束的思路，把不等式转换成图，也就是 连接一条边由 2 号点指向 1 号点。使用这种方式，我们就建好了一个图。
由于求解的是 最少的级别，所以我们对这个图求最长路就可以了（参考差分约束）。
在一个拓扑图里面求最长路，与 1192 题完全的一致，因此不在赘述。
# Code
实现上，我们发现 n 和 m 的范围是 1000，也就是极限数据下，有 1000 个车站和 1000 趟列车。那么假设不等式数量（或者说连接边数量）也取最大，则是：有 500 个站停靠了，500 个是未停靠的（1000 分出来两个数相乘，能得到的最大值的组合）；
那么总的需要连接边的数量就是，1000 个列车，每个列车都会连接 500*500 个边，也就是 每个未停靠的车站 都向 所有停靠了的车站连接一条边，总量就是：1000∗500∗500=2.5∗1081000*500*500=2.5*10^8。
而这个数量可能会让时间和空间复杂度都超时。所以我们需要优化一下建图的策略。
我们可以建立一个虚拟源点，让左面的边到虚拟原点的权重是 0，右面的边到虚拟原点的权重是 1，就可以表示出左边每个点都到右边每个点都连了一条权重为 1 的边。
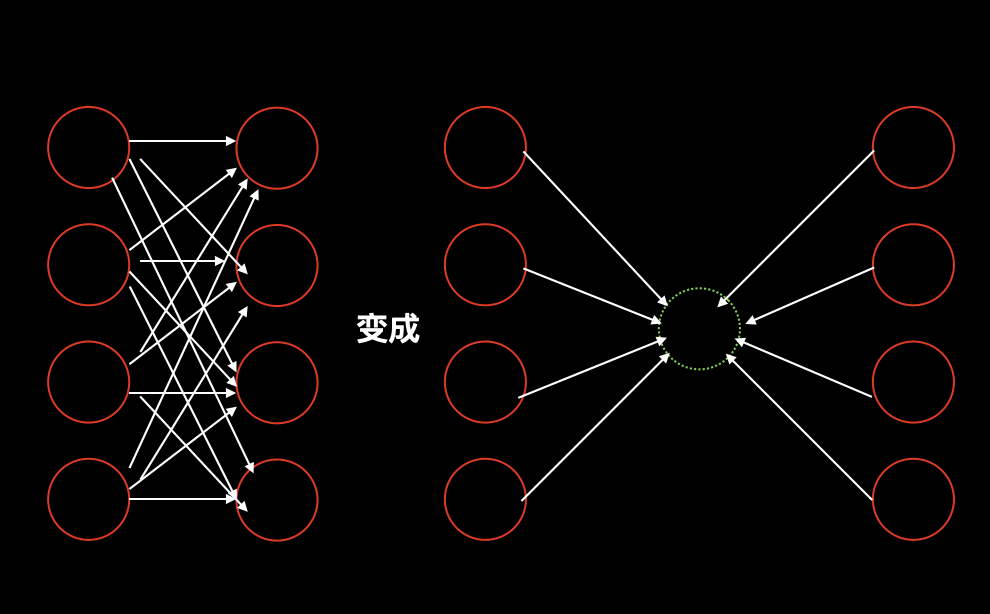
用这种方式就把复杂度由 n*m 降低到 n+m 。
#include <iostream>
#include <cstring>
using namespace std;
// 注意点的数量是 n+m 边极限数量 1000*1000
const int N = 2010, M = 1000010;
int h[N], e[M], w[M], ne[M], idx;
int q[N], din[N], dist[N]; // 求拓扑序和最大路径
bool st[N];
int n, m;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
    din[b] ++ ;
}
// 拓扑排序模板
void topsort() {
    int hh = 0, tt = -1;
    for (int i = 1; i <= n + m; i ++ ) {
        if (!din[i]) q[ ++ tt] = i;
    }
    while (hh <= tt) {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (-- din[j] == 0) q[ ++ tt] = j;
        }
    }
}
 
int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; i ++ ) {
        memset(st, 0, sizeof st);
        int cnt;
        scanf("%d", &cnt);
        // 初始站是最小值，终点站是最大值，
        // 为了方便后续计算，把初始站初始化成 n，终点站设置成 1
        int start = n, end = 1; 
        for (int j = 0; j < cnt; j ++ ) {
            int stop;
            scanf("%d", &stop); // 停靠的站
            start = min(start, stop);
            end = max(end, stop);
            st[stop] = true; // 判断是否是停靠的站
        }
        int ver = n + i; // 虚拟源点
        // 建边
        for (int j = start; j <= end; j ++ ) {
            // 如果是停靠的站 则是左面的边 指向虚拟源点 权重是 0
            // 否则是右面的边 虚拟原点指向它 权重是 1
            if (!st[j]) add(j, ver, 0);
            else add(ver, j, 1);
        }
    }
    topsort();
    // 初始化所有车站的距离
    for (int i = 1; i <= n; i ++ ) dist[i] = 1;
    // 求一下每个点的最大距离
    for (int i = 0; i < n + m; i ++ ) {
        int j = q[i];
        for (int k = h[j]; ~k; k = ne[k]) {
            dist[e[k]] = max(dist[e[k]], dist[j] + w[k]);
        }
    }
    // 在所有最长距离中求出最长的点 根据最终问题 只需要 求所有停靠的点就行了
    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, dist[i]);
    cout << res << endl;
    return 0;
}
END
  
 更新于   阅读次数  次
请我喝[茶]~(￣▽￣)~*
A Cat Without Sugar 微信支付
微信支付
A Cat Without Sugar 支付宝
支付宝