# 前置知识

lowbit(x) ：元素 x 在二进制表示下，其最低位的 1 和 后面的所有 0 构成的数。

比如：当 x=12 的时候，x 的二进制表示为 1100 ，那么它最低位的 1 和后面所有 0 构成的数二进制表示为 [100]、十进制是 4，所以 lowbit(12)=4 。

int lowbit(int x) {

    return x & -x;

}

# 树状数组

树状数组主要应用场景是给出一个长度为 n 的数组，对数组做如下两种操作：

1. 输出区间 [l,r] 所有数的和。
2. 将给出数组的第 i 个数加上 j。

要对完成这两个操作，我们如果使用数组，则操作 1 的时间复杂度是 O (n)，操作 2 的时间复杂度是 O (1)。

另外，我们还可以使用前缀和，则操作 1 的时间复杂度是 O (1)，而操作 2 的时间复杂度会变成 O (n)。

正所谓 “鱼与熊掌不可兼得”，那有没有什么办法讲两个操作的时间复杂度平衡一下呢？

这就轮到本文的主角树状数组出场了。使用树状数组可以把这两个操作的时间复杂度平衡到 O (logn)。

# 思路

树状数组的主要思想是使用 树的结构 维护 前缀和，又被称为二进制索引树（Binary Indexed Trees），通过二进制划分区间。

我们使用以下规则构建树状数组：

1. 树状数组中每个节点 t [x] 存储 以 x 为根的子树中 叶子结点值的 和（注意这里有两个关键点以 x 为根和所有叶子节点值的总和）。

2. 每个节点 t[x] 覆盖的长度为 lowbit(x) 。

3. 每个节点 t[x] 的父节点为 t[x + lowbit(x)] 。

4. 树的深度是$log_2n + 1$。

# 举个例子

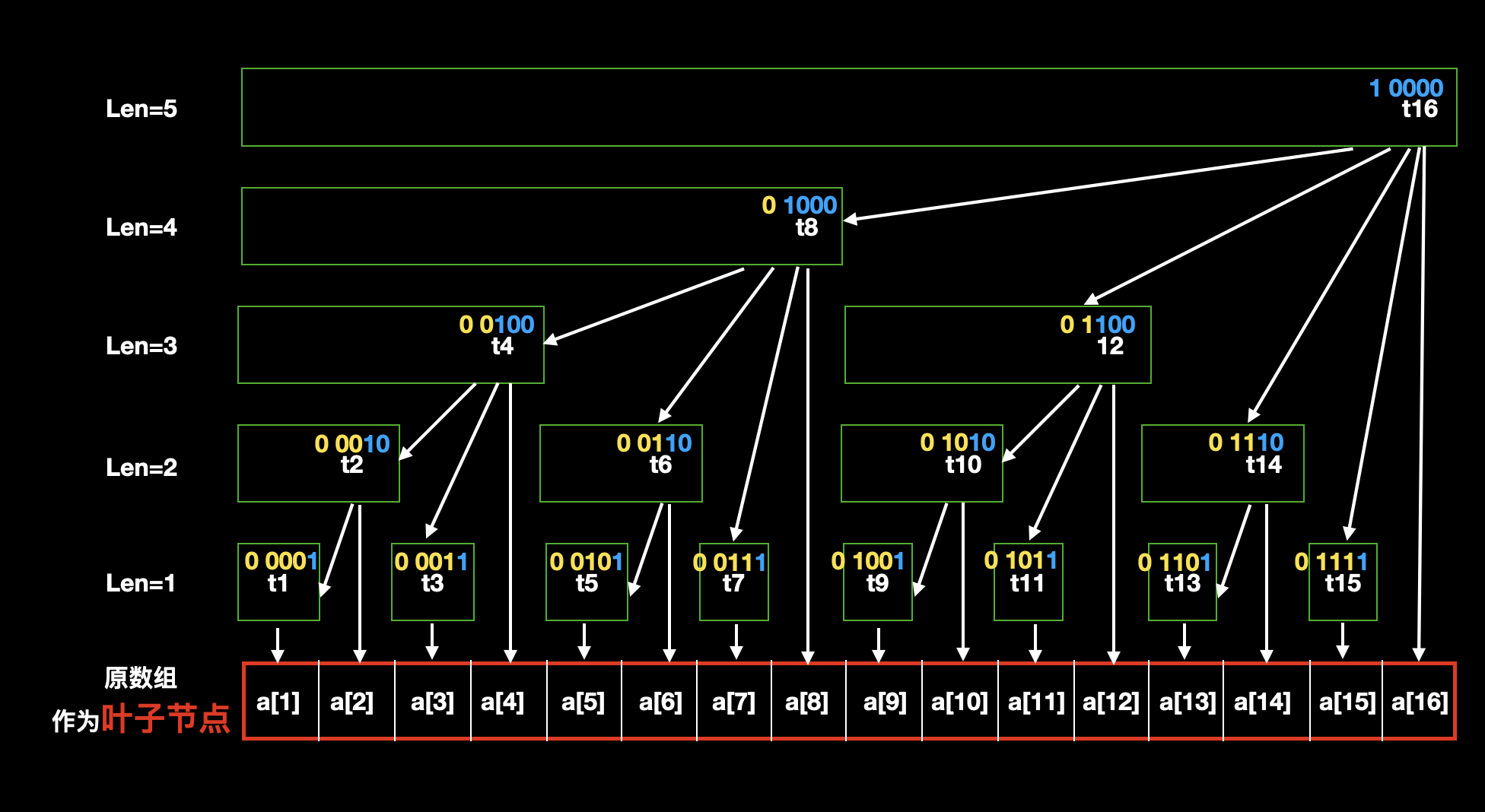
使用上述规则，生成一个 n=16 的树状数组。

图中，使用蓝色字体表示 lowbit [x] 的值，比如： t[8]=lowbit(8)=(二进制)1000=8 。因此 t[8] 覆盖了 8 个长度。并且 8+lowbit[8]=16 ，所以它的父节点是 t[16] 。

以 8 为根的子树的所有叶子节点分别是 1~8，我们计算它的值 只需要计算 t[4]+t[6]+t[7]+a[8] 。

因为 t[4] 已经算出了 1~4 的叶子节点的总和， t[6] 已经算出了 5~6 的叶子节点的总和，而 t[7] 是 a[7] 本身，再加上 a[8] ，如此就把 t[8] 算出出来了。

# 如何得到区间的长度？

在文章开始，我们提到了树状数组又叫二进制索引树，通过二进制来划分区间。

它实际的划分规则是：假如 t [x] 中 x 的二进制表示的末尾 有 k 个 连续的 0，则 t [x] 存储的区间长度为 $2^k$ ，也就是 最低位的 1 和它后面的 0 所构成的数值。存储的值是由 a [x] 向前数 $2^k$ 个元素之和。

我们以 t[12] 进行举例。 12 的二进制表示是 $(01100)_2$ ，它的末尾有两个连续的 0，那么 t[12] 就存储 $2^2=4$ 个数字之和，其实就是 最低位的 1 和它后面的 0 所构成的数值$(100)_2=4$。

这四个数字分别是 从 12 开始往前数 4 个 ，也就是 [9,10,11,12] 。

那么现在就出现了一个问题，我们如何从 x=12 的二进制表示 $(01100)_2$ 中取出 最后一个 1 和它后面所有的 0（也就是 $(100)_2$） 呢？

1. 先取反。取反就是把 1 变成 0，0 变成 1，那么 12 的二进制取反后就是 $(10011)_2$ 。

2. 再加 1。加 1 变成 $(10100)_2$ 。

3. 和原数字 做 “与” 运算，两位都是 1 结果为 1，否则为 0。也就是$(10100)_2 \& (01100)_2=(00100)_2$ 。

如此，我们就得出了区间的长度。

我们回过头来看下这三个步骤：

1. 步骤一和二加起来正好是一个 负数求补码的操作，也就是 -x 的补码正好是 x 先取反再加一。

2. 那么再加上第三步，就是 -x & x 。

我们神奇的发现，这正是 lowbit(x) 操作，所以我们可以用 lowbit(x) 来求出区间的长度。

计算机中二进制采用补码表示，正数的补码是原码本身，而负数的补码是反码加一。

# 直接前驱

前驱节点： t[x] 左侧的子树的根节点。

直接前驱节点： t[x] 左侧相邻的 子树的根节点。用公式表示是： t[x-lowbit(x)] 。

我们以 t[7] 为例， t[7] 的直接前驱是什么呢？

我们通过图中二进制表示（黄色 + 蓝色数字）我们可以直观的看到 lowbit(7) 的结果（蓝色数字）是$(1)_2$。那么 7-lowbit(7)=6 ，所以 t[6] 就是 t[7] 的直接前驱。以此类推，我们还能算出来 t[6] 的直接前驱就是 t[4] ，再算 t[4] 的直接前驱的时候发现是 0 ，寻找结束。

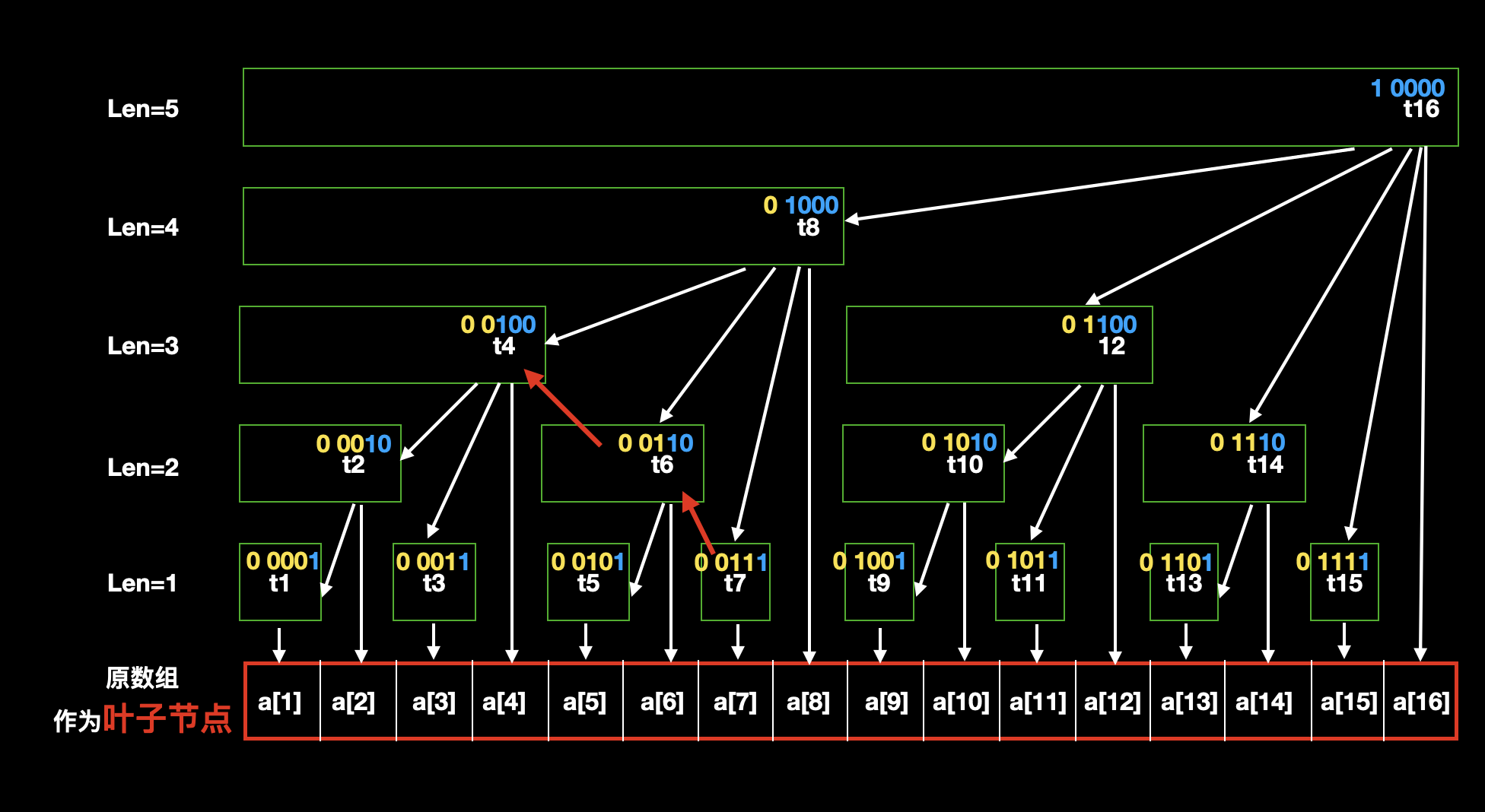
那么，通过搜索直接前驱节点，我们找到的是什么呢？

把他们加起来，很容易发现就是 7 的前缀和， t[4]+t[6]+t[7]=sum[7] ，我们用 sum 表示前缀和数组。

# 直接后继

后继节点： t[x] 的所有祖先。

直接后继节点： t[x] 的父节点。用公式表示是： t[x+lowbit(x)] 。

我们以 t[9] 为例，我们通过图中二进制表示（黄色 + 蓝色数字）我们可以直观的看到 lowbit(9) 的结果（蓝色数字）是$(1)_2$。那么 9+lowbit(9)=10 ，所以 t[10] 就是 t[9] 的父节点，以此类推，我们依次向上找父节点会发现 t[10] 的父节点是 t[12] ， t[12] 的父节点是 t[16] ，寻找结束。

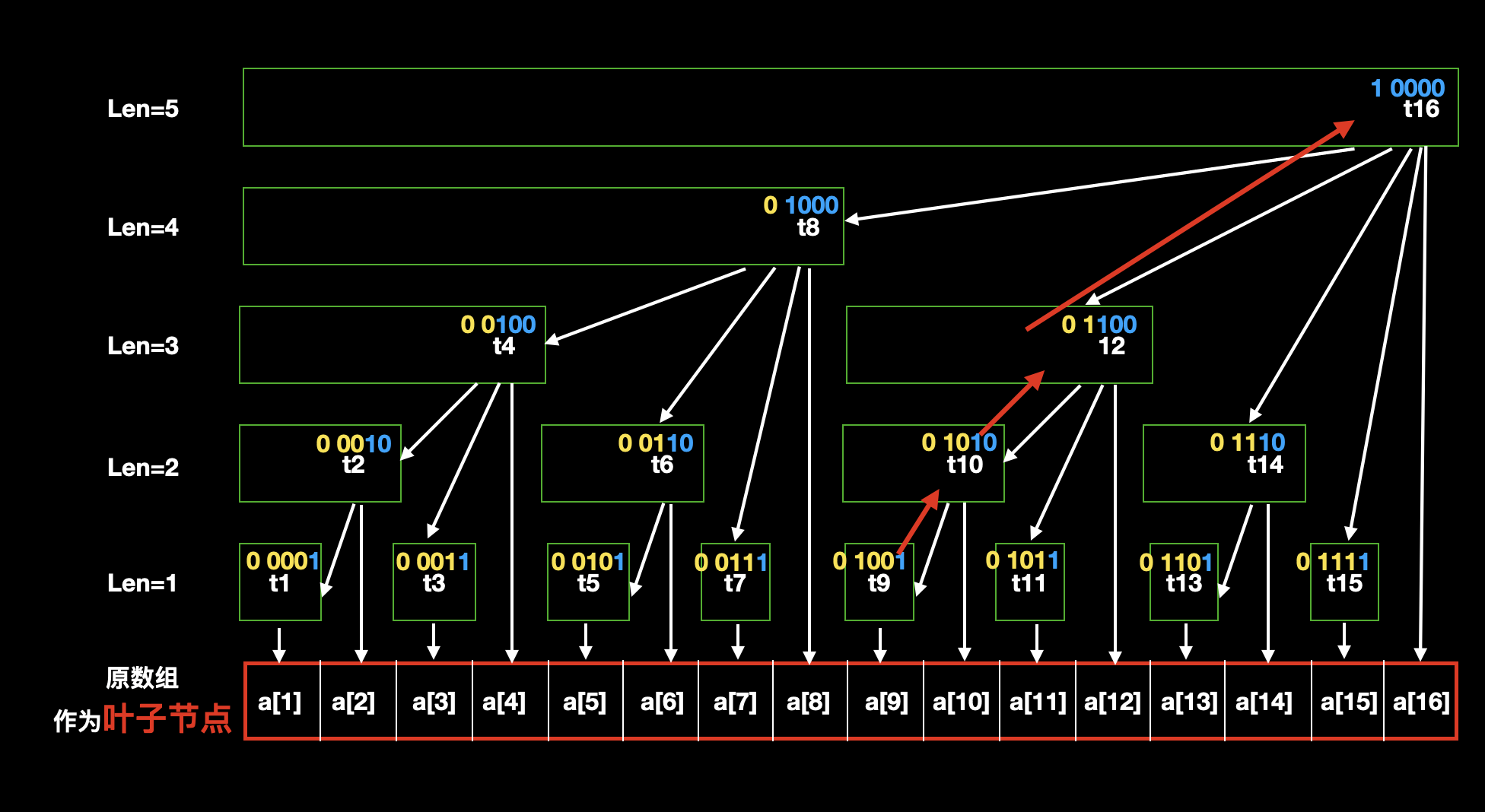
那么，通过搜索父节点，能起到什么作用呢？

观察图示，我们可以发现当我们搜索完 t [9] 和它的后继节点之后，我们找到了所有和 a [9] 相关的节点，假如我们要修改 a [9] 中的元素，就需要把这些相关节点一并修改，来维护树状数组的正确性。

# 操作：查询区间 [l,r] 中所有数字之和

理解前驱节点之后，其实区间查询就是普通的前缀和操作。查找区间 [L,R]，就可以使用前缀和数组计算： sum[R]-sum[L-1] 。而前缀和数组 sum[x] 的计算方式我们在前面已经知道了。

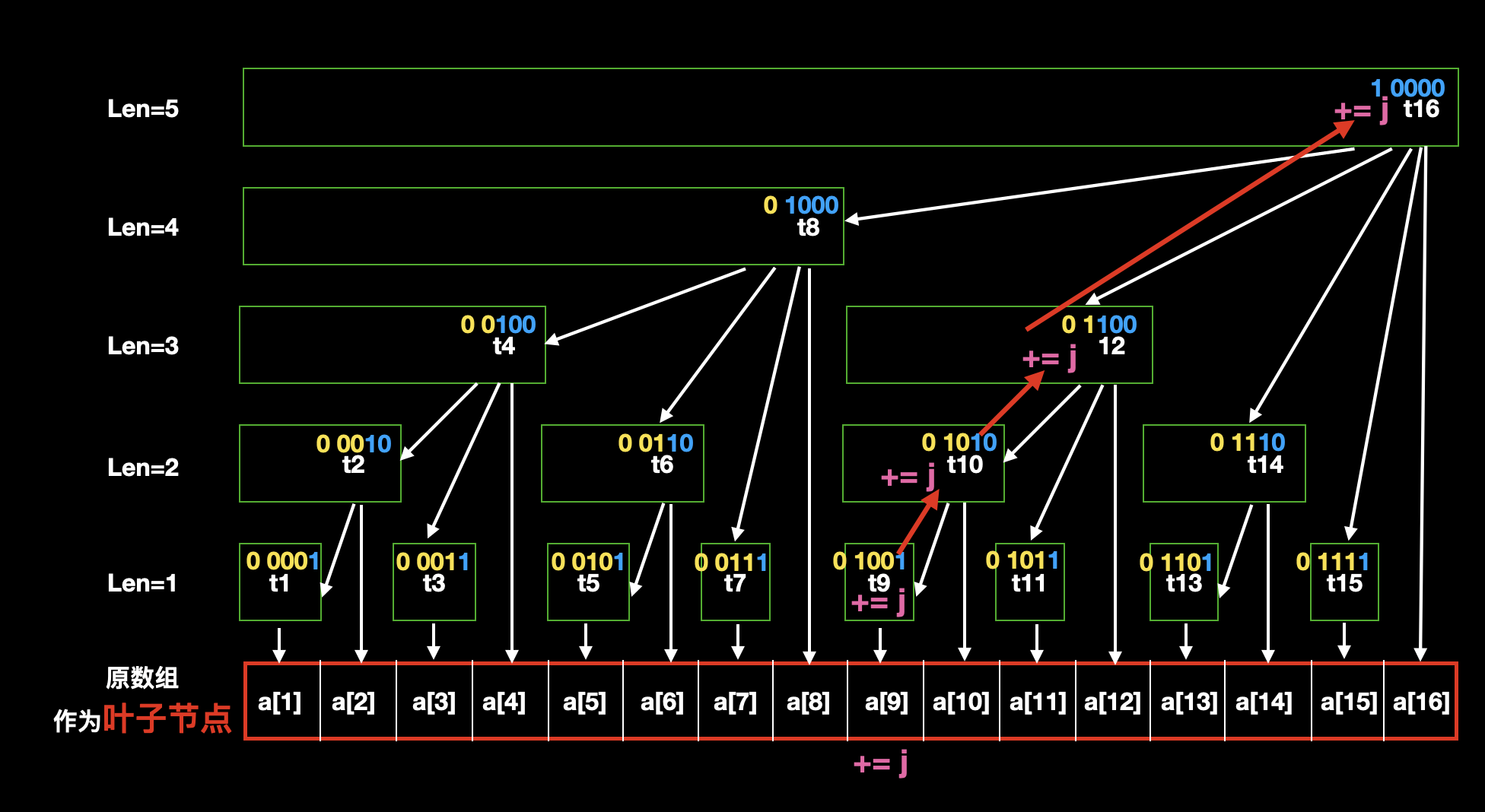
# 操作：在位置 i 上增加一个数 j

理解后继节点之后，我们就知道怎么做这个操作了，其实就是把所有与 i 相关的节点全部加上 j ，而怎么找所有与 i 相关的节点，我们在前面已经知道了。

# 实现

树状数组在实现上是非常简单的数据结构。

// 返回非负整数 x 在二进制表示下 最后一个 1 及其 后面的 0 构成的数值

int lowbit(int x) {

    return x & -x;

}

// 在位置 x 上，增加 k

void add(int x, int k) {

    // 每个父节点都加上 x + lowbit (x) 就是父节点

    for(int i = x; i <= n; i += lowbit(i)) t[i] += k;

}

// 查询前 x 个数的和

int ask(int x) {

    int res = 0;

    // 每次都减去直接前驱节点 也就是 x - lowbit (x)

    for(int i = x; i; i -= lowbit(i)) res += t[i];

    return res;

}

// 查询区间和 [L, R]

int ask(int L, int R) {

    return ask(R) - ask(L - 1);

}

# 时间复杂度和应用场景

在更新一个点的时候，从叶子节点更新到树根，那么高度就是树的高度，也就是 logn 。

前缀和查询的时候，从当前节点一直找前驱，同样最多找 logn 次。

所以，总的时间复杂度是$O(logn)$ 的。

从时间复杂度上，我们也能看出来树状数组的主要应用场景是 logn 的时间内，在点更新的同时，求前缀和。

END