这是一篇关于滑动窗口的详细的入门级攻略(真的就只是入门级)。
本文指 ACM 算法中的滑动窗口,而不是 TCP 拥塞控制中使用的滑动窗口协议(虽然两者十分相似)。
一定要看最后的总结呀~
# 滑动窗口的概念
滑动窗口算法是一种在数组中找到满足给定条件的子数组的方法,当然字符串也是适用的。我们通过维护一个子集作为窗口来做到这一点,并在更大的列表中调整和移动该窗口,直到找到解决方案。
# 从经典例题开始
# LeetCode 239. 滑动窗口最大值
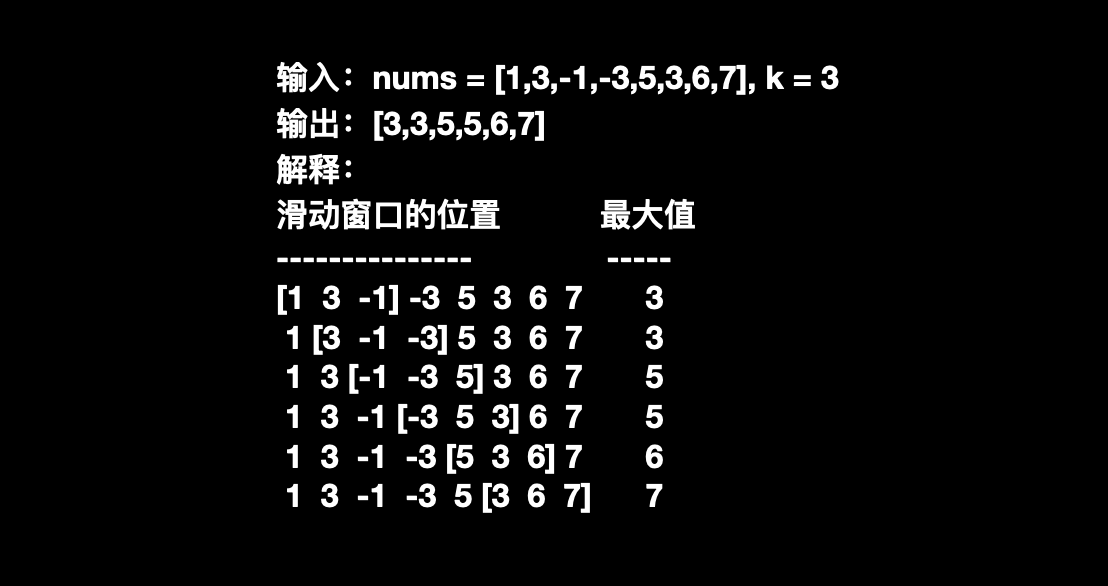
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
# 简单的思路
本题的题意是比较清楚的,因此不在赘述题意,不明白题意的话,可以结合示例理解一下。
首先看到题目,很容易想出来的思路是:两重嵌套循环,外循环遍历窗口,内循环遍历当前窗口的每一个数字,自然可以求出每一个窗口的最大值。
用伪代码表示该过程:
vector<int> res; | |
for (遍历每个窗口 i) { | |
t = INT_MIN; | |
for (遍历窗口中的每个数字 j) { | |
t = max(t, j); | |
} | |
res.push_back(t); | |
} |
分析一下代码,发现这种做法妥妥的是 O (nk) 的时间复杂度(其中 n 为 nums 长度)。而本题的数据范围中,n 和 k 都是 势必会超时。
那么,我们分析一下,这种暴力的做法是否有什么冗余呢?
很关键
首先,从示例中来看,我们要 求的是最大值,当窗口在 [-1,-3,5] 的时候,遍历窗口中的每个数字,求出 最大值5 之后,窗口向右移动一位来到 [-3,5,3] ,再次遍历窗口中的每个数字,求出最大值,仍然是 5 。
OK,请注意上述过程,我们在两次求最大值的时候,都遍历了窗口中的所有元素,所以两个窗口中的共同元素 -3 被遍历了两次。
而它 ( -3 ) 有必要被遍历到两次吗?没有必要,甚至它根本不需要再被遍历到。我们注意到它后面的数字 5 ,比它更大,并且在它之后滑出窗口,因此只要 5 存在, -3 就必然不可能是窗口中的最大值。
也就是说,只要比 -3 更大的数字 5 进入窗口, -3 根本就没有必要再被遍历了。
进一步的,你会发现当前窗口中所有比 5 小的数字,其实都不需要被遍历了,因为他们都在 5 之前滑出窗口,并且因为 5 的存在,他们都不可能是最大值。
综上,我们是否可以想到一种方式:用一个具有单调性的双端队列作为窗口,来存储遍历到的每个数字,我们让队列头部时刻保持最大值,这样每次直接取队头元素就是当前窗口的最大值。
很关键结束
# Code
思路虽然说理解起来并不难,但是想实现好,仍然需要诸多细节:
- 当前遍历到的元素 i 大于队尾元素的情况下,为了保持单调性,需要将队列中所有比 i 小的元素均弹出队列。
- 需要判断队头元素是否已经滑出了窗口。
- 什么时候开始输出元素。
为了解决第二点,我们让队列中存储下标,而不是值。这样我们通过下标来判断当前处于哪个窗口,而队列为了保持单调性,可能没有完整存储窗口中所有元素。
vector<int> maxSlidingWindow(vector<int>& nums, int k) { | |
vector<int> res; | |
deque<int> q; | |
for (int i = 0; i < nums.size(); i ++ ) { | |
// 代码①。只要队尾元素小于当前元素,就弹出队尾元素,保持队列单调性。 | |
while (!q.empty() && nums[q.back()] < nums[i]) { | |
q.pop_back(); | |
} | |
q.push_back(i); // 代码②。入队 | |
// 代码③。当队首元素滑出窗口,就把队首元素出队。 | |
if (!q.empty() && i - k >= q.front()) { | |
q.pop_front(); | |
} | |
// 代码④。窗口形成 才可以开始输出元素。 | |
if (i - k + 1 >= 0) { | |
res.push_back(nums[q.front()]); | |
} | |
} | |
return res; | |
} |
# 代码执行流程
如果读者还不能理解滑动窗口的含义,可以根据下图梳理一遍整个执行流程中队列的变换。
有几点需要注意:
- 判断队首元素是否滑出窗口,用了
i-k>=q.front(),请参考,当前下标k=3、i=7的时候,此时窗口中的元素下标应该是[5,6,7],那么i-k实际上就是当前窗口的最左边元素的前一个元素,我们判断如果这个元素大于等于队列头部元素 (直接等于也可以,因为一次只能滑动一步),则说明该头部元素已经滑出窗口,既,代码③。 - 判断窗口形成,用了
i-k+1>=0,也就是当i=2的时候,窗口刚好形成。 - 请根据代码执行流程来理解滑动窗口的设计思想。
![]()
# 时间复杂度
虽然,使用单调队列实现的滑动窗口也有两重循环,但是我们可以发现每个元素,只 进 出 队列一次,因此该实现是标准的线性时间复杂度,既 O (n)。
# LeetCode 3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释:因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:
输入: s = "bbbbb"
输出: 1
解释:因为无重复字符的最长子串是 "b",所以其长度为 1。示例 3:
输入: s = "pwwkew"
输出: 3
解释:因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
# 思路与实现
本题也是最经典的滑动窗口的应用之一。先来理解一下题目,本题有几个关键点:
- 子串的概念是:连续的字符串,不可以隔着选;
- 子串中的字符不能重复。
- 目标是找到 所有不重复字符子串 中 最长的那一个。
既然是连续的不重复子串,那么一个很容易想到的做法是:嵌套循环,外循环枚举每一个字符 i,内循环 i 处向后枚举每一个字符,内循环的字符如果和外循环的字符重复,则记录最大值,并 break。
用伪代码表示该过程:
int res = 0; // 最长的无重复字符子串 | |
for (遍历每个字符 i) | |
for (j: i+1 ~ n) | |
if (j = n - 1 || s[i] == s[j]) | |
res = max(res, j - i); | |
break; |
各位发现没有,这个伪代码怎么和上一题的长的有点像呢?那我们可不可以用相同的思路优化呢?
还是先来看一下这种暴力的做法有什么地方是冗余的操作。以示例 1 中 s = "abcabcbb" 为例。
当我们执行外循环,第一次枚举出 abca 的时候,我们得到了 res=3 ,此时,继续执行外循环,又枚举出了 bcab 。注意,实际上,我们在第一次枚举的时候,实际上已经得知了一个隐含信息,既,bca 是不重复的。
大家可以思考一下:当刚好枚举到第二个 a (注意这里的关键词是 "刚好") ,也就是子串 abca 的时候发生重复,那么说明什么?说明当去掉第一个 a 之后,剩下的子串 bca 是不重复的,可是我们继续循环的时候,仍然又枚举了 bca ,此时就出现了冗余操作。
(为了避免歧义,特别说明一下,在这个例子里,出现重复的 a 在子串最左边可能显得有点特殊,但是实际重复的字符可能出现在任何位置。)
如何优化呢?
我们就可以使用滑动窗口的技巧,维护一个没有重复字符的窗口,具体如何做呢?
可以使用双指针来解决,具体的:
- 一个指针 right 向后扫描字符串,使用哈希表记录每个字符出现的次数。
- 移动指针 left,直到重复的这个字符只出现一次为止。
- 更新结果。
# Code
实现上有两个小细节:
- 使用 hash 表来统计当前重复的字符;
- 因为在第二步已经保证了,没有重复字符,所以在更新结果的时候,直接更新
i~j的距离就行了,也就是j-i+1(注意不是伪代码中的j-i)。
int lengthOfLongestSubstring(string s) { | |
int res = 0; | |
unordered_map<char, int> h; | |
for (int i = 0, j = 0; j < s.size(); j ++ ) { | |
h[s[j]] ++ ; // 统计当前字符的出现次数 | |
// 当前字符如果重复出现,就移动左指针,直到不重复 | |
while (h[s[j]] > 1) h[s[i ++ ]] -- ; | |
res = max(res, j - i + 1); // 统计结果 | |
} | |
return res; |
# 小结
从上面两个例题中,可以看出滑动窗口并不是某个指定的算法,而是一种解题思路(或者说技巧),用来处理某类固定的问题。根据问题的不同选用不同的实现方式,比如:第一题使用了单调队列实现、而第二题则使用了双指针实现。
# 更多的练习题
# LeetCode 76. 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
- 如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
# 实现与分析
本题也是滑动窗口的经典应用,是一个很关键的例题。
首先看一下题意,题目有中有几个关键点:
- s 和 t 中均有重复字符,那么对于 t 中的重复字符 x,找到的 s 子串中 x 的数量不能比 t 中少。
- 子串必须是连续的。
- 很重要的一点是,对于 t 中的每个字符,在 s 子串中的相对位置可以不同。
本题其实是一个经典的滑动窗口应用,并且窗口的长度是可变的。
按照前面一道题(无重复字符的最长子串)的思路分析,我们的算法可以分为以下步骤:
- 用
哈希表ht统计t中每个字符的个数,用一个整形cnt来统计当前已经匹配的字符个数; - 用双指针
i和j组成窗口,扫描整个s串,用另一个哈希表hs来统计当前扫描到的 s 中的字符s[i]的个数; - 如果 s 串中的字符也在 t 串中,同时个数不多余 t 串中的字符个数,那就说明该字符是有用的,把
cnt++,表示找到了一个有用的字符。 - 检查 s [j] 是否多余,如果多余,则向后移动;
- 判断 cnt 是否于 t 的大小相等,如果是,则更新答案;
# Code
string minWindow(string s, string t) { | |
unordered_map<char, int> ht, hs; | |
int cnt = 0; | |
string res; | |
// 统计 t 中每个字符的个数 | |
for (int i = 0; i < t.size(); i ++ ) ht[t[i]] ++ ; | |
// 双指针形成窗口,扫描 字符串 s | |
for (int i = 0, j = 0; i < s.size(); i ++ ) { | |
hs[s[i]] ++ ; // 统计字符 s [i] 个数 | |
// 有效字符可以使 cnt ++ | |
if (hs[s[i]] <= ht[s[i]]) cnt ++ ; | |
// 通过移动指针 j 来过滤掉多余字符 | |
while (j <= i && hs[s[j]] > ht[s[j]]) { | |
hs[s[j ++ ]] -- ; | |
} | |
// 如果有效字符和 t 中字符数量相等,则更新答案 | |
if (cnt == t.size()) { | |
if (res.empty() || i - j + 1 < res.size()) { | |
res = s.substr(j, i - j + 1); | |
} | |
} | |
} | |
return res; | |
} |
# 一些你可能有的疑问
为什么仅仅靠 cnt 和 t 中字符数量相等,就可以认定是找到了有效子串呢?不会出现(s 的子串中)某个字符多导致了另外的字符少这种情况吗?
答:不会的,注意代码的顺序,我们在步骤 4 中过滤了多余的字符,使得当前扫描过的所有 s [i] 的数量一定小于等于它在 t 中的数量,这也是指针 j 存在的意义。这就使得到达步骤 5 的时候,cnt 只有两种情况:1、小于 t 中字符数量;2、等于 t 中字符数量;
cnt 的变化。
请注意,cnt 只有一种情况会变化,它只会被指针 i 控制,只有在当前 s [i] 是有效字符的时候,才会变化,并且只增不减。那么,它会不会超过 t 的大小,从而使靠后的合法结果没办法统计到呢?不会的,因为当 cnt 等于 t 的大小时,说明所有的有效字符已经找全了,这些已经找全的字符不会再减少了,因为步骤 4 我们只会过滤多余的字符,而已经找到的合法字符不会减少,所以所以当 cnt 第一次等于 t 大小的时候,cnt 的值就固定下来,不会在变化了。
如何去定义(s 中的)有效字符?
答:在上述的代码实现中,我们认为(s 中的)有效字符必须满足以下两点:1、在 t 中存在;2、hs 中统计到的数量,没有超过该字符在 ht 中统计的数量。
如何定义冗余字符?
答:在上述的代码实现中,我们认为某个有效字符的数量不满足它的第二点,则新统计到的有效字符就是冗余的,需要过滤掉。
步骤 4 过滤冗余字符,会不会同时把有效字符也过滤掉?
答:不会的,因为过滤字符是操作是在哈希表中减少它的数量,而不是在滑动窗口中把它移动出去。
滑动窗口里面存的到底是什么?
答:滑动窗口 (j~i) 存的有效内容是 包含 t 中所有字符的 s 子串。比如:示例中的
ADOBEC、BANC。i 和 j 的作用是什么?或者说 为啥要用滑动窗口?
答:指针 i 负责统计 s [i] 的个数,并且统计有效字符,也就是更新 cnt。指针 j 负责将冗余的 s [i] 去掉,以保证能得到题目要求的 "最小覆盖子串"。
如果还有不懂的问题,请直接把示例给的数据带入到代码中,在脑海里完整执行一遍叭。
# LeetCode 424. 替换后的最长重复字符
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。
在执行上述操作后,返回包含相同字母的最长子字符串的长度。
示例 1:
输入:s = "ABAB", k = 2
输出:4输入:s = "AABABBA", k = 1
输出:4
解释:
将中间的一个 'A' 替换为 'B', 字符串变为 "AABBBBA"。子串 "BBBB" 有最长重复字母,答案为 4。
# 思路及实现
本题的题意比较简单,可以将给定的字符串 s 中的字符任意修改 k 个,然后问修改之后可以得到的包含相同字符的最长子串的长度(最终目标)。
本题有一个重要的关键点,那就是修改哪些字符可以达到最终目标?
要理解这点,必须转明白一个脑筋急转弯:想通过修改让一个子串的字符全相同,那么子串中出现次数最多的字符一定是不用修改的,而修改的一定是其他字符。
也就是说只要找出这个子串中出现次数最多的字符的个数 x,然后用这个子串的长度减去 x,就是我需要修改的字符个数。
更进一步的思考,如果我们用一个滑动窗口来保存可以通过修改 k 个字符,达到全部字符相同的子串,那么我们只要在这些子串中找到长度最长的那个就可以了。
具体地:
- 使用双指针来维护滑动窗口。枚举字符串 s,用
哈希表h统计当前字符 s [i] 出现的次数,并且更新当前出现最多字符的次数 maxx; - 移动指针 j 以保证当前子串想要统一字符,需要修改的字符个数不大于 k;
- 更新结果;
# Code
int characterReplacement(string s, int k) { | |
unordered_map<char, int> h; | |
int maxx = 0; | |
int res; | |
for (int i = 0, j = 0; i < s.size(); i ++ ) { | |
h[s[i]] ++ ; // 统计当前字符个数 | |
maxx = max(h[s[i]], maxx); // 更新当前最多字符个数 | |
// 步骤二 | |
while (i - j + 1 - maxx > k) { | |
//s [j] 滑出窗口 因此个数减少 | |
h[s[j]] -- ; | |
// 下面要先更新当前最多字符个数,再移动 j | |
// 不然就更新错字符了。 | |
maxx = max(h[s[j]], maxx); | |
j ++ ; | |
} | |
res = max(i - j + 1, res); | |
} | |
return res; | |
} |
# 需要注意的地方
- 每次出现字符数量的变更,都可能影响 当前最多字符个数,因此两者必须前后同步变更;
- 所以在移动指针 j 的时候,也需要先更新当前最多字符个数,再移动。
- 当前滑动窗口中的字符总共是
i-j+1。
# LeetCode 1438. 绝对差不超过限制的最长连续子数组
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
示例 1:
输入:nums = [8,2,4,7], limit = 4
输出:2
解释:所有子数组如下:
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4.
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4.
因此,满足题意的最长子数组的长度为 2 。
# 思路及实现
本题有一个比较重要的概念:最大绝对差的含义是区间内最大值和最小值的差值。
我们的最终目标是:找到最大绝对差不大于 limit 的最大区间长度。
那么这题如何使用滑动窗口解决呢?
我们可以用滑动窗口,来保证窗口内的所有元素 最大绝对值差 不大于 limit。只要大于 limit,就向后移动窗口。
那么如何知道窗口内的最大值和最小值呢?细心的同学可能已经发现了,这不就是第一道题(滑动窗口的最大值)吗?如果不理解,同学们可以再复习一下第一道题。
在第一道题里面,我们用一个单调队列来存储枚举到的数字,那么队列头部自然就是最大值。放到这道题里面,我们也可以这样做,只不过本题需要使用两个单调队列一个单调递减存放最大值,一个单调递增存放最小值,这样我们就能在 O (1) 时间复杂度内判断出 最大绝对差 。
# Code
int longestSubarray(vector<int>& nums, int limit) { | |
deque<int> minq; // 单调递增队列,队首是最小值 | |
deque<int> maxq; // 单调递减队列,队首是最大值 | |
int res = 0; // 存储最终结果。 | |
for (int i = 0, j = 0; i < nums.size(); i ++ ) { | |
// 保证两个队列的单调性 | |
while (!minq.empty() && nums[i] < minq.back()) minq.pop_back(); | |
while (!maxq.empty() && nums[i] > maxq.back()) maxq.pop_back(); | |
// 把遍历的数字同时加入两个队列 | |
minq.push_back(nums[i]); | |
maxq.push_back(nums[i]); | |
// 当前窗口不满足条件 | |
while (!minq.empty() && !maxq.empty() && maxq.front() - minq.front() > limit) { | |
// 窗口向右移动,不在窗口中的数字,也要从队列中踢出。 | |
if (nums[j] == minq.front()) minq.pop_front(); | |
if (nums[j] == maxq.front()) maxq.pop_front(); | |
j ++ ; | |
} | |
res = max(res, i - j + 1); // 更新结果 | |
} | |
return res; | |
} |
本题有点像是前面几道题思路的融合,既用到了双指针来控制大小不固定的滑动窗口,又用到了单调队列来存储窗口中的极值。
# 总结
如果同学们能按照顺序看到现在,并且亲自做了本文提供的五道题目,那么,大家应该对 “滑动窗口” 有了一定的了解。所以我们可以通过这几道题目总结一下,什么时候可以使用滑动窗口,以及如何实现滑动窗口。
什么时候可以使用滑动窗口?
从本文的几道题来看,它们具有一个明显的共性,既,具有连续性。这点在题目中均有提示,第一道题自不必说,第二三四题在题目中标明求子字符串,而子字符串必须是连续的,第五题的题面也说明了求连续子数组。
并且另一个不算明显的共性是,最终目标都是求极值,也就是最大值或最小值,而不用真的求出具体的字符串或者数组。
综上,在具有连续性的字符串或数组问题上,并且最终答案只需要求极值的问题上,我们可以优先考虑是否可以用滑动窗口。
滑动窗口应该怎么实现比较好呢?
其实滑动窗口并没有什么固定的套路,但是从本文的几道题目来看,比较常用的方式是使用双指针来实现,并且辅以单调队列来存储极值,或者辅以哈希表来存储个数。可以粗略的参考下面的伪代码,根据题目灵活运用。
伪代码 res;q;h;for (i, j: 序列) {
while (保证队列单调) q.pop_back();
q.push_back(i);
h[s[i]] ++ ;
// 根据题目要求进行操作// 在不满足条件的情况下,移动窗口j ++ ;
// 如果使用了队列,那么不在窗口中的元素要从队列头部出队。// 如果使用哈希表技术,那么不在窗口的元素的计数要减一 。// 更新结果。res = max(res, i - j + 1);
}这里面其实还涉及到一个问题,既,窗口的大小用
i-j+1来表示,这是因为我们是从 0 开始枚举的序列下标,例如:如果当前i=2,j=0,那么当前窗口大小就是3,也就是i-j+1。
END