# 前置知识
初始版本是这个:神奇的线段树(上),初始版本中的攻略并不完全,没有懒标记部分,因此在本文(2.0 版本)中,将更新更详细的讲解,以及时间复杂度的证明,补充懒标记部分。
# 线段树
线段树是一种基于分治思想的二叉树结构,用于在区间上进行信息统计。
# 那么线段树长什么样子呢?
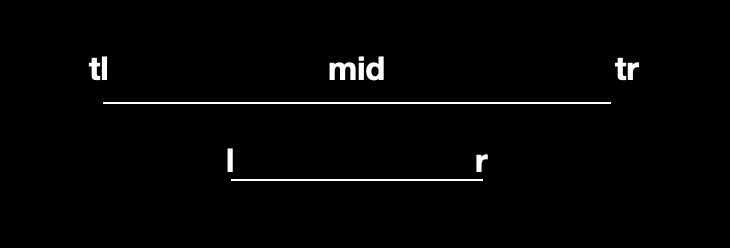
- 线段树上的每一个节点都代表着一个区间;
- 线段树的根节点代表着最大的统计范围;
- 线段树的每一个叶结点的长度都是 1,也就是唯一值;
- 对于每个内部节点
[L,R],它的左子节点都是[L,mid],右子节点都是[mid+1,R],其中mid的值为mid=(L+R)/2(向下取整)。
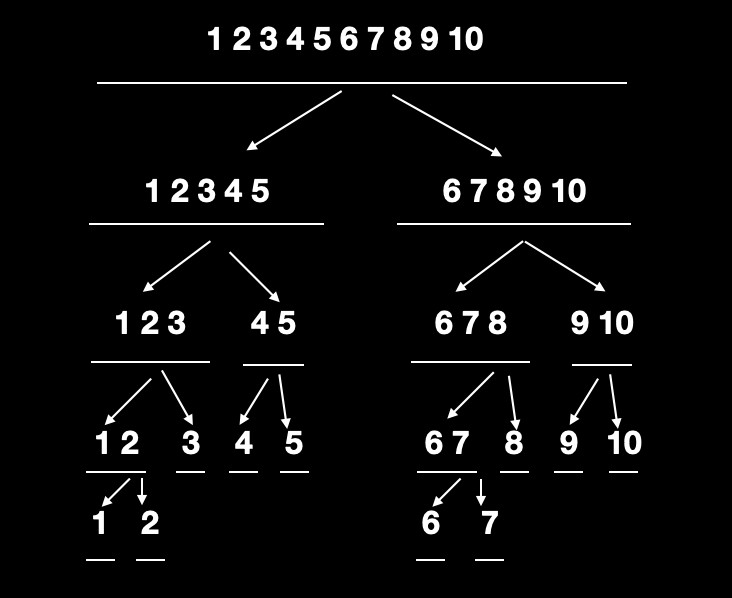
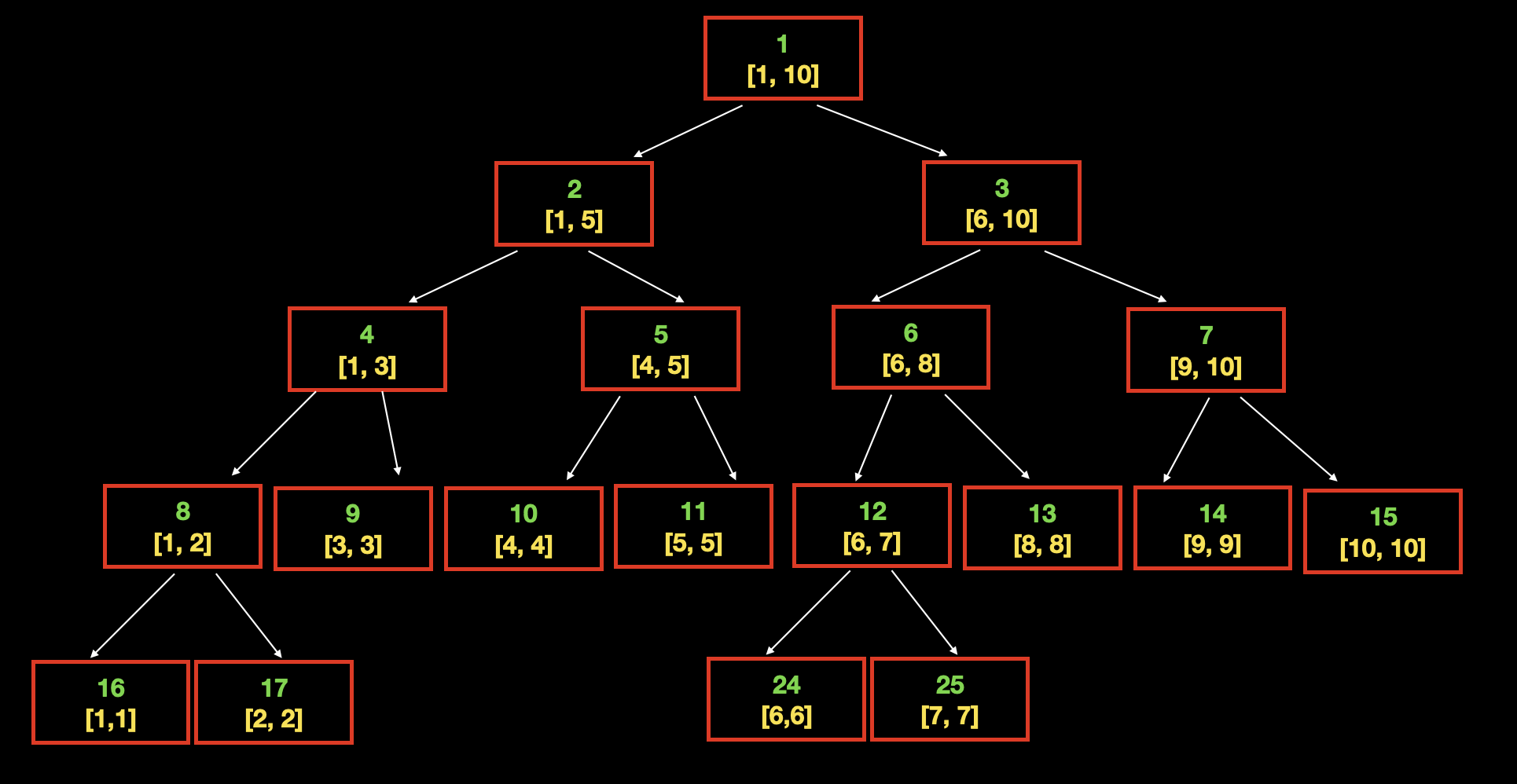
从图中可以看出来,线段树的存储就是标准二叉树的存储方法。
二叉树的一维数组存储:
- 根节点的编号为 1;
- 对于节点 x,它的父节点为 x/2;
- 它的左子节点为 2x;
- 它的右子节点为 2x+1;
# 线段树的基本操作
# 由两个子节点计算根节点(push_up)
需要根据线段树中节点的信息来计算,因此,需要根据不同的题意,具体问题具体分析。
# 由根节点计算两个子节点(push_down)
该操作比较复杂,因此放在下篇文章中来讲。
# 建立线段树(Build)
建立线段树很好理解,分为以下几个步骤:
- 存储当前节点的左右儿子;
- 如果当前节点的左右儿子相等,说明走到了一个叶子节点,结束递归即可;
- 计算 mid,注意这里一定要向下取整;
- 递归 左 右子节点;
- 最关键的一个步骤,
push_up(u);,其中 u 是当前节点。
void build(int u, int l, int r) { | |
// 存储当前左右节点到数组; | |
tree[u].l = l, tree[u].r = r; | |
// 找到叶子结点,结束递归; | |
if (l == r) return ; | |
// 计算 mid,注意向下取整; | |
int mid = (l + r) / 2; | |
// 递归左右节点; | |
build(u * 2, l, mid); | |
build(u * 2 + 1, mid + 1, r); | |
// 关键步骤 push_up | |
push_up(u); | |
} |
# 查询(Query)
假如,问题是求一段区间 [5,9] 的最大值,那么,我们线段数节点 存储的信息 就是 每个区间的最大值。
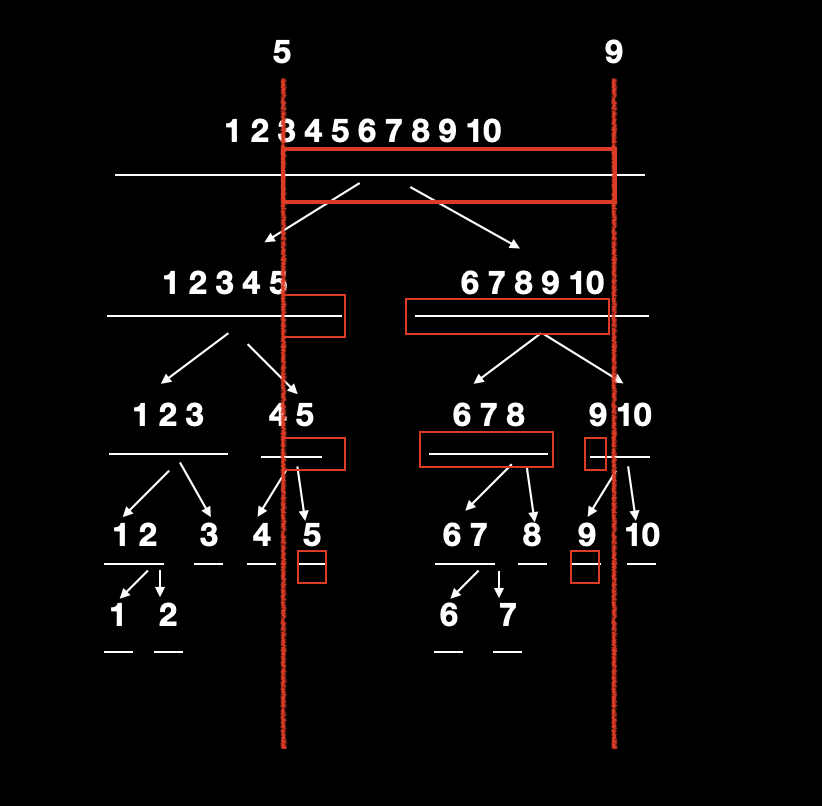
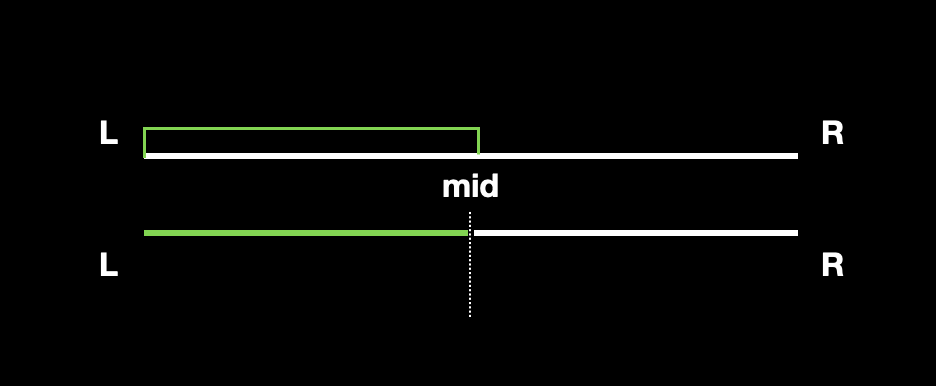
假设,使用 [L,R] 表示查询的区间,用 [Tl,Tr] 表示线段树中,当前搜索的区间,那么查询区间与当前搜索区间可能有下面的情况:
查询区间完全包含了当前搜索区间,说明我们已经找到了查询区间。
查询区间在当前搜索区间的右边,也就是
Tl <= L <= Tr <= R。![]()
此时,需要查看mid的位置来进行讨论如果
L>mid,则只需要递归右面[mid+1, R];如果
L<=mid,则需要递归左右两面,因为我们在建立线段树的时候,是根据 mid 来创建分支 (子树) 的。这里还有一个关键点,那就是虽然会有递归两边的情况。但是因为右边
[L,mid]在下一次递归中就已经完全在查询区间内部,变成了情况 1,所以右边只会被递归一次,不会对时间复杂度整体造成影响。
查询区间在当前搜索区间的左边,与情况 2 是完全对称的操作,因此不再赘述。
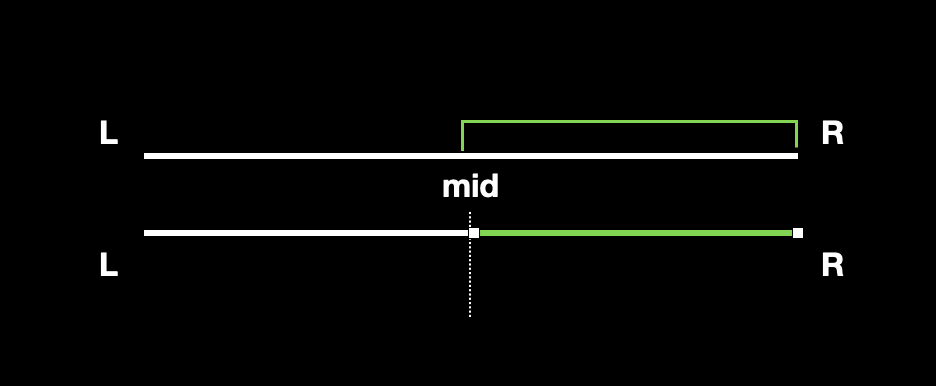
查询区间完全在当前搜索区间内部。
![]()
此时,也需要根据mid的位置来进行讨论:如果
R<=mid,则只需要递归左边[L, mid];如果
L>mid,则只需要递归右边[mid+1, R];mid在[L,R]中间,则需要递归两边,这就需要考虑到一个问题,递归两边会不会影响整体复杂度呢?其实是不会的,我们观察这种情况下递归左右两面之后,查询区间就完全包含当前区间(递归后,左当前区间是[L,mid],右当前区间是[mid+1,R],它俩组成整个查询区间)。也就是变成了情况 1,所以这种情况也只会分裂一次,因此不会影响整体复杂度。
# 修改(Modify)
修改操作与查询非常类似,可以说是查询的简单版,因此这里就不过多赘述,在应用代码中会详细注释。
# AcWing 1275. 最大数
给定一个正整数数列 a1,a2,…,an,每一个数都在 0∼p−1 之间。
可以对这列数进行两种操作:
- 添加操作:向序列后添加一个数,序列长度变成 n+1;
- 询问操作:询问这个序列中最后 L 个数中最大的数是多少。
程序运行的最开始,整数序列为空。一共要对整数序列进行 m 次操作。
写一个程序,读入操作的序列,并输出询问操作的答案。
输入格式
第一行有两个正整数 m,p,意义如题目描述;
接下来 m 行,每一行表示一个操作。
如果该行的内容是 Q L,则表示这个操作是询问序列中最后 L 个数的最大数是多少;
如果是 A t,则表示向序列后面加一个数,加入的数是 (t+a) mod p。其中,t 是输入的参数,a 是在这个添加操作之前最后一个询问操作的答案(如果之前没有询问操作,则 a=0)。
第一个操作一定是添加操作。对于询问操作,L>0 且不超过当前序列的长度。
输出格式
对于每一个询问操作,输出一行。该行只有一个数,即序列中最后 L 个数的最大数。
数据范围
1≤m≤2×10^5, 1≤p≤2×10^9, 0≤t < p输入样例
10 100 A 97 Q 1 Q 1 A 17 Q 2 A 63 Q 1 Q 1 Q 3 A 99输出样例
97 97 97 60 60 97样例解释
最后的序列是 97,14,60,96。
# 题目分析
题意清晰明了。
给出一个长度为 n 的序列,每个数在 0~p-1 之间。有两个操作:
- 单点修改:在区间中添加一个数(添加到末尾);
- 查询:某个区间内的最大值(从 L 到末尾
[L, n]);
# 题目描述
本题属于比较裸的可以用线段树解决的题目,主要是用本题熟悉一下线段树的实战应用。
# Code
#include <cstdio> | |
#include <algorithm> | |
#include <cstring> | |
#include <iostream> | |
using namespace std; | |
const int N = 200010; | |
int m, p; | |
struct Node { | |
int l, r; | |
// 节点中存储用来计算的信息。 | |
// 根据题意,本题需要存储 区间 [l, r] 中的最大值。 | |
int v; | |
}tree[N * 4]; | |
// 子节点信息计算父节点信息 | |
void pushup(int u) { | |
tree[u].v = max(tree[u * 2].v, tree[u * 2 + 1].v); | |
} | |
void build(int u, int l, int r) { | |
tree[u] = {l, r}; | |
if (l == r) return ; | |
int mid = l + r >> 1; | |
build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r); | |
// 注意 这里因为本题默认最大值是 0 所以初始化时候 每个节点最大值也都是 0 | |
//pushup (u); 所以这里不需要 pushup | |
} | |
int query(int u, int l, int r) { | |
// 查询区间 已经在 当前搜索区间 内 则返回结果 | |
if (tree[u].l >= l and tree[u].r <= r) return tree[u].v; | |
int mid = tree[u].l + tree[u].r >> 1; | |
int res = 0; | |
// 左边有交集 递归左边 递归时候查询区间不变 节点编号改变即可 | |
if (l <= mid) res = query(u * 2, l, r); | |
// 右边有交集 递归右边 并维护最大值 | |
if (r > mid) res = max(res, query(u * 2 + 1, l, r)); | |
return res; | |
} | |
// 修改从叶子节点开始修改 最后使用 pushup 操作向上更新 | |
//u 为当前节点编号 x 为叶子节点边界 [x, x] v 是更新后的最大值 | |
void modify(int u, int x, int v) { | |
// 找到对应的叶子节点 则更新 | |
if (tree[u].l == x and tree[u].r == x) tree[u].v = v; | |
else { | |
// 否则更新左面 或者 右面 | |
// 注意这里的左右必有一个更新 (与查询不同的地方) | |
// 这样才能 递归到叶子节点 | |
int mid = tree[u].l + tree[u].r >> 1; | |
if (x <= mid) modify(u * 2, x, v); // 递归左面 | |
else modify(u * 2 + 1, x, v); // 递归右面 | |
pushup(u); // 从叶子节点 向上更新 | |
} | |
} | |
int main() { | |
// 因为添加的数是上次查询的 所以还要存一下上次查询的结果 | |
int n = 0, last = 0; | |
scanf("%d%d", &m, &p); | |
//// 建树 A 操作增加节点 最大操作数量是 m 所以最大节点数量也是 m | |
build(1, 1, m); | |
char op[2]; | |
int x; | |
while (m -- ) { | |
scanf("%s%d", op, &x); | |
if (*op == 'Q') { | |
// 查询区间的范围 是最后 x 个数 也就是 [n-x+1, n] | |
last = query(1, n - x + 1, n); | |
printf("%d\n", last); | |
} else { | |
// 修改 既在末尾增加节点 | |
modify(1, n + 1, ((long long)last + x) % p); | |
n ++ ; | |
} | |
} | |
return 0; | |
} |
# AcWing 245. 你能回答这些问题吗
给定长度为 N 的数列 A,以及 M 条指令,每条指令可能是以下两种之一:
1 x y,查询区间 [x,y] 中的最大连续子段和,即 。2 x y,把 A [x] 改成 y。
对于每个查询指令,输出一个整数表示答案。输入格式
第一行两个整数 N,M。
第二行 N 个整数 A [i]。
接下来 M 行每行 3 个整数 k,x,y,k=1 表示查询(此时如果 x>y,请交换 x,y),k=2 表示修改。
输出格式
对于每个查询指令输出一个整数表示答案。
每个答案占一行。
数据范围
N≤500000,M≤100000, −1000≤A[i]≤1000输入样例
5 3 1 2 -3 4 5 1 2 3 2 2 -1 1 3 2输出样例
2 -1
# 题目描述
本题的题意也是比较清晰的。
给出一个长度为 N 的数列,以及两种操作:
- 查询操作:查询一个区间的最大连续子段和;
- 单点修改:把区间中的一个数 A [i] 修改成 y;
那么这里,就不得不解释一下最大连续子段和这个概念啦。
从给出公式中我们可以看出,其实就是整个区间中 ‘和’最大的 连续子区间的 ‘和’是多少。
# 题目分析
与上题相比,只是本题需要维护的属性变成最大的连续子段和。所以,我们如果知道如何维护这个属性,那么只要按照线段树的模板(类似上题的代码),就可以求出本题了。
# 用分治思想求最大连续子段和
如何分治呢?
假设,我们要求 [1,n] 的最大连续子段和,那么我们就可以把这个区间从中间一分为二,分成两部分:
- 中间值是
mid=(1+n)/2; - 左边的子区间就是
[1, mid]; - 右边的子区间就是
[mid+1, n]。
我们按照这种思路,一直递归下去,直到 节点只有一个元素 为止,也就是线段树中的叶子节点。
因为叶子节点只有一个元素,所以我们就得到了它的最大连续子段和,也就是这个元素本身。
现在,我们已经求出了最小区间的最大连续子段和,只需要向上回溯,通过已知的 子节点属性 求出 父节点属性。
所以现在问题变成了知道 左、右 两个子节点的 最大连续子段和 ,如何求它俩的父节点的呢?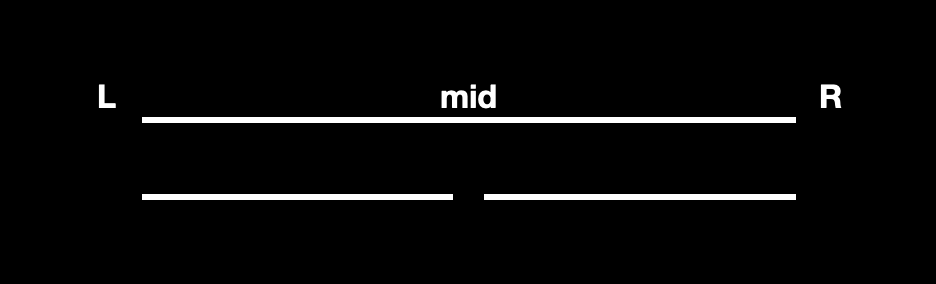
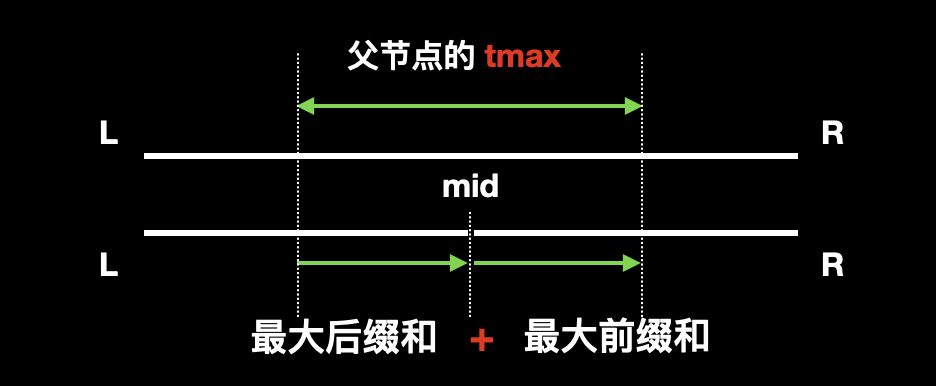
假设用 tmax 表示父节点的最大连续子段和,那么父节点的 tmax 只能处于下面三种情况,所以我们把这三种情况取最大值就是父节点的 tmax:
父节点的
tmax就在区间[L,mid]之中。这种情况下,自然父节点的tmax就等于左子节点的tmax;![]()
父节点的
tmax就在区间[mid+1, R]之中。这种情况下,自然父节点的tmax就等于右子节点的tmax;![]()
父节点的
tmax并不只在左右子区间,而是横跨两个区间。这种情况我们可以用左子区间(以 mid 作为最后元素)的最大后缀和 加上 右子区间(以 mid+1 作为起始元素)的最大前缀和。![]()
分析到这里,我们发现还要额外在节点内维护最大前缀和 Lmax 与最大后缀和 Rmax。
关于这两个属性,我们仍然分情况讨论:
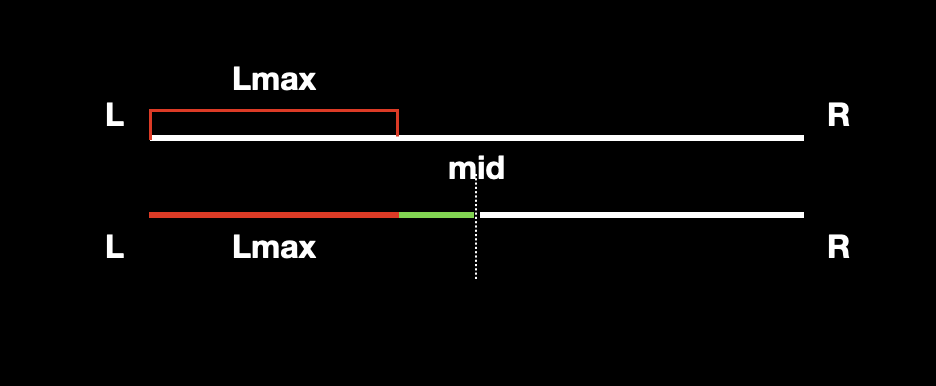
最大前缀和 Lmax:以左端点为起始元素的最大子段和。
通过左 / 右子节点 求父节点的 Lmax,则会出现两种情况,我们取两种中的最大值:
父节点的 Lmax 就在区间
[L,mid]之中,那么显然父节点的Lmax就等于左子区间的Lmax;![]()
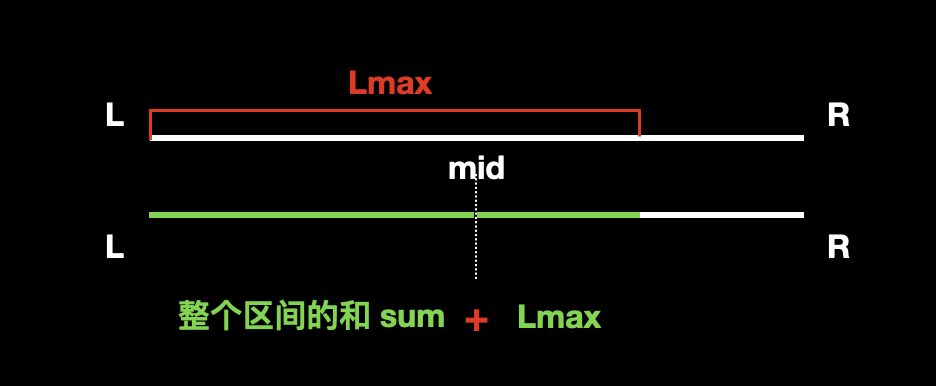
父节点的 Lmax 在区间
[L,R]之中,则需要用整个左子区间的和 加上 右子区间的 Lmax。![]()
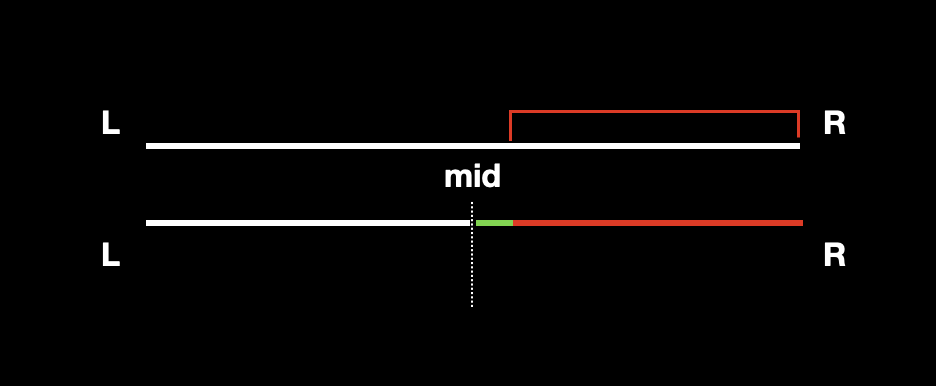
最大后缀和 Rmax:以右端点为结束元素的最大子段和。
通过左 / 右子节点 求父节点的 Rmax,同样会出现两种情况,我们取两种情况的最大值:
父节点的 Rmax 就在区间
[mid+1,R]之中,那么显然父节点的Rmax就等于右子区间的Rmax;![]()
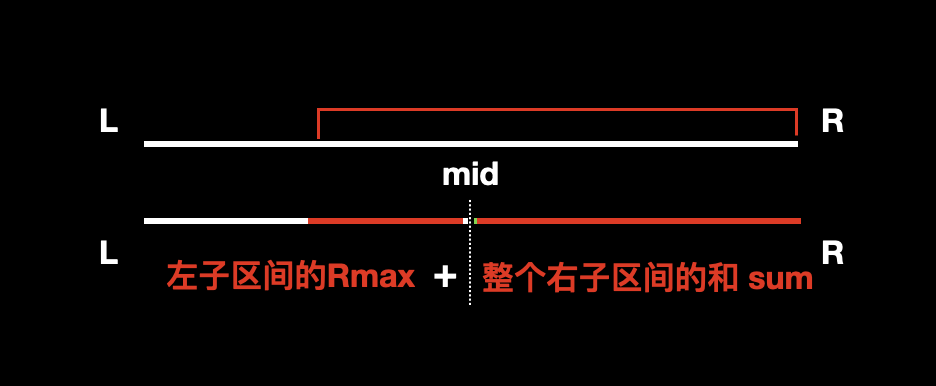
父节点的 Rmax 在区间
[L,R]之中,则需要用左子区间的 Rmax 加上 整个右子区间。![]()
分析到这里,我们发现只要在维护一个区间和就可以了。
而父节点的区间和 sum 就是 左子区间和 加上 右子区间和。
# Code
#include <cstdio> | |
#include <cstring> | |
#include <algorithm> | |
#include <iostream> | |
using namespace std; | |
const int N = 500010; | |
int n, m; | |
int w[N]; | |
struct Node { | |
int l, r; | |
// 节点中维护的四个属性:区间和,区间前缀和,区间后缀和,最大连续子段和 | |
int sum, lmax, rmax, tmax; | |
}tree[N * 4]; | |
void pushup(Node &u, Node &l, Node &r) { | |
u.sum = l.sum + r.sum; | |
u.lmax = max(l.lmax, l.sum + r.lmax); | |
u.rmax = max(r.rmax, l.rmax + r.sum); | |
u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax); | |
} | |
void pushup(int u) { | |
pushup(tree[u], tree[u * 2], tree[u * 2 + 1]); | |
} | |
void build(int u, int l, int r) { | |
// 因为叶子节点 只有一个元素 所以四个属性都是 这个元素自己 | |
if (l == r) tree[u] = {l, r, w[r], w[r], w[r], w[r]}; | |
else { | |
//build 代码模板 | |
tree[u] = {l, r}; | |
int mid = l + r >> 1; | |
build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r); | |
// 千万不要忘记 pushup 从叶子节点回溯 把整棵树 计算出来 | |
pushup(u); | |
} | |
} | |
//u 为当前节点 修改一个节点 x 的值 为 v | |
void modify(int u, int x, int v) { | |
// 当前节点是 [x,x] 则把它的四个属性值改成 v | |
if (tree[u].l == x and tree[u].r == x) tree[u] = {x, x, v, v, v, v}; | |
else { | |
// 递归搜索 [x,x] 最后不要忘记 回溯时候 使用 pushup 把 x 向上更新 | |
int mid = tree[u].l + tree[u].r >> 1; | |
if (x <= mid) modify(u * 2, x, v); | |
else modify(u * 2 + 1, x, v); | |
pushup(u); | |
} | |
} | |
// 查询操作 模板代码 | |
Node query(int u, int l, int r) { | |
if (tree[u].l >= l and tree[u].r <= r) return tree[u]; | |
else { | |
int mid = tree[u].l + tree[u].r >> 1; | |
if (r <= mid) return query(u * 2, l, r); | |
else if (l > mid) return query(u * 2 + 1, l, r); | |
else { | |
auto left = query(u * 2, l, r); | |
auto right = query(u * 2 + 1, l, r); | |
// 注意这里的思路 返回一个节点 因此 | |
// 我们需要根据当前区间 [left,right] 构建一个(虚拟)节点 | |
Node res; | |
pushup(res, left, right); | |
return res; | |
} | |
} | |
} | |
int main() { | |
cin >> n >> m; | |
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]); | |
build(1, 1, n); // 从根节点 1 开始 初始化线段树 | |
while (m -- ) { | |
int k, x, y; | |
scanf("%d%d%d", &k, &x, &y); | |
if (k == 1) { | |
if (x > y) swap(x, y); | |
// 注意查询 和 修改 的时候 也从根节点 1 开始 | |
printf("%d\n", query(1, x, y).tmax); | |
} | |
else modify(1, x, y); | |
} | |
return 0; | |
} |
# AcWing 246. 区间最大公约数
给定一个长度为 N 的数列 A,以及 M 条指令,每条指令可能是以下两种之一:
- C l r d,表示把 A [l],A [l+1],…,A [r] 都加上 d。
- Q l r,表示询问 A [l],A [l+1],…,A [r] 的最大公约数 (GCD)。
对于每个询问,输出一个整数表示答案。输入格式
第一行两个整数 N,M。
第二行 N 个整数 A [i]。
接下来 M 行表示 M 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
N≤500000,M≤100000, 1≤A[i]≤10^18, |d|≤10^18输入样例
5 5 1 3 5 7 9 Q 1 5 C 1 5 1 Q 1 5 C 3 3 6 Q 2 4输出样例
1 2 4
# 题目描述
给出一个长度为 N 的数列 A,给出两个操作:
- 给某个区间增加一个数;
- 询问某个区间的最大公约数;
# 题目分析
本题略显麻烦,区别于前面两个题,本题的修改变成了区间修改,而非单点修改。
但是,本题的修改并不是完整的修改,而是只有增加操作,这就启发我们可以使用差分来把区间修改变成两次单点修改,这个技巧我们在 [树状数组应用] 中已经有详细介绍,并且多此使用,如果还不熟悉的同学,需要先复习下。
使用 差分 可以把 区间增加 变成 单点增加,但是这样一来,线段树节点中存储的就是差分数组了,而不再是 原数组。这会不会对计算 最大公约数造成影响呢?
要回答这个问题,我们必须先掌握最大公约数的一个性质:
gcd(a1, a2, a3, ... ,a[n]) = gcd(a1, a2-a1, a3-a2, ... , a[n]-a[n-1])
要证明这个性质,我们可以使用 A>=B 和 B>=A 推出 A=B 的方法:
对于上公式中,左边 <= 右边的情况。我们知道通过更相减损术求最大公约数有公式:
gcd(a, b)=gcd(a-b, b);所以,如果 d 是左边的最大公约数,那么 d 也一定是右边的最大公约数。对于上公式中,左边 >= 右边的情况。假设
d是右边的最大公约数,那么d一定是a1的约数,同时d也是a2-a1的约数,所以可以推出来d同样是(a2-a1)+a1=a2的约数。以此类推,d能整除左边。综上,我们可以推出上述性质。
现在,有了这个性质的加持,我们可以维护差分数组 b,求 b 的最大公约数就等价于求原数组的最大公约数。
因为求差分数组的方法是 b[i]=a[i]-a[i-1] ,所以我们可以把上一个公式再次变化为: gcd(a1, b2, b3, ... , b[n]) 。
进一步的,如果我们把这个求区间 a [1~n] 的公式扩展为求 [l,r] 的公式就变成了 gcd(a[l], b[l+1, r])
也就是说,我们只需要求出 A[l] 以及区间 b [l+1,r] 的最大公约数即可,那差分数组 b 我们是在线段树节点中动态维护的,所以直接查询即可,那么原数组中的 A [l] 要怎么求呢?其实就是使用前缀和把差分数组还原成原数组。所以,我们还需要在线段树节点中维护一个前缀和的属性。
如此,使用这种方法,我们就把区间增加,转换为两次单点修改。
总结一下就是,树状数组节点存储的数组是差分数组,我们要维护的信息有两个,一个前缀和 用来求原数组 a [l], 一个最大公约数 用来求 gcd (a [l], gcd (b [l+1, r]))。
# Code
实现上,只要抄一下线段树模板,把在 pushup 中维护最大公约数即可。
#include <cstdio> | |
#include <iostream> | |
#include <cstring> | |
#include <algorithm> | |
using namespace std; | |
const int N = 500010; | |
typedef long long LL; | |
int n, m; | |
struct Node { | |
int l, r; | |
LL sum, d; | |
}tree[N * 4]; | |
LL a[N]; | |
LL gcd(LL a, LL b) { | |
return b ? gcd(b, a % b) : a; | |
} | |
void pushup(Node &u, Node &l, Node & r) { | |
u.sum = l.sum + r.sum; // 差分的前缀和 就是区间和 | |
u.d = gcd(l.d, r.d); | |
} | |
void pushup(int u) { | |
pushup(tree[u], tree[u * 2], tree[u * 2 + 1]); | |
} | |
// 线段树模板 | |
void build(int u, int l, int r) { | |
if (l == r) { | |
LL b = a[r] - a[l - 1]; // 差分计算 | |
tree[u] = {l, l, b, b}; // 添加节点信息到叶子节点 | |
} else { | |
tree[u].l = l, tree[u].r = r; // 记录当前节点区间 忘记就会 error SF。 | |
int mid = l + r >> 1; | |
build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r); | |
pushup(u); | |
} | |
} | |
void modify(int u, int x, LL v) { | |
if (tree[u].l == x and tree[u].r == x) { | |
LL b = tree[u].sum + v; // 单点增加 | |
tree[u] = {x, x, b, b}; // 更新节点信息 | |
} else { | |
int mid = tree[u].l + tree[u].r >> 1; | |
if (x <= mid) modify(u * 2, x, v); | |
else modify(u * 2 + 1, x, v); | |
pushup(u); | |
} | |
} | |
Node query(int u, int l, int r) { | |
if (tree[u].l >= l and tree[u].r <= r) { | |
return tree[u]; | |
} else { | |
int mid = tree[u].l + tree[u].r >> 1; | |
if (r <= mid) return query(u * 2, l, r); | |
else if (l > mid) return query(u * 2 + 1, l, r); | |
else { | |
auto left = query(u * 2, l, r); | |
auto right = query(u * 2 + 1, l, r); | |
Node res; | |
pushup(res, left, right); | |
return res; | |
} | |
} | |
} | |
int main() { | |
cin >> n >> m; | |
for (int i = 1; i <= n; i ++ ) scanf("%lld", &a[i]); | |
build(1, 1, n); | |
LL d; | |
int l, r; | |
char op[2]; | |
while (m -- ) { | |
scanf("%s%d%d", op, &l, &r); | |
if (*op == 'Q') { | |
auto left = query(1, 1, l); | |
Node right({0, 0, 0, 0}); | |
if (l + 1 <= r) right = query(1, l + 1, r); | |
printf("%lld\n", abs(gcd(left.sum, right.d))); // 用公式 gcd (a [l], b [l+1, r]) 计算结果 | |
} else { | |
scanf("%lld", &d); | |
modify(1, l, d); | |
// 需要特判一下 r == n 的情况 | |
if (r + 1 <= n) modify(1, r + 1, -d); // 注意区间增加 变成 两个单点增加 | |
} | |
} | |
return 0; | |
} |
未完待续