# 前置知识

接前文：看完必会的线段树攻略 2.0（上）。

在前文中，着重讲解了线段树的单点修改和区间查询两个操作，并没有涉及到区间修改，因此在本文中将之补充。

# 线段树

简单回顾一下前文的内容。

在单点修改中，使用的方法是先找到这个元素所在的叶子节点，从叶子节点 pushup 一遍，更新它的所有祖先节点。而这个 pushup 操作，因为要从叶子节点更新到根节点，所以该操作是和树高度成正比的，因此时间复杂度是 O(logn) 。

如果延续单点修改的思路到区间修改，假设需要修改的区间有 n 个元素，那么时间复杂度将会来到 O(nlogn) ，这是非常慢的。所以线段树在做区间修改的时候需要用到一个小技巧 -- 懒标记。

# 懒标记

在区间查询中，只要发现当前搜索到的区间已经包含了需要查询的区间就可以直接返回结果。

区间修改同样可以使用类似的思路。只要当前搜索到的区间已经包含了需要修改的区间，就不再继续搜索，而是在当前搜索的区间打一个标记 add。

懒标记 add ：表示给每一个以当前节点为根的子树中的每个节点都加上 add （不包含当前节点自己）。

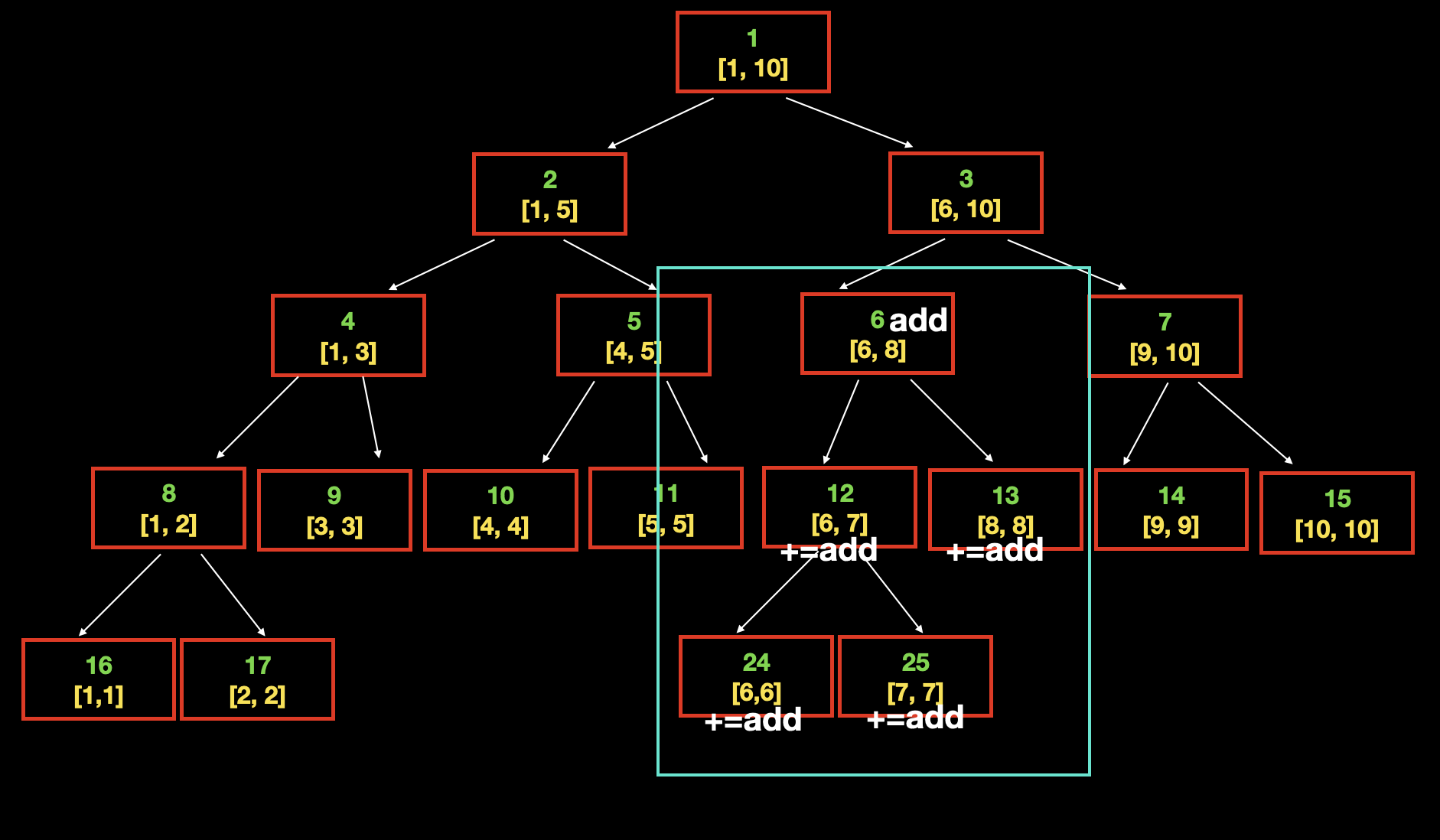
如上图所示的线段树中，我们给六号节点添加了一个标记 add，表示这个区间内的数增加了 add，但是这个标记并没有向下传播，而是在添加标记后就认为是完成了这次区间修改。如此一来，区间修改的时间复杂度变的和区间查询一致，同是 O (logn) 级别。

# 带有懒标记的查询

在使用了懒标记之后，在查询的过程中就需要计算上标记的值。

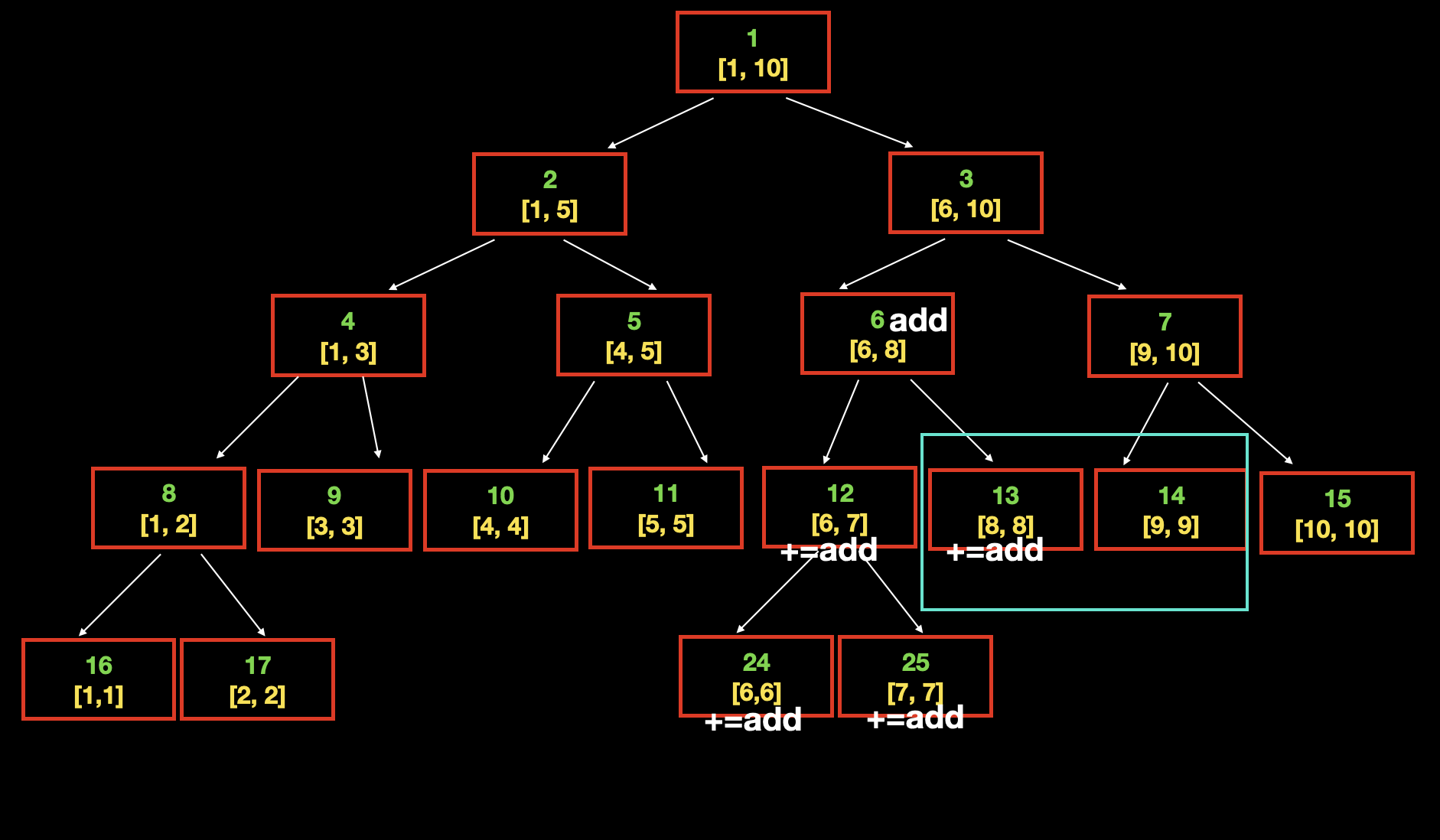
假如需要查询的区间是 [8,9] ，我们发现节点 [8,8] 的父节点上有一个 add 标记，所以在 [8,8] 上也要相应的增加 add ，那么查询的结果才能正确。

如何做到这一点呢？方法是在查询的过程中把节点上的标记向下传递并且清空，我们称这一操作为 pushdown ，也就是上一篇文章中提到的由父节点更新子节点。

举个例子，假如我们查询到了六号节点 [6,8] ，发现了它的身上有 add 标记，就把这个标记向下传递，让它的子节点 (12,13) 增加相应的值，再将六号节点上的标记清空掉。

这样就保证了在计算当前节点的时候，它的所有祖宗节点上的标记都已经累加到了当前节点。也就是说我们查询到 13 号节点的时候，它的六号父节点上的 add 标记已经计算到 13 号节点上了。

# 累加标记到子节点

假设线段树中维护的信息是区间和。

	// 父节点的标记传递到子节点
	left.add += root.add;
	// 维护子节点总和需要把子节点对应的区间内每一个数都加上 add
	left.sum += (left.R - left.L + 1) * root.add;

	// 用相同的方法把标记传到右子节点
	right.add += root.add;
	right.sum += (right.R - right.L + 1) * root.add;

	// 清空父节点的标记
	root.add = 0;

需要注意的一点是不但要在查询的时候加入 pushdown，在修改的使用同样也需要加入该操作 (pushdown)。

试想一下，如果我们给区间 [6,9] 增加了 10 之后，又要给区间 [8,9] 增加 5，假如第二次修改时，标记 10 还没有传递出去，那么会出现区间 [6,9] 一半需要加 10，一半需要加 15，造成冲突，产生错误。

# AcWing 243. 一个简单的整数问题 2

给定一个长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：
C l r d，表示把 A [l],A [l+1],…,A [r] 都加上 d。
Q l r，表示询问数列中第 l∼r 个数的和。
对于每个询问，输出一个整数表示答案。
输入格式
第一行两个整数 N,M。
第二行 N 个整数 A [i]。
接下来 M 行表示 M 条指令，每条指令的格式如题目描述所示。
输出格式
对于每个询问，输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤10^5,
|d|≤10000,
|A[i]|≤10^9
输入样例
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例
4
55
9
15

# 题目描述

给出一个长度为 N 的数列，给出两个操作：

区间增加；
区间查询；

# 题目分析

本题是一个模板题，我们先用这道题来熟悉一下带有懒标记的线段树。

线段树的代码很长，因此不好写，下面代码中两个 pushdown 的位置是需要特别关注的。

# Code

	#include <iostream>
	#include <cstring>
	#include <cstdio>
	#include <algorithm>

	using namespace std;

	typedef long long LL;

	const int N = 100010;
	int n, m;
	struct Node {
	int l, r;
	LL sum, add;
	}tree[N * 4];
	int w[N];

	// 子节点计算父节点
	void pushup(int u) {
	tree[u].sum = tree[u * 2].sum + tree[u * 2 + 1].sum;
	}

	void pushdown(int u) {
	auto &root = tree[u], &left = tree[u * 2], &right = tree[u * 2 + 1];
	if (root.add) {
	// 分析中的懒标记操作
	left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add;
	right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add;
	root.add = 0;
	}
	}

	void build(int u, int l, int r) {
	// 初始化所有叶子节点
	if (l == r) tree[u] = {l, r, w[r], 0};
	else {
	tree[u].l = l, tree[u].r = r;
	int mid = l + r >> 1; // 计算 mid
	// 递归左右
	build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r);
	pushup(u);
	}
	}

	// 区间修改
	void modify(int u, int l, int r, int v) {
	// 找到了需要修改的区间
	if (tree[u].l >= l and tree[u].r <= r) {
	// 修改该区间并且增加懒标记
	tree[u].sum += (tree[u].r - tree[u].l + 1) * v;
	tree[u].add += v;
	} else {
	// 注意此处必须优先 pushdown
	pushdown(u);
	int mid = tree[u].l + tree[u].r >> 1;
	if (l <= mid) modify(u * 2, l, r, v);
	if (r > mid) modify(u * 2 + 1, l, r, v);
	// 注意此处必须 pushup
	pushup(u);
	}
	}

	LL query(int u, int l, int r) {
	if (tree[u].l >= l and tree[u].r <= r) return tree[u].sum;
	// 注意此处必须优先 pushdown
	pushdown(u);
	int mid = tree[u].l + tree[u].r >> 1;
	LL sum = 0;
	// 计算查询区间的总和
	if (l <= mid) sum = query(u * 2, l, r);
	if (r > mid) sum += query(u * 2 + 1, l, r);
	return sum;
	}

	int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
	build(1, 1, n);
	char op[2];
	int l, r, v;
	while (m -- ) {
	scanf("%s%d%d", op, &l, &r);
	if (*op == 'C') {
	scanf("%d", &v);
	modify(1, l, r, v);
	} else printf("%lld\n", query(1, l, r));
	}
	return 0;
	}

# AcWing 1277. 维护序列

老师交给小可可一个维护数列的任务，现在小可可希望你来帮他完成。
有长为 N 的数列，不妨设为 a1,a2,…,aN。
有如下三种操作形式：
把数列中的一段数全部乘一个值；
把数列中的一段数全部加一个值；
询问数列中的一段数的和，由于答案可能很大，你只需输出这个数模 P 的值。
输入格式
第一行两个整数 N 和 P；
第二行含有 N 个非负整数，从左到右依次为 a1,a2,…,aN；
第三行有一个整数 M，表示操作总数；
从第四行开始每行描述一个操作，输入的操作有以下三种形式：
1 t g c ，表示把所有满足 t≤i≤g 的 ai 改为 ai×c；
2 t g c ，表示把所有满足 t≤i≤g 的 ai 改为 ai+c；
3 t g ，询问所有满足 t≤i≤g 的 ai 的和模 P 的值。
同一行相邻两数之间用一个空格隔开，每行开头和末尾没有多余空格。
输出格式
对每个操作 3，按照它在输入中出现的顺序，依次输出一行一个整数表示询问结果。
数据范围
1≤N,M≤10^5,
1≤t≤g≤N,
0≤c,ai≤10^9,
1≤P≤10^9
输入样例
7 43
1 2 3 4 5 6 7
5
1 2 5 5
3 2 4
2 3 7 9
3 1 3
3 4 7
输出样例
2
35
8

# 题目描述

与上题相似，同样是给出一个序列，进行操作，本题有三种操作方式：

给某段区间 [l,r] 增加一个数；
给某段区间 [l,r] 乘以一个数；
查询某段区间的和；

# 题目分析

标准的线段树模板题。

要思考的第一个问题是如何既能计算加法又能计算乘法呢？

可以考虑使用两个懒标记，一个表示加法，一个表示乘法。

如此，本题就变成了标准的线段树模板，只是在 pushdown 里面，我们需要维护两个懒标记。

既然是两个懒标记，就会出现计算顺序的问题，考虑下面的问题：

对于给出线段树，我们执行三个操作：

对区间 [1,2,3] 进行 +3；
对区间 [1,2,3] 进行 *3；
对区间 [1,2,3] 进行 +3；

也就是我们的标记变化为：

add += 3, sum += ((3-1)+1)*3 ，其中 sum 表示题目求的区间和；
mult *= 3 ；
add += 3 ；

那么问题来了，操作 2 执行之后，sum 的值是： (a[1]+3)*3 + (a[2]+3)*3 + (a[3]+3)*3

到了操作 3 之后，因为 add 标记只有一个，所以再加 3 会变成：

(a[1]+3+3)*3 + (a[2]+3+3)*3 + (a[3]+3+3)*3

也就是两个 + 3 共同组成了 add 标记，但是这样显然是不对的，因为我们期待的公式是这样的：

(a[1]+3)*3+3 + (a[2]+3)*3+3 + (a[3]+3)*3+3

为什么会出现这种情况呢？因为我们一次计算中，同时计算了两个标记，这两个标记是没有先后顺序的。

那么，如何避免这种矛盾出现呢？很简单，对于标记的计算遵守先乘后加的原则。也就是说，我们让操作 2 计算之后变成这样：

a[1]*3+3 + a[2]*3+3 + a[3]*3+3

如此，当执行操作 3，计算第二个 +3 的时候，公式就会变成我们期待的样子：

a[1]*3+3+3 + a[2]*3+3+3 + a[3]*3+3+3

# Code

在实现上还有一个小细节需要注意，add 标记的初始值是 0，而 mult 的初始值不能是 0，需要设置成 1，因为 0 会把所有和它想乘的，都变成 0。

	#include <iostream>
	#include <cstring>
	#include <algorithm>

	using namespace std;

	typedef long long LL;

	const int N = 100010;
	struct Node {
	int l, r;
	int add, mult, sum; // 加法标记乘法标记区间和
	}tree[N * 4];
	int n, m, P;
	int w[N];

	// 我们把更新操作单独拿出来因为在修改指定区间的时候
	// 需要单独做一次修改（不使用 pushdown）
	void eval(Node &u, int add, int mult) {
	// 修改一段区间乘法直接用区间和乘以标记 mult
	// 加法需要让区间 [l,r] 中所有元素都加上标记 add
	u.sum = ((LL)u.sum * mult + (LL)(u.r - u.l + 1) * add) % P;
	u.mult = (LL)u.mult * mult % P; // 乘法更新标记
	u.add = ((LL)u.add * mult + add) % P; // 加法更新标记注意先乘后加规则
	}

	// 父节点计算两个子节点
	void pushdown(int u) {
	// 计算两个子节点并清空当前节点
	eval(tree[u * 2], tree[u].add, tree[u].mult);
	eval(tree[u * 2 + 1], tree[u].add, tree[u].mult);
	tree[u].add = 0;
	tree[u].mult = 1;
	}

	// 子节点区间和计算父节点区间和
	void pushup(int u) {
	tree[u].sum = (tree[u * 2].sum + tree[u * 2 + 1].sum) % P;
	}

	// 建树模板
	void build(int u, int l, int r) {
	if (l == r) tree[u] = {l, r, 0, 1, w[l]}; // 注意这里乘法标记初始化是 1
	else {
	tree[u] = {l, r, 0, 1, 0};
	int mid = l + r >> 1;
	build(u * 2, l, mid), build(u * 2 + 1, mid + 1, r);
	pushup(u);
	}
	}

	// 修改模板
	void modify(int u, int l, int r, int add, int mult) {
	// 找到指定的修改区间进行一次计算修改掉指定区间的值并且更新标记
	if (l <= tree[u].l and tree[u].r <= r) eval(tree[u], add, mult);
	else {
	pushdown(u); // 注意 pushdown 的位置
	int mid = tree[u].l + tree[u].r >> 1;
	if (l <= mid) modify(u * 2, l, r, add, mult);
	if (r > mid) modify(u * 2 + 1, l, r, add, mult);
	pushup(u); // 注意 pushup 的位置
	}
	}

	// 查询模板
	int query(int u, int l, int r) {
	if (l <= tree[u].l and tree[u].r <= r) return tree[u].sum;
	else {
	pushdown(u); // 注意 pushdown 的位置
	int mid = tree[u].l + tree[u].r >> 1;
	int res = 0;
	if (l <= mid) res = query(u * 2, l, r);
	if (r > mid) res = (res + query(u * 2 + 1, l, r)) % P;
	return res;
	}
	}

	int main() {
	cin >> n >> P;
	for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
	build(1, 1, n);
	cin >> m;
	while (m -- ) {
	int t, l, r, c;
	scanf("%d%d%d", &t, &l, &r);
	if (t == 1) {
	scanf("%d", &c);
	modify(1, l, r, 0, c);
	} else if (t == 2) {
	scanf("%d", &c);
	modify(1, l, r, c, 1);
	} else printf("%d\n", query(1, l, r));
	}
	return 0;
	}

# 总结

线段树的入门攻略，目前预计总共就这两篇文章，除开基本讲解外总共五道题。

总体来讲，难度还是超过了预期的，但是仍然有迹可循，整个模板的大部分代码都是固定的，最大的难点在于细节的处理以及 pushdown 和 pushup 的计算。

因此，使用线段树的时候，可以按照下面的顺序思考：

线段树节点里维护的主要信息是什么？维护该信息的计算时候，是否需要额外的辅助属性也存储在节点中？
计算节点信息的方法？计算 pushdown 和 pushup 的方法？计算的时候是否需要使用 long long ？
修改和查询的时候必须注意 pushdown 和 pushup 的位置。
背熟模板代码，起码在模板部分不要出错误。

END

经典必会 AcWing算法提高课线段树

# 前置知识

# 线段树

# 懒标记

# 带有懒标记的查询

# 累加标记到子节点

# AcWing 243. 一个简单的整数问题 2

# 题目描述

# 题目分析

# Code

# AcWing 1277. 维护序列

# 题目描述

# 题目分析

# Code

# 总结

看完必会的线段树攻略2.0（上）

看完必会的字典树攻略