前置知识:并查集,今天的这个题目的做法是并查集的进阶操作,因此必须先熟练应用并查集,并且懂得原理。
题目链接:https://www.acwing.com/problem/content/242/
参考视频题解:https://www.acwing.com/video/251/
# 题目详情
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形。
A 吃 B,B 吃 C,C 吃 A。
现有 N 个动物,以 1∼N 编号。
每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X 和 Y 是同类。
第二种说法是 2 X Y,表示 X 吃 Y。
此人对 N 个动物,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
当前的话与前面的某些真的话冲突,就是假话;
当前的话中 X 或 Y 比 N 大,就是假话;
当前的话表示 X 吃 X,就是假话。
你的任务是根据给定的 N 和 K 句话,输出假话的总数。输入格式
第一行是两个整数 N 和 K,以一个空格分隔。以下 K 行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中 D 表示说法的种类。
若 D=1,则表示 X 和 Y 是同类。
若 D=2,则表示 X 吃 Y。
输出格式
只有一个整数,表示假话的数目。数据范围
1≤N≤50000,
0≤K≤100000输入样例:
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出样例:
3
# 并查集基础
这里简单回顾一下并查集的理论基础。并查集,人如其名,共有两个方法,一并一查,主要作用是判断哪些元素在同一个集合,我们初始化所有的元素都单独占用一个集合,在知道某两个元素属于同类后,把它俩合并到其中一个集合,这样经过数次合并,我们就可以把相同元素放到同一个集合中。
而本题则需要使用带权重的并查集。
# 题意解读
先来看下题意,明确题意是非常重要的。
在动物王国里面有三个动物,他们的克制关系,构成了环形。A->B->C->A。 对于每一个动物,我们都不知道它属于 {A,B,C} 的哪一种,有人用两种说法来描述 N 个动物:1. 使用 1 X Y 表示 X 和 Y 是同一种动物; 2. 使用 2 X Y 表示 X 可以吃掉 Y。
此人对这 N 个动物,一句接一句的说出 K 句话,问我们 K 句话的真假,最后要求 输出假话的总数。
其中假话的规则是:
- 当前的话与前面的某些真话冲突;
- 当前的话中 X 或者 Y 比 N 还大;
- 当前的话表示 X 吃 X。
满足以上任意一条,则是假话,否则便认为是真话。
看一下样例的意思:
- 样例第一行,表示
N=100,K=7; - 后面 7 行,表示这个人说了 7 句话;
- 第一句话
1 101 1,其中 X 的值比 N 还大,命中了假话规则的第二条,所以是假话; - 第二句话
2 1 2,表示 1 号动物可以吃掉 2 号动物,未命中任意假话规则,所以是真话; - 第三句话
2 2 3,表示 2 号动物可以吃掉 3 号动物,未命中任意假话规则,所以是真话; - 第四句话
2 3 3,表示 3 号动物可以吃掉 3 号动物,显然命中了第三条假话规则,所以是假话; - 第五句话
1 1 3,表示 1 号动物与 3 号动物是同类,根据第二句话 1 吃 2,以及第三句话 2 吃 3,并且他们具有环形克制关系,我们知道 3 吃 1,所以 1 和 3 是同类,是假话。 - 第六句话
2 3 1,表示 3 号动物吃 1 号动物,根据第五句话的分析,我们知道是真话; - 第七句话
1 5 5,表示 5 号动物和 5 号动物是同类,所以是真话。 - 也就是说,这七句话中,有第 1 句,第 4 句,第 5 句,共三句话是假话,所以最后输出 3.
# 分析及实现
如果你熟悉并查集就会发现:只要两个动物之间存在关系,我们就可以把他们放到一个集合。
为什么这样呢?因为动物之间的相互关系是环形的,所以一个集合内的动物关系是确定的,即便不知道也能推理出来。
举个例子:我们知道 A 和 B 有关系,把他们放在一个集合;又知道了 B 和 C 有关系,那把 C 也加入到这个集合,此时,我们也能推理出来 A 和 C 的关系:
- 如果 A 和 B 同类,B 和 C 同类,则 A 和 C 同类;
- 如果 A 和 B 同类,B 吃 C,则 A 也吃 C;
- 如果 A 吃 B,B 吃 C,则 C 吃 A;
- 如果 A 吃 B,B 和 C 同类,则 A 吃 C;
也就是说,不管两个动物是同类还是被吃,把他们放到集合里就一定能知道他们的关系。
那么,我们如何能知道他们之间的关系呢? (这是本题最最关键的问题,也是最大的难点。)
使用的方法是记录集合中的每一个点 与 根节点 之间的关系。 我们用每个点到根节点的距离,表示每个点 与 根节点的关系。
我们规定:
- 某点 (A) 到根节点的距离模 3 余 1,表示它可以吃根节点;
- 某点 (B) 到根节点的距离模 3 余 2,表示它被根节点吃;
- 某点 (C) 到根节点的距离模 3 余 0,表示它与根节点是同类;
因为只有三种动物,所以其中 到根节点的距离 是对 3 取模的结果。
如此,所有取模余 1,表示它吃根节点;取模余 2 表示根节点吃它;那么根据环形关系,我们就知道余 2 的点可以吃掉余 1 的点。
那么,每个点到根节点初始的距离应该如何得出来呢?其实就是当我们遇到两个节点的关系是 “吃与被吃” 时,“吃” 的点到根节点的距离即为 “被吃” 点到根节点距离加 1。
举个例子,如果当前 x 吃 y,那么 y 就是第 0 类动物,x 是第 1 类动物;z 吃 x,那么 z 就是第 2 类动物,所以第 0 类动物可以吃掉 z;则他们三个的关系如下图所示: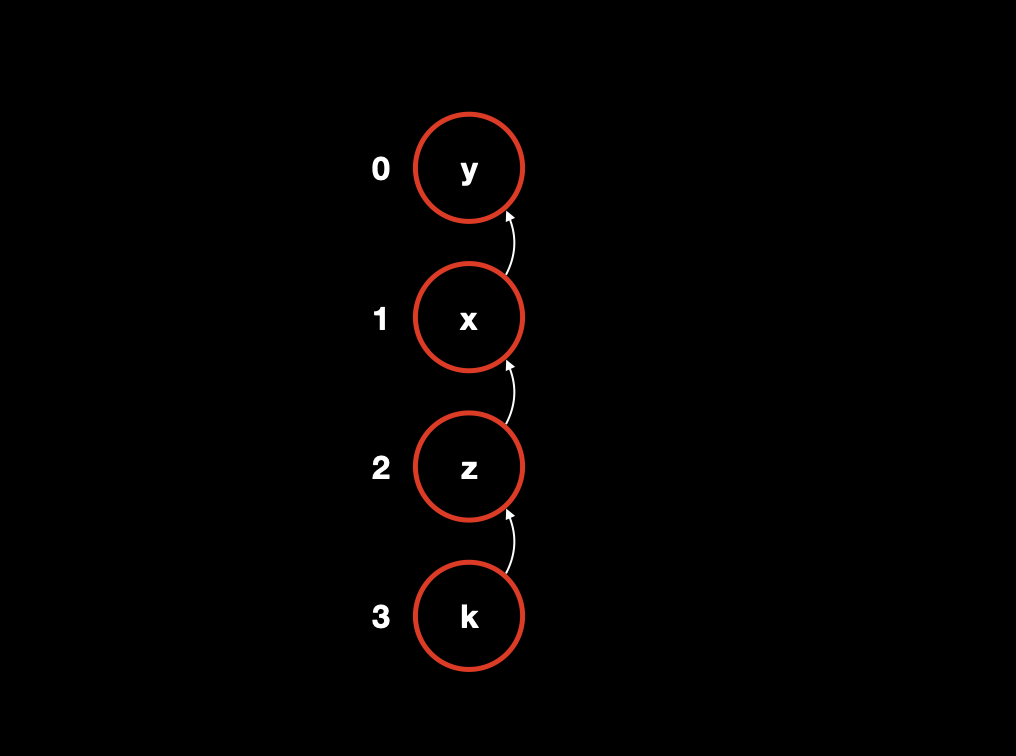
从图中我们可以看出,根据上面我们定的规则:
- 点 x 到根节点的距离为 1,因此它模 3 余 1,则表示它吃根节点;
- 点 z 到根节点的距离为 2,因此它模 3 余 2,则表示他被根节点吃;
- 点 k 到根节点的距离为 3,因此它模 3 余 0,则表示它与根节点同类;
- 也因此,z 到 k 的距离为 1,用来表示 k 吃 z。
注意我们规则里最重要的一点:被吃的在前面,吃它的在后面。即,x 吃 y 表示为 y 到 x 的距离为 1,y 在上,x 在下。
(至此,请各位读者大大,务必理解上面的表示形式,以及 集合中的点的含义,以及 这些点之间的关系是如何确定的。)
OK,明确了上面的表示形式之后,我们又发现一个问题,即,根据上面的分析,我们似乎只能知道每个点到父节点的距离,那么如何知道每个点到根节点的距离呢?
只要在路径压缩的时候,把每个点到根节点的距离 计算出来 就可以了。因为在路径压缩之后,它的父节点就是它的根节点。(不理解路径压缩,请看前置文章:并查集)
# Code
初始化数据,n 表示总共有多少动物,m 表示总共有多少句话,即读入的第一行数据。p 表示并查集的集合,d 表示存储当前节点到父节点的距离(注意路径压缩后父节点与根节点是重合的)。
#include <iostream>using namespace std;
const int N = 50010;
int n, m;
int p[N], d[N];
并查集的 find 函数,在普通 find 函数中,我们一般会完成路径压缩,而在上面的分析中也已经提到了在路径压缩的时候会做一件事情:计算出所有节点到父节点的距离。
具体的,只要使用 x 到父节点的距离,加上父节点到根节点的距离即可。但是这里面有两个坑:
我们很容易写出这样的代码,即,先路径压缩,然后计算距离:
p[x] = find(p[x]);
d[x] += d[p[x]];
这样写就上当了,仔细看,此时在执行第二行计算距离的时候 p [x] 已经变成根节点了,而 d 中存的是当前点到父节点的距离。
那,先计算距离,再递归行不行呢?比如这样:
d[x] += d[p[x]];
p[x] = find(p[x]);
这样其实也不行,因为现在 d [p [x]] 存储的还是 p [x] 到父节点的距离,而没有存储父节点到根节点的距离,我们必须使用自底向上的递归,即先递归
find(p[x]),然后再从根节点反向计算。
int find(int x) {
if (p[x] != x) {
int t = find(p[x]);
d[x] += d[p[x]];
p[x] = t;
}return p[x];
}触发假话条件 1.
if (x > n || y > n) res ++ ;
如果当前的 x 和 y 是同类的处理方式。当遇到有关系的 x 和 y 之后,必要的判断是他们在不在一个集合,如果不在要把他们合并到一个集合。其次,如果是同类的话,根据我们上面的规则,必有 d [x]%3==d [y]%3。 根据同余定理,也可以写成
(d[x]-d[y])%3==0。为什么有这个等式?参考一下前面的分析,我们用
到根节点距离 模3取余来表示一个动物是哪个种类,而 d 保存的是该点到父节点的距离,经过路径压缩之后它的父节点也是它的根节点,所以上面等式成立。(后面写为根(父)节点,以作提示。)px = find(x), py = find(y);
//t = 1 表示 xy 同类。if (t == 1) {
if (px == py && (d[x] - d[y]) % 3) res ++ ;
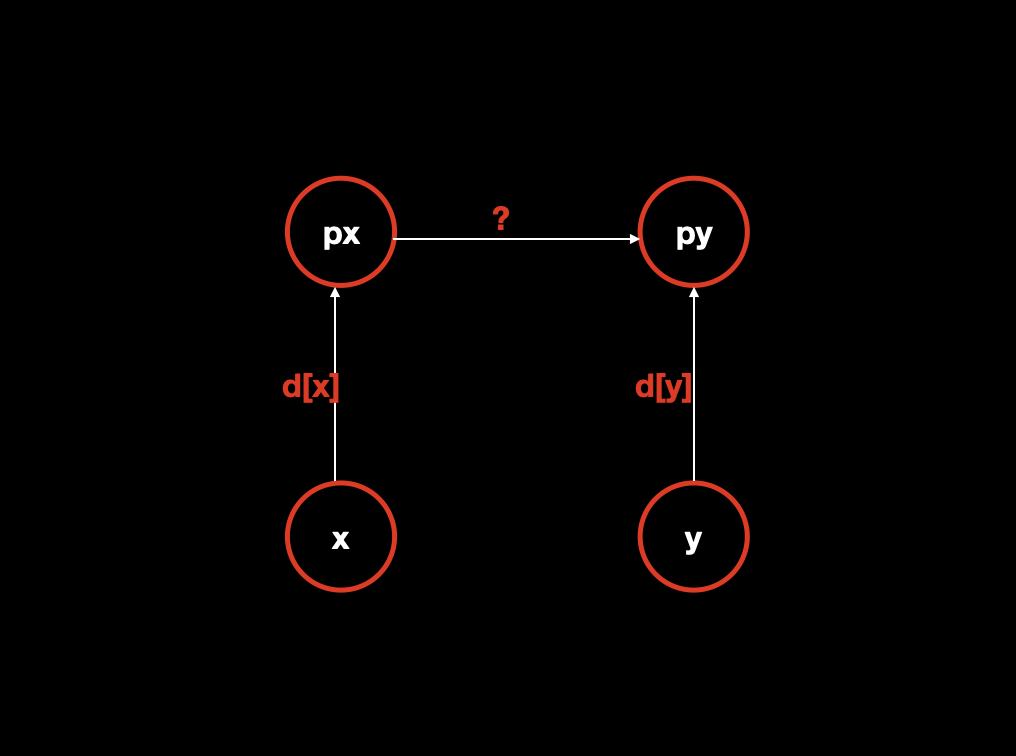
}如果 x 和 y 不在同一集合,且 x 与 y 同类,要如何把他们合并到一起呢?或者说难点在于合并的时候,距离要如何计算呢?
![]()
如图所示,连接 px 和 py 之前,他们分别属于两个集合,而 x 到 px 和 y 到 py 是已经知道的,所以当连接之后?即是我们要求的,当 x 和 y 同类的时候,我们可以得到(d[x] + ? - d[y]) % 3 == 0,因为 x 和 y 是同类,所以 x 到根 (父) 节点的距离(d [x] + ?)和 y 到根 (父) 节点的距离(d [y])应该符合我们步骤四中推出来的等式。那么让这个等式成立,只要让d[x] + ? - d[y] == 0即可,也就是?=d[px]=d[y]-d[x]。if (px != py) {
p[px] = py;
d[px] = d[y] - d[x];
}当 x 与 y 在一个集合,但是有
x吃y的关系的时候,我们知道 x 在 y 的下面,x 到根 (父) 节点的距离,比 y 到根 (父) 节点的距离 模 3 多 1,也就是说(d[x] - 1) % 3应该与d[y] % 3是相等的,那么根据步骤四的分析,我们就能得到(d[x] - 1 - d[y]) % 3 == 0。px = find(x), py = find(y);
//t = 2 表示 x 吃 y。if (t == 2) {
if (px == py && (d[x] - 1 - d[y]) % 3) res ++ ;
}如果 x 和 y 不在同一集合,且 x 吃 y,要如何合并他们呢?根据步骤五的分析,其实直接就能推断出来
d[x] + ? - 1 - d[y] == 0,也就是说?=d[px]=d[y] + 1 - d[x]。if (px != py) {
p[px] = py;
d[px] = d[y] + 1 - d[x];
}
将上面的所有步骤组合起来,就可以得到完整的实现啦~
#include <iostream> | |
using namespace std; | |
const int N = 50010; | |
int n, m; | |
int p[N], d[N]; | |
// 并查集 find 函数 | |
int find(int x) { | |
if (p[x] != x) { | |
int t = find(p[x]); | |
d[x] += d[p[x]]; | |
p[x] = t; | |
} | |
return p[x]; | |
} | |
int main() { | |
scanf("%d%d", &n, &m); | |
for (int i = 1; i <= n; i ++ ) p[i] = i; | |
int res = 0; | |
while (m -- ) { | |
int t, x, y; | |
scanf("%d%d%d", &t, &x, &y); | |
if (x > n || y > n) res ++ ; | |
else { | |
int px = find(x), py = find(y); | |
if (t == 1) { | |
if (px == py && (d[x] - d[y]) % 3) res ++ ; | |
else if (px != py) { | |
p[px] = py; | |
d[px] = d[y] - d[x]; | |
} | |
} | |
else { | |
if (px == py && (d[x] - d[y] - 1) % 3) res ++; | |
else if (px != py) { | |
p[px] = py; | |
d[px] = d[y] + 1 - d[x]; | |
} | |
} | |
} | |
} | |
printf("%d\n", res); | |
return 0; | |
} |
END