# AcWing 898. 数字三角形

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。
        7
      3   8
    8   1   0
  2   7   4   4    
4   5   2   6   5
输入格式
第一行包含整数 n，表示数字三角形的层数。
接下来 n 行，每行包含若干整数，其中第 i 行表示数字三角形第 i 层包含的整数。
输出格式
输出一个整数，表示最大的路径数字和。
数据范围
1 ≤ n ≤ 500,
−10000 ≤ 三角形中的整数 ≤ 10000
输入样例
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出样例
30

# 题目分析

本题是动态规划的入门题（梦开始的地方），也是 线性 动态规划中比较有代表性的题目。

# 先简单看一下题意

本题给出一个三角形的数字塔，要求从顶部走到最下方，找出 和最大 的路径，走的时候，只能走到当前节点本身的左子节点或者右子节点。

在示例中的最大路径则是： 7 -> 3 -> 8 -> 7 -> 5 ，最终得到的 路径和 是 30 。

# 处理流程分析

动态规划按照计算顺序分析，可以分为 自下到上 和 自上到下 两种。

我们看下本题，如果采用 自上到下 的方式会出现一个问题。既，需要处理边界。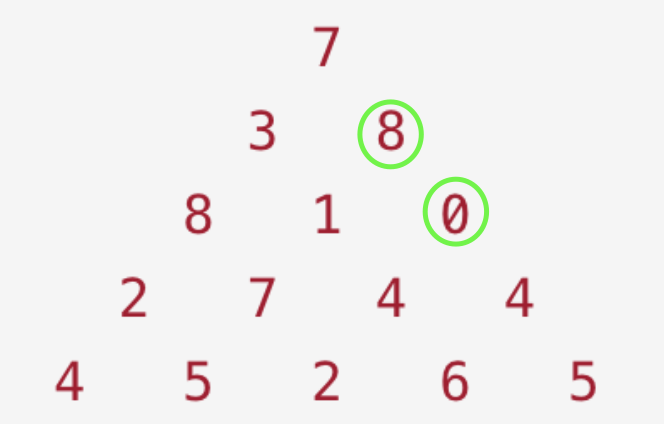

对于图中绿色节点，如果是 自上到下 的处理，我们只知道 节点0 可以从 左上方的节点8 转移过来，而不能从 右上方的不存在的节点 转移过来，因此就需要做特殊处理。

但是如果是自下向上的处理，则不会有此问题，因此 节点8 即可以由 左下方的节点1 转移过来，又可以由 右下方的节点0 转移过来。

# 动态规划

使用动态规划可以分为两个大步骤： 状态定义 与 状态计算 。

在状态定义部分，使用两个概念来组成一个状态。（把抽象的状态实例化）

状态的集合 。既，动态规划可以一次解决一类问题，我们把这个问题称为集合。
集合的属性 。既，状态一定要表示集合的某种属性，才能有意义，比如：最大值、最小值、个数等等。

在状态计算部分，其实也就是分析如何划分集合。

回到我们当前正在做的这道题。我们发现本题求的是所有路径中路径 和最大 的那条路径。因此，我们可以如下定义状态：

状态定义：用 f (i, j) 表示从下往上走，走到点 [i, j] 时候路径和最大是多少。

那么，如何划分集合呢？分析题目，我们可以发现，当前的状态 f(i, j) ，可以由左下方和右下方转移而来。

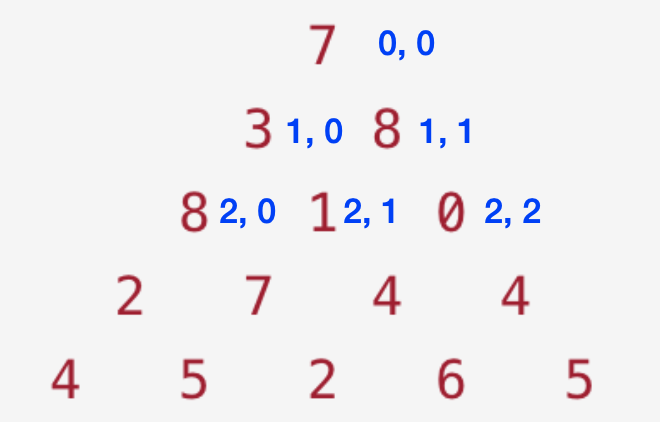
坐标示意图

从图中可以明显的看出，左下方坐标是 (i + 1, j) ，右下方坐标是 (i + 1, j + 1) 。

那么我们就可以把集合划分为两部分，一部分是 由左下方转移而来 ，对应状态定义 f(i + 1, j) ；另一部分是 由右下方转移而来 ，对应状态是 f(i + 1, j + 1) 。

注意，这两个左右状态就是自下向上到它们各自代表点所表示的最大路径和。我们知道当前所在点 [i, j] 的值是固定的，而当前状态又只能由他们两个转换而来，所以他们两个的状态中最大的那个加上当前点就形成了当前状态。

# Code

	n = int(input())
	f = [[0] * (n + 1) for _ in range(n + 10)]
	g = [[]]
	for i in range(n):
	line = list(map(int, input().split()))
	g.append(line)

	for i in range(n, 0, -1):
	for j in range(i):
	f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + g[i][j]

	print(f[1][0])

经典必会基础模板题数字三角形 AcWing算法基础课