本文参考:https://www.acwing.com/video/371/
书接上回
- 完全背包,需掌握如何推导出最终解法。
- 数据范围较小的多重背包,需掌握朴素版本解法(状态定义、状态转移),以及二进制优化版的解法。
- 滑动窗口,需熟悉概念,并且能灵活应用到对应场景。
# 多重背包问题
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 件,每件体积是 ,价值是 。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
数据范围:
题目中,主要需要关注的是数据范围。一般情况,我们会根据数据范围选择不同的解法。而本题 ( 多重背包 ) 在数据范围较小的情况,可以选择不同的解法(具体请参考前置文章):
- ,那么使用朴素版本的解法,时间复杂度为,完全 OK。
- ,此时再使用朴素版的解法时间复杂度将会来到,将会超时,因此,需要使用二进制优化,将时间复杂度优化到。
- 来到本文的数据范围,则二进制优化的时间复杂度也会超时,因此我们必须找出一种新的做法。
# 完全背包简单回顾
完全背包与多重背包
仅有一个差异:完全背包问题中的物品是可以无限选择的,而多重背包的物品是有限定数量的。也就是说多重背包和完全背包是非常相似的。完全背包中,我们使用如下的方式完成状态转移:
![]()
在完全背包中,我们的做法是用下面部分替换了上面部分,因为在完全背包中,下面部分的最大值仅比上面部分缺少一个 w,而 f [i,j-v] 表示下面红框中的最大值,那么它加上 w,就得到了上面红框部分的最大值,所以可以做等价替换,既 x = max(a, b, c), y = max(a, b, c, d) ,那么我们可以得到 y = max(x, d) ,进一步的, x 中 (a,b,c) 都比 y 中的 (a,b,c) 少一个 w ,那么 最大值x 加上这个 w 就等价与 y 中 (a,b,c) 的最大值。
# 优化多重背包
根据上节中完全背包的状态转移方式,我们很容易想到在多重背包中也使用相同的方法。所以同样来对比一下 f[i, j] 和 f[i, j-v] 。
与完全背包中的优化公式有所不同,在多重背包中 f(i,j-v) 里面多出来了一项,就会导致一个问题:已知粉色部分的最大值和红色部分,但是这并不能推出来整体的蓝色部分的最大值。
如果红色部分与粉色部分最大值相等,那么我们可以知道粉色最大值既整体的蓝色最大值,但是如果不等,我们就没法确定整体最大值,也就不能去替换黄色部分的公式,所以多重背包需要找到其他的优化方式。
我们继续往下考虑,把背包体积使用到极限。
观察上图红色部分,可以发现一个重要规律,既:红色部分 j、j-v、j-2v、... 对 v 取模的余数都相同。所以,我们假设它们对 v 取模的余数是 r。
然后,我们在数轴上从小到大,把 r 表示出来,也就是上图中的红色部分用 r 表示,同样把所有体积都使用到极限(也就是不能在装当前物品)。

那么,此时会出现一个问题:因为当前体积为 v 的物品是有数量限制的,所以可能当前物品并不能装满背包,也就是数轴中并不一定能走到左端点。
例如:当前物品只有 3 个,体积为 4,而背包总容量为 100。那么可能在中途就没有物品可以使用了。
但是,这个问题不影响我们分析,所以直接忽略该问题即可。
# 小结
现在,再明确一下目标,我们是要通过状态转移,求出 f (i,j),即,当前状态。在完全背包中,我们用 x=max(a,b,c),y=max(a,b,c,d) 可以等价变换为 y=max(x,d) 的原理,通过 f(i,j-v) 转移到 f(i,j) 。
但是,因为多重背包中 x 里面多出来的一项,即, x=max(a,b,c,q) ,导致了原理失效,所以不能在从 f(i,j-v) 转移过来,以至于我们需要寻找新的思路。
新思路中,我们用状态定义中的第二维 j,对当前物品体积 v 的取模 r,表示出了 f (i,j),f (i,j-v),f (i,j-2v),...,f (i,r+v),f (i,r)。
# 使用滑动窗口维护状态
在上面的分析中,我们已经知道了 f (i,j) 其实求的是 j-v、j-2v、...、j-sv 的最大值。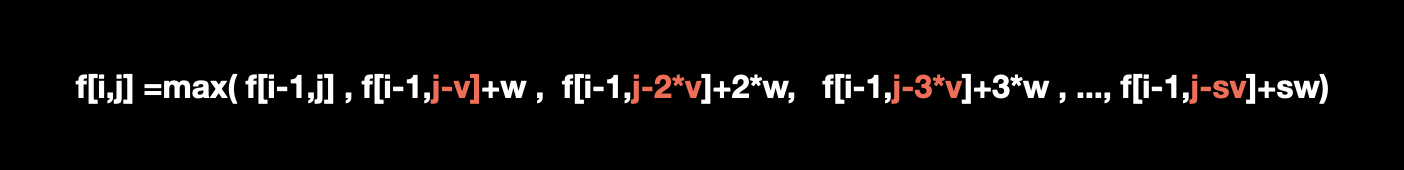
我们在数轴上看一下他们的位置:
也就是说当我们求 f(i,j) 的时候就是在求他前面 s 个数的最大值(加上偏移量 w)。
所以同理我们可知,当我们求 f(i,j-v) 的时候也是在求他前面 s 个数的最大值。
以此类推,我们惊奇的发现,这竟然是一个滑动窗口的模型。
那么,我们就可以用滑动窗口来维护大小为 s 的滑动窗口的最大值。那么, f[i, j] 就可以写成 max(f[i,j], 窗口中最大值) 。
# Code
#include <iostream> | |
#include <algorithm> | |
#include <cstring> | |
using namespace std; | |
const int N = 1010, M = 20010; | |
int n, m; | |
int f[N][M], q[M]; | |
int main() { | |
cin >> n >> m; | |
for (int i = 1; i <= n; i ++ ) { | |
int v, w, s; | |
cin >> v >> w >> s; | |
// 枚举余数 j,也就是分析中的 r | |
// 为什么枚举 r?因为枚举 r 就可以求出所有的 f [i,0]~f [i,m] | |
// 比如想枚举 f [i,0]~f [i,11] 也就是 0~11,而物品体积 v 为 3 | |
// 可以枚举余数(0,1,2)。 | |
// 组成 {0,3,6,9}、{1,4,7,11}、{2,5,8,12} 来表示(0~11)。 | |
for (int r = 0; r < v; r ++ ) { | |
int hh = 0, tt = -1; // 定义队列,hh 表示队头,tt 表示队尾 | |
// 枚举体积 | |
for (int j = r; j <= m; j += v) { | |
// 滑动窗口的大小为 s,j 是当前选择的背包体积, | |
// 如果 j 超过了当前物品能选择的总体积 (数量 s * 单位体积 v), | |
// 说明窗口滑出,则将队头元素踢出窗口。 | |
if (hh <= tt && q[hh] < j - s * v) hh ++; | |
f[i][j] = f[i - 1][j]; // 不放物品 i | |
// 其中队头,既 q [hh] 保存的就是分析中的最大值,也就是 max (j-v,j-2v,j-3v...) | |
// 假设 q [hh] 是 j-2v ,那么 j-q [hh] 就等价于 j-(j-2v)=2v 再除以 v 就得出来最大值时候选择的物品数量 | |
// 再 乘以 w 就是 最大值时候的价值。所以 (j-q [hh]) /v * w 表示的就是分析中的偏移量 w。 | |
if (hh <= tt) f[i][j] = max(f[i][j], f[i - 1][q[hh]] + (j - q[hh]) / v * w); | |
// 维持单调性。 由上一层 i-1 转移过来,判断价值是否超过了队尾元素。 | |
//f [i - 1][q [tt]] + (j - q [tt]) /v * w 同上一句代码类似,表示队尾元素的价值。 | |
while (hh <= tt && f[i - 1][q[tt]] + (j - q[tt]) / v * w <= f[i - 1][j]) tt -- ; | |
// 加入到队列。 | |
q[ ++ tt] = j; | |
} | |
} | |
} | |
cout << f[n][m] << endl; | |
return 0; | |
} |
用滚动数组将代码优化成一维。
#include <iostream> | |
#include <algorithm> | |
#include <cstring> | |
using namespace std; | |
const int N = 20010; | |
int n, m; | |
int f[N], g[N], q[N]; | |
int main() { | |
cin >> n >> m; | |
for (int i = 0; i < n; i ++ ) { | |
int v, w, s; | |
cin >> v >> w >> s; | |
memcpy(g, f, sizeof f); | |
for (int j = 0; j < v; j ++ ) { | |
int hh = 0, tt = -1; | |
for (int k = j; k <= m; k += v ) { | |
if (hh <= tt && q[hh] < k - s * v) hh ++ ; | |
if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w); | |
while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt --; | |
q[ ++ tt] = k; | |
} | |
} | |
} | |
cout << f[m] << endl; | |
return 0; | |
} |
END
